 |
Построение и анализ ЛЧХ системы и годографа Найквиста скорректированной системы
|
|
|
|
Анализ устойчивости замкнутой системы
Анализ устойчивости системы по корням характеристического уравнения
Запишем передаточную функцию разомкнутой системы:
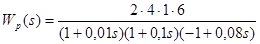 . (1)
. (1)
Передаточная функция замкнутой системы имеет вид:
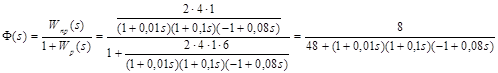 .
.
Характеристическое уравнение замкнутой системы:
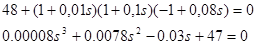 (2)
(2)
Корни характеристического уравнения (2):
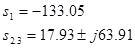
Характеристическое уравнение (2) имеет два правых корня, следовательно, данная замкнутая система неустойчива.
Анализ устойчивости системы по алгебраическому критерию
Для характеристического уравнения (2) замкнутой системы коэффициенты ai, i =0..3,
а0=0.00008,
a 1 =0.0078,
a 2 = – 0.03,
a 3 =48.
Необходимым условием устойчивости системы является:
ai >0, i =0..3
Данное условие не выполняется (a 2 <0), следовательно, замкнутая система неустойчива.
Анализ устойчивости системы по частотным критериям
А) Критерий Найквиста (на комплексной плоскости)
Используя передаточную функцию разомкнутой системы (1) запишем характеристическое уравнение разомкнутой системы:
 . (3)
. (3)
Найдем корни характеристического уравнения (3):

Характеристическое уравнение разомкнутой системы (3) имеет один правый корень, следовательно, разомкнутая система неустойчива.
Построим годограф Найквиста. Для этого определим частотную передаточную функцию разомкнутой системы и ее действительную и мнимую части.
 (4)
(4)
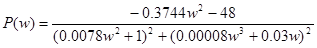 (5)
(5)
 (6)
(6)
Используя выражения (5) и (6), заполним таблицу:
Таблица 1.3.1
| w | 0 | - | - | ∞ |
| P | -48 | 0 | - | 0 |
| Q | 0 | - | 0 | 0 |
Построим годограф Найквиста (Рис. 1.3.1):
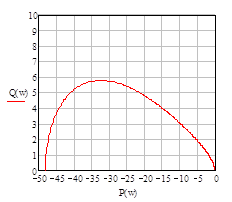
Рис. 1.3.1
Для случая, когда разомкнутая система неустойчива критерий Найквиста звучит следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста охватывал особую точку (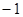 ;
; 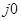 ) в положительном направлении на угол
) в положительном направлении на угол 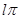 , где l – число правых корней характеристического уравнения разомкнутой системы.
, где l – число правых корней характеристического уравнения разомкнутой системы.
|
|
|
Число правых корней характеристического уравнения разомкнутой системы (3) равно единице (l = 1), полученный годограф не охватывает особую точку (-1, j0) на угол l π=π (годограф охватывает особую точку в направлении по часовой стрелке), следовательно, критерий Найквиста не выполняется и система неустойчива.
Б) Критерий Найквиста (на плоскости ЛЧХ)
Построим ЛЧХ заданной системы, для этого определим расчетные выражения для L (w) и φ(w):
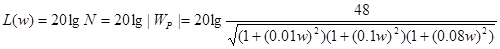 (7)
(7)
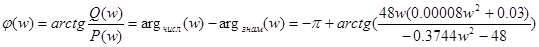 (8)
(8)
Для построения асимптотической ЛАЧХ найдем параметры:
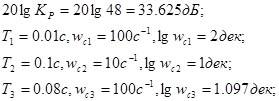
ЛФЧХ системы также можно построить как геометрическую сумму ЛФЧХ отдельных звеньев системы.
Графики расчетных ЛЧХ, построенные по формулам (7) и (8) изображены на рисунке (1.3.2):

Рис. 1.3.2
wср (частота среза) – частота, соответствующая пересечению ЛАЧХ с осью lgw;
wкр (критическая частота) – частота, соответствующая пересечению ЛФЧХ уровня –π;
Система устойчива, если выполняется условие:
wср < wкр
Данное условие не выполняется, следовательно, система неустойчива. Аналогичный вывод можно сделать по асимптотической ЛАЧХ и ЛФЧХ системы, построенной как сумма отдельных звеньев, входящих в систему, изображенной на рисунке (1.3.3):
В) Критерий Михайлова
Используя характеристическое уравнение замкнутой системы (2) введем функцию Михайлова:
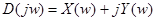 , где
, где
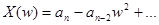 ,
,
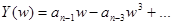 .
.
Для заданной системы функция Михайлова примет вид:
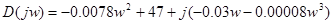
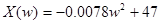 (9)
(9)
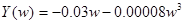 (10)
(10)
Графическое изображение функции Михайлова на комплексной плоскости при 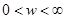 называется годографом Михайлова. Для устойчивости системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова начинался на вещественной положительной полуоси и при увеличении частоты до ∞ проходил последовательно в положительном направлении n квадрантов, нигде не обращаясь в ноль.
называется годографом Михайлова. Для устойчивости системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова начинался на вещественной положительной полуоси и при увеличении частоты до ∞ проходил последовательно в положительном направлении n квадрантов, нигде не обращаясь в ноль.
|
|
|
Используя выражения (9) и (10), заполним таблицу:
Таблица 1.3.3
| w | 0 | 77,625 | - | ∞ |
| X (w) | 47 | 0 | - | -∞ |
| Y (w) | 0 | -39,748 | 0 | -∞ |
Построим годограф Михайлова (Рис. 1.3.4):
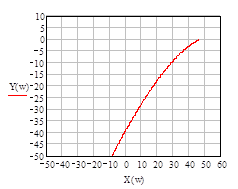
Рис. 1.3.4
Полученный годограф начинается на вещественной положительной полуоси, проходит 2 квадранта в отрицательном направлении, таким образом, критерий Михайлова не выполняется, следовательно, система неустойчива.
2. Построение области устойчивости в плоскости параметра Кр
Построим область устойчивости, используя критерий Гурвица.
Запишем характеристическое уравнение замкнутой системы в общем виде:
 .
.
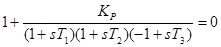
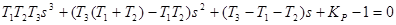
Для конкретного случая характеристическое уравнение замкнутой системы имеет вид:
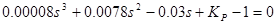 (11)
(11)
Для устойчивости системы КР должно удовлетворять необходимому условию
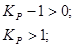

Рис. 2.1
Но заметим, что исходный КР удовлетворяет этому условию, и его изменением устойчивости замкнутой системы добиться невозможно, т. к. в ХУ ЗС (2.3) а2 <0, и зависит этот коэффициент от постоянных времени.
Построим область устойчивости в плоскости параметра Т2
Необходимое условие устойчивости:


Достаточное условие устойчивости для системы третьего порядка по критерию Гурвица имеет вид:
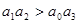
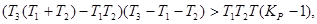
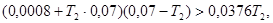
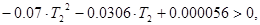
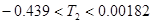
Учитывая все условия:


Рис. 2.2
Коррекция системы
Для обеспечения устойчивости системы необходимо ввести корректирующее звено с передаточной функцией вида:
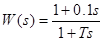
Структурная схема скорректированной системы (Рис. 3.1):
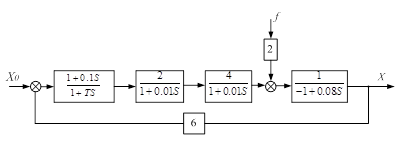
Рис. 3.1
Передаточная функция скорректированной разомкнутой системы имеет вид:
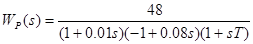 (12)
(12)
Определим параметр Т из условия обеспечения минимального запаса устойчивости (L зап =5 дБ).
Запас по амплитуде определяется на критической частоте – частоте, на которой функция φ (w) принимает значение, равное -π
Расчетное выражение для φ (w):
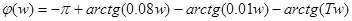
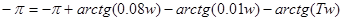 , отсюда
, отсюда
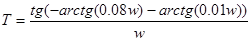 (13)
(13)
Расчетное выражение для L (w):
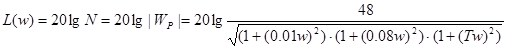 (14)
(14)
Подставим найденное выражение Т (13) в функцию L (w) (14):

На критической частоте значение функции L (w), исходя из условия обеспечения минимального запаса устойчивости, должно быть равно не менее 5 дБ.
|
|
|
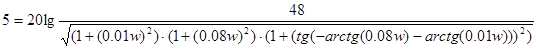
Из данного выражения найдем w кр
w кр =308,4185, следовательно,
Т=0,001198
Анализируя данное значение и область устойчивости, найденную в п. 2, можно сделать вывод, что введение корректирующего звена с передаточной функцией 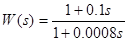 обеспечит не только устойчивость системы, но и более чем минимальный запас устойчивости по амплитуде.
обеспечит не только устойчивость системы, но и более чем минимальный запас устойчивости по амплитуде.
Построение и анализ ЛЧХ системы и годографа Найквиста скорректированной системы
Используя передаточную функцию скорректированной разомкнутой системы (12), запишем характеристическое уравнение скорректированной разомкнутой системы:
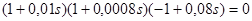 (15)
(15)
Найдем корни характеристического уравнения (15):
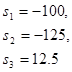
Уравнение (15) имеет один правый корень, следовательно, скорректированная разомкнутая система неустойчива.
Построим годограф Найквиста. Для этого определим частотную передаточную функцию скорректированной разомкнутой системы и ее действительную и мнимую части.
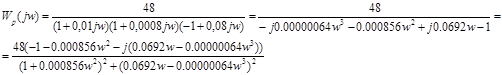
 (16)
(16)
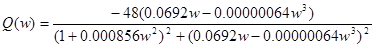 (17)
(17)
Используя выражения (16) и (17), заполним таблицу:
Таблица 4.1
| w | 0 | - | 328,8237 | ∞ |
| P | -48 | 0 | -0,485 | 0 |
| Q | 0 | - | 0 | 0 |
Построим годограф Найквиста (Рис. 4.1):
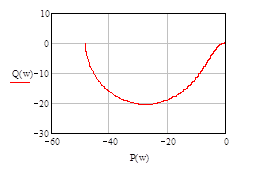

Рис. 4.1
Для случая, когда разомкнутая система неустойчива критерий Найквиста звучит следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста охватывал особую точку (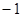 ;
; 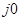 ) в положительном направлении на угол
) в положительном направлении на угол 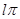 , где l – число правых корней характеристического уравнения разомкнутой системы.
, где l – число правых корней характеристического уравнения разомкнутой системы.
Число правых корней характеристического уравнения разомкнутой системы равно единице (l = 1), полученный годограф охватывает особую точку (-1, j0) на угол l π=π, следовательно, критерий Найквиста выполняется и система устойчива.
Построим ЛЧХ разомкнутой скорректированной системы:
Определим расчетные выражения для L (w) и φ(w):
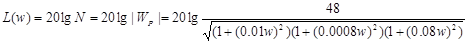 (18)
(18)
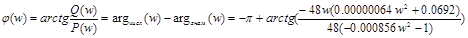 (19)
(19)
Для построения асимптотической ЛАЧХ найдем параметры:
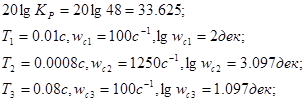
ЛФЧХ системы также можно построить как геометрическую сумму ЛФЧХ отдельных звеньев системы.
|
|
|
Графики расчетных ЛЧХ, построенные по формулам (18) и (19), изображены на рисунке (4.2):

Рис. 4.2
wср (частота среза) – частота, соответствующая пересечению ЛАЧХ с осью lgw;
wкр (критическая частота) – частота, соответствующая пересечению ЛФЧХ уровня –π;
Система устойчива, если выполняется условие:
wср < wкр
Данное условие выполняется, следовательно, система устойчива. Запас устойчивости по амплитуде: L зап = 5,8 дБ
Запас устойчивости по фазе: φзап =0,2 рад
Аналогичный вывод можно сделать по асимптотической ЛАЧХ и ЛФЧХ системы, построенной как сумма отдельных звеньев, входящих в систему.
|
|
|


