 |
Испарение с открытой поверхности в неподвижную среду.
|
|
|
|
Испарение разлитых по твердым поверхностям горючих и легковоспламеняющихся жидкостей.
Испарение с открытой поверхности в неподвижную среду.
В сосуде с открытой поверхностью (рис. 13.1) испаряющейся жидкости концентрация пара в вертикальном направлении изменяется по кривой от значения насыщенной концентрации Cs у поверхности жидкости до нуля на определенном расстоянии х от нее.
В дальнейшем принято допущение, что рассеивание паров жидкости за пределы вертикального столба над поверхностью резервуара площадью F, равной площади зеркала жидкости, отсутствует.
 |
С Cs 0
y C=0
интересующая плоскость
 |
насыщенные пары х
Нефтепродукт
y
Рис. 13.1. Координатная система определения концентрации паров испаряющейся жидкости.
Кривая изменения концентрации паров для фиксированного момента времени (t=const) имеет вид:
(13.1)
где a, b – константы;
y – координата точки, в которой определяется концентрация паров жидкости;
С(y) – концентрация пара в рассматриваемой плоскости y=const.
Константы a и b могут быть определены из граничных условий:
при y=0, в точке с нулевым значением концентрации, C(0) = 0, следовательно, b=0,
при y = x, непосредственно у поверхности жидкости после подстановки C(y) = Cs в (13.1), получим:
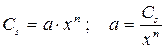
где Cs – концентрация насыщенных паров рассматриваемой жидкости.
Подставив значения констант в (13.1), получим при t=const:
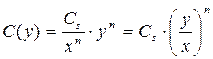, (13.2)
Средняя концентрация паров Сср (в предположении о том, что все испарение сосредоточено в вертикальном цилиндре с постоянной площадью F) будет равна:
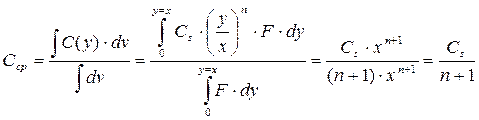(13.3)
где dv – элементарный объем области испарения.
Таким образом, при известном расстоянии х и известном значении n, можно определить как среднюю концентрацию, так и концентрацию пара нефтепродукта в любой точке по высоте над испаряющейся жидкостью. Кроме того, логичным будет предположение об изменении концентрации во времени, т.е. функцию C(y) корректнее представлять в виде C(t, y).
|
|
|
Естественно, что расстояние х изменяется для каждого продукта в зависимости от длительности испарения и температуры. Чтобы связать концентрацию паров C(y,t) с расстоянием х и временем испарения t, составим дифференциальное уравнение материального баланса, в предположении, что все пары нефтепродукта находятся в вертикальном объеме столба воздуха площадью F, равной площади испарения (сосуда) [23], [28]:
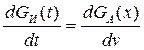(13.4)
где Gи(t) - масса жидкости, испарившейся за время t,
GА(x) - масса паров, находящихся (аккумулированных) в объеме (цилиндре) высотой х.
Массу испаряющейся со свободной поверхности жидкости можно определить на основании закона Фика с учетом поправки Стефана на конвективную диффузию [28]:
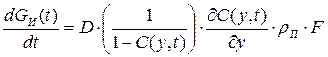(13.5)
где D - коэффициент диффузии паров нефтепродукта в воздухе с поправкой на температуру,
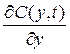- градиент концентрации паров по вертикали (частная производная по координате y),
rП - плотность паров нефтепродукта.
Значение градиента концентрации можно получить, если продифференцировать уравнение (13.2):
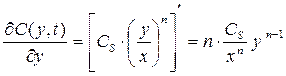(13.6)
Непосредственно на поверхности жидкости (при y = x) это уравнение принимает вид:
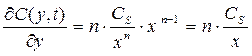(13.7)
После подстановки (13.7) в (13.5) получим:
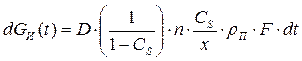(13.8)
Масса GA(х) паров жидкости, находящихся в воздухе, может быть вычислена с учетом предположения, что при изменении времени на dt будет изменяться только высота зоны распространения паров на величину dx.
Тогда, с учетом (13.3), получим:
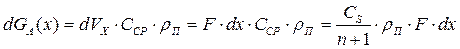(13.9)
где Vx - объем, занимаемый парами нефтепродукта.
Подставив (13.9) и (13.8) в уравнение (13.4) и проинтегрировав его в предположении, что при изменении времени от 0 до t высота зоны паров меняется от 0 до х, получим:
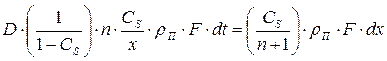(13.10)
|
|
|
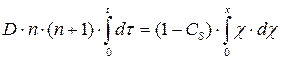(13.11)
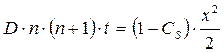(13.12)
Разрешив уравнение (13.12) относительно х, найдем расстояние от поверхности жидкости до плоскости, где концентрация паров испаряющегося нефтепродукта будет равна нулю:
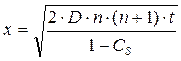(13.13)
Подставив найденное значение х в выражение (13.2), получим уравнение для определения концентрации пара в любой плоскости над поверхностью жидкости в зависимости от продолжительности испарения:
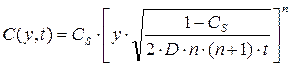(13.14)
При исследовании испаряемости нефтепродуктов установлено, что показатель степени n кривой изменения концентрации паров при испарении в условиях молекулярной диффузии колеблется около значения 2.
Тогда из уравнения (13.13):
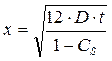(13.15)
Аналогично, из уравнения (13.14), имеем:
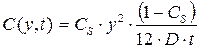(13.16)
где y - интересующее расстояние над поверхностью испаряющейся жидкости, м;
х - расстояние от поверхности нефтепродукта по вертикали до плоскости, где концентрация паров равна нулю, м;
D - коэффициент диффузии с поправкой на температуру, м2/с;
СS - концентрация насыщенных паров при данной температуре нефтепродукта, объемные доли.
Чтобы определить высоту зоны возможного воспламенения над поверхностью испаряющегося нефтепродукта х0, достаточно, задать длительность испарения и принять опасную концентрацию в виде:
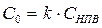(13.17)
где С0 - опасная концентрация паров, (объемные доли);
k < 1 - коэффициент безопасности, учитывающий возможные методические неточности и неточности исходных данных.
Преобразуем уравнение (13.6), зафиксировав момент времени t и обозначив временно концентрацию через С(y):
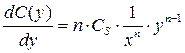
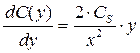
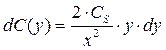
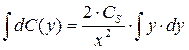
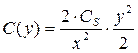
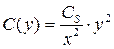
Откуда
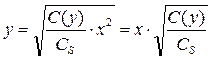
Тогда, если х0 – высота, на которой концентрация паров равна С(y), то:
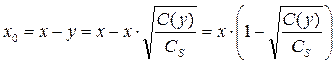
С учетом (13.6), (3.17) получим для произвольного времени t (продолжительности испарения):
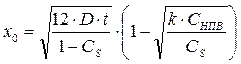(13.18)
С другой стороны, из уравнения (13.9) имеем:
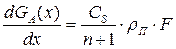
После разделения переменных и интегрирования, получим:
Массу нефтепродукта, испарившегося с площади F за время t в объем высотой х c учетом (13.4) далее будем обозначать через GИ(t):
(13.19)
где GИ(t) - масса нефтепродукта, находящегося в виде паров при нормальном давлении и температуре Т в зоне испарения высотой х;
- плотность паров нефтепродукта, вычисленная для нормального атмосферного давления при температуре Т=0°С (273.15 К);
Согласно ГОСТ Р 3.047-98 плотность паров нефтепродукта при заданной температуре (Т выраженной в °С) можно определить по формуле:
|
|
|
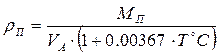
МП×10 -3 - молярная масса нефтепродукта, кг/моль;
Т°С– температура среды, °С;
VA = 22.4×10 -3 м3/моль - объем, занимаемый одним молем идеального газа при нормальном давлении и температуре 273.15 К.
Концентрация насыщенных паров определяется выражением:
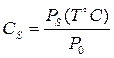
где PS(T°C) – давление насыщенных паров при температуре Т°С;
Р0 – давление в помещении или в атмосфере, выраженное в тех же единицах, что и PS(T°C).
Пример 13.1.
Определить количество ацетона, испарившегося за 1 час (t=3600 с) из открытого резервуара площадью F=1 м2, расположенного в помещении с неподвижным воздухом при температуре Т=20°С.
Установить, на какой высоте от поверхности испарения концентрация паров достигнет взрывоопасных пределов при коэффициенте безопасности k=1.
Основные параметры ацетона (С3Н6О):
молярная масса ацетона МП = 58.08 г/моль,
коэффициент диффузии D = 1.1×10 -5 м2/с,
нижний концентрационный предел воспламенения СНПВ = 2.7% (объема),
коэффициенты уравнения Антуана:
А=6.37551,
В=1281.721,
СА=237.088.
 |
Концентрация С=0
 |
y
Концентрация С=1×СНПВ
x Зона
xo взрывоопасной концентрации
Концентрация C=Cs
Ацетон
Рис. 13.2. Пояснение к примеру 13.1 определения зоны взрывоопасной концентрации.
Решение.
1. Определение давления насыщенных паров РS. Воспользуемся уравнением Антуана (12.33) и для температуры 20°С получим РS = 24.55 кПа.
2. Найдем концентрацию насыщенных паров ацетона
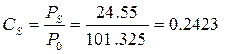
3. Значение расстояния от поверхности испарения до плоскости, где концентрация паров равна нулю (С = 0) получим по формуле (13.15):
4. Высоту зоны, в пределах которой концентрация паров ацетона будет взрывоопасной, равной произведению коэффициента безопасности на нижний концентрационный предел воспламенения (13.17), определим по формуле (13.18), учитывая, что для ацетона СНПВ =2.7%:
5. Количество испарившегося за 1 час ацетона определим по формуле (13.19):
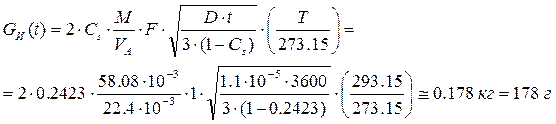
Выражение (13.16) может вызвать некоторое недоумение:
с увеличением времени t концентрация С(y, t) уменьшается. Создается ошибочное представление об уменьшении концентрации паров нефтепродукта в данной точке с течением времени.
|
|
|
Более детальный анализ (рис. 13.3) показывает, что рассматривается концентрация паров в заданной точке пространства, отсчитываемой от плоскости, где концентрация равна нулю. Тогда с течением времени (13.15) растет высота х объема, в котором распределяются пары нефтепродукта, и при y = const концентрация уменьшается.
При наличии паспортных данных конкретного нефтепродукта, значение коэффициента диффузии с поправкой на температуру вычисляют по формуле:
где Т – температура среды, К;
Т0 – температура абсолютного нуля, К;
D0 – паспортное значение коэффициента диффузии при нормальных условиях, м2/с;
n – эмпирическое значение показателя степени (n=2).
Для бензина Аи-93, например, D0 = 6.23 ×10-6 м2/с, тогда при температуре 20°С получим D20» 7.2×10-6 м2/с.
Рис. 13.3. Изменение процесса испарения во времени, связанное со смещением начала координат функции изменения концентрации паров по высоте столба паровоздушной смеси в разные моменты времени (t2 > t1).
Ориентировочное значение коэффициента диффузии D можно также получить по упрощенной формуле:
(13.20)
где М – молярная масса нефтепродукта, г/моль.
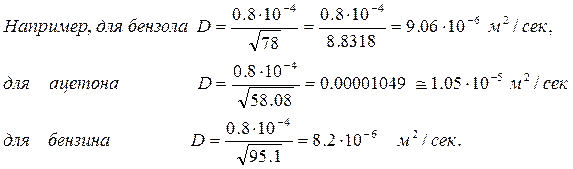
Пример 13.2.
Определить объем взрывоопасной паровоздушной смеси, которую образует 1 л автомобильного бензина при полном испарении.
Используем следующие формулы:
, 
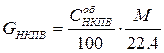где: 
– нижний концентрационный предел (по массе) воспламенения паров в воздухе, кг/м3,
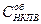- нижний концентрационный предел (по объему) воспламенения паров в воздухе, %,
М – молярная масса газа или паров, г/моль,
V – объем взрывоопасной смеси паров с воздухом, м3,
m – масса паров бензина, кг,
,
r - плотность паров, кг/м3;
Приняв 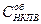=1.06% и М=95 г/моль, получим 
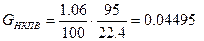кг/м3, что соответствует для 1 л бензина при плотности 750 кг/м3 (масса 1 л бензина составит 0.750 кг) объему взрывоопасной смеси паров на уровне 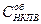=1.06 % равному 16.68 м3 (0.750 кг / 0.04495 кг/м3).
Полное испарение 1 л бензина в пустом объеме 16.68 м3 создаст концентрацию паров на уровне нижнего концентрационного предела воспламенения, т.е. опасную концентрацию.
Мольный объем равен 22.414 ×10-3 м3 /моль. Если делим молярную массу на 22.4, то получаем массовую концентрацию GНКПВ в кг/м3.
Пример 13.3.
В автомобильной цистерне объемом 6.3 м3 осталось немного бензина АИ-93 (М=95.1 г/моль). Какова должна быть масса испарившегося бензина, чтобы в цистерне образовалась взрывоопасная концентрация паровоздушной смеси (по объему)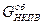 
на уровне 1.2% и на уровне 2.2%?
Используя формулу:
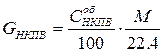, получим:
для уровня 1.2% должно испариться примерно 0.320 кг бензина (или 0.43 л при плотности бензина 750 кг/м3);
|
|
|
для уровня 2.2% должно испариться примерно 0.59 кг (или 0.785 л).
|
|
|
