1.2. Измерение

Цель измерения заключается в получении количественной информации об измеряемом объекте с гарантированной достоверностью. Как мы увидим в дальнейшем, выбор метода и средства измерений, а также методики выпол­нения эксперимента нацелен на достижение оптимального результата, причем критерием оптимальности служит, как правило, предельно достижимая точ­ность измерений при минимуме затрат на технические средства и процедуру.

) На практике широко распространен термин среднее квадратическое отклонение — (СКО). Под отклонением понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии это отклонение называется погреш­ностью измерений. Если в результаты измерений введены поправки на действие системати­ческих погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является тер­мин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность». При обработке ряда результатов измерений, свободных от систематических погрешностей, средняя квадратическая погрешность (СКП) и СКО являются одинаковой оценкой рассеяния результатов единичных измерений в ряду равноточных измерений одной и той же физической величины.

Следует заметить, что уровень точности, к которому надо стремиться, должен определяться критерием целесообразности. Известно, что увеличение точности в два раза удорожает измерение в несколько раз. В то же время уменьшение точности измерений ниже нормы приводит к браку продукции. Важно иметь в виду и значимость результата измерений. В одних случаях результат измерений имеет небольшое или локальное значение, в других он играет исключительно важную роль: от точности результата измерений может зависеть научное открытие или жизнь людей (например, при измерении кон­центрации метана в шахтах). Именно значимость результата измерений опре­деляет ту совокупность требований, которые должны предъявляться к каче­ству измерений, под которым подразумевается [11] совокупность их свойств, обусловливающих соответствие средств, метода, методики, условий измерений и состояния единства измерений требованиям измерительной задачи (техники безопасности, экологического, экономического и других факторов).

В XX веке наряду со статическими измерениями интенсивно развивались динамические измерения, а также многоканальные измерения как в статиче­ском, так и в динамическом режимах.

Измерение физической величины, принимаемой в соответствии с конкрет­ной измерительной задачей за неизменную на протяжении времени измерения, называется статическим. Теоретической метрологией разработаны хорошо известные приемы выявления и учета систематических погрешностей, а так­же обработки результатов статических измерений при наличии случайных погрешностей. Актуальными являются вопросы использования новых физи­ческих эффектов и фундаментальных констант для создания и совершенство­вания эталонов единиц в первую очередь основных величин.

Измерение изменяющейся по размеру физической величины именуется динамическим. Если измеряемую величину любой физической природы рассматривать как функцию времени, то речь идет об измерении параметров и характеристик процессов. Организация измерений в этой несомненно бо­лее сложной по сравнению со статическими измерениями ситуации является прерогативой скорее теории измерений, а перед теоретической метрологией ставится задача выбора подходящей меры и обоснования понятия точности получаемого результата. Успешным примером решения подобной метрологи­ческой задачи явилась стандартизация форм радиотехнических сигналов [12].

Однако несмотря на появление в отечественной литературе ряда моногра­фий, посвященных динамическим измерениям (например, [13]), теория дина­мических измерений требует серьезного изучения и дальнейшей разработки общих правил выполнения измерений, инвариантных к физической природе измеряемых величин, т. е. не зависящих от области измерений. Теоретической метрологии предстоит решать задачи обоснования и выбора типового набора эталонных процессов, сигналов и алгоритмов оценки точности их сравнения с экспериментальными данными.

Возникшая во второй половине XX века необходимость измерений зна­чений одной или одновременно нескольких физических величин в разных точках пространства привела к появлению многоточечных (многоканаль­ных) измерений, выполняемых информационно-измерительными системами (ИИС). Специфика ИИС и их применений потребовала разработки теоретиче­ских основ информационно-измерительной техники (ИИТ), главными процес­сами которой являются измерение, контроль, диагностика и распознавание образов [14]. Роднит эти процессы обязательный алгоритм сравнения изучаемого объекта или явления с нормируемым аналогом, т. е., в конечном счете, с так называемой «мерой», отображающей совокупность свойств на­блюдаемого предмета или эффекта. Однако здесь речь идет уже даже не о процессе, описываемом, как правило, одномерной функцией (чаще всего времени), а о физическом поле, параметры и характеристики которого отображаются многомерной функцией совокупности аргументов.

Ситуация значительно осложняется, если наблюдаемым объектом являет­ся случайное (не детерминированное) физическое поле с изменяющимися в процессе наблюдения параметрами или характеристиками. С сожалением приходится констатировать, что общая теория процессов, свойственных ИИТ, пока не разработана. Это тем более относится и к «учению о мерах», необходи­мых для количественной оценки определяемых параметров и характеристик физических полей, среди которых электромагнитное поле выделяется сво­им уникальным многообразием параметров.

1. 2. 1. Функциональная схема измерения. Таким образом, измере­ние является процессом, в котором участвует совокупность элементов, одну часть которых составляют конкретные предметы (объекты, средства изме­рений), а другую часть — понятия, определения, оговоренные процедуры, условия и т. д. Эта совокупность представлена структурной схемой, рис. 1. 2, заимствованной из [11]. Дадим толкование этим элементам, соотнося их с осо­бенностями оптической радиометрии.

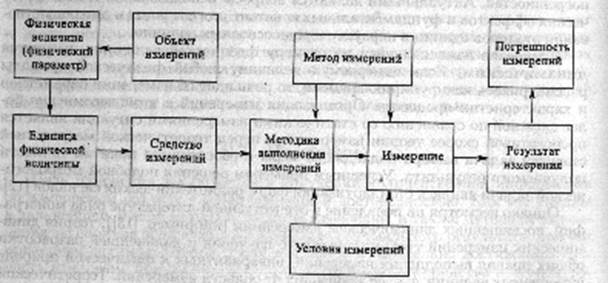
Рис. 1. 2. Основные элементы, участвующие в измерениях [11]

 

Объект измерения - это тело (физическая система, процесс, явление и т. д. ), которое характеризуется одной или несколькими измеряемыми физическими величинами.

В оптической радиометрии непосредственно объектом измерения яв­ляется оптическое излучение различных источников, распространяющееся

в разнообразных средах П° Результатам измерений судят о специфике излучателя или среды. Оптическим излучением будем считать электро­магнитные волны с длинами от ~ 1 нм до ~ 1 мм. Оптическое излучение распределено в пространстве с той или иной степенью локализации в опреде­ленном объеме, зависящей от типа и конструкции излучателя.

Очевидно, что любой объект измерения нуждается в описании его свойств. Это описание должно содержать некоторые количественные объективные признаки, информативно представляющие и отображающие объект измере­ния. Подобной цели служит физическая величина, составляющая одно из фундаментальных понятий измерения. Физическая величина есть одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в ко­личественном отношении индивидуальное для каждого из них.

Явления, величины и параметры, характеризующие оптическое излучение естественного или искусственного источника, приведены в гл. 2. Здесь же следует сделать важное замечание, касающееся весьма распространенного, но неправильно используемого термина «величина».

Нередко даже в серьезной научно-технической литературе, диссертациях, научных отчетах встречаются обороты типа «величина температуры», «вели­чина напряжения или тока» и т. д. Это неприемлемо, так как температура, напряжение, ток суть физические величины, поэтому измерению подлежат не «величина температуры», а температура, не «величина напряжения», а на­пряжение и пр.

Часто употребляется термин «размер величины», а также «значение вели­чины». Приведем их стандартизованные определения [7]. Размером вели­чины считается количественная определенность физической величины, при­сущая конкретному материальному объекту, системе, явлению или процессу. Значением величины является выражение размера физической величины в виде некоторого числа принятых для нее единиц. Как отмечал известный отечественный метролог Н. И. Тюрин, между размером и значением вели­чины есть принципиальная разница. Размер величины существует реально, независимо от того, знаем мы его или нет. Выразить размер величины мы можем при помощи любой из единиц данной величины, другими словами, при помощи числового значения. Для числового значения характерно, что при применении другой единицы оно изменяется, тогда как физический размер величины остается неизменным. Например, поставленная на чашу весов гиря имеет определенный, присущий ей неизменный размер массы, но значения массы данной гири можно выразить в миллиграммах, граммах, килограммах. Иногда возражают против широкого применения термина «размер», утвер­ждая, что он относится только к длине. Однако, по мнению Н. И. Тюрина, для столь узкого толкования никаких оснований нет.

Иными словами, результатом измерения является значение вели­чины, полученное путем ее измерения.

Наряду с величиной часто употребляются такие термины, как коэффици­ент (показатель), характеристика. Для полноты картины приведем их опре­деления [7, 11].

Параметром именуется физическая величина, рассматриваемая при определении значения измеряемой физической величины как вспомогатель­ная.

Коэффициент (или показатель) — величина, в явном или неявном виде характеризующая отношение параметров.

Характеристикой называется отличительный количественный признак (или признаки) предметов, явлений или их совокупности.

Следующим элементом в схеме рис. 1. 2 является единица физической величины, чаще просто именуемая единицей. Ею служит физическая вели­чина фиксированного размера, которой условно присвоено числовое значение, равное 1, и применяемая для количественного выражения однородных с ней физических величин.

Для обеспечения единства измерений важное значение имеет унификация единиц физических величин. В нашей стране введена Международная система единиц, на основе которой разработан ГОСТ 8. 417-81, введенный в действие с 1. 01. 1982 г. Основные достоинства Международной системы единиц [11]:

· универсальность — охват всех областей науки и техники;

· унификация единиц для всех областей и видов измерений;

· возможность воспроизведения единиц с высокой точностью в соответ­ствии с их определениями;

· единая система образования кратных и дольных единиц для единиц, имеющих собственные наименования;

· согласованность единиц — все производные единицы Международной системы единиц получают из уравнений связи между величинами, в которых коэффициенты равны 1.

Мы в дальнейшем будем использовать исключительно Международную систему единиц и дадим их определения. Вместе с тем в радиометрии уль­трафиолетового излучения, используемого в медицине, биологии, сельском хозяйстве, получили распространение некоторые редуцированные или эффек­тивные единицы.

Таким образом, характеризующая измеряемый объект физическая вели­чина должна быть воспринята каким-то техническим средством и преоб­разована им в измеряемый сигнал, отображающий в выбранных единицах входное воздействие. Эту функцию выполняет средство измерений (рис. 1. 2), определение которого приведено ранее.

С какими же видами СИ приходится иметь дело в оптической радиомет­рии? В основном в ней получили распространение меры, измерительные пре­образователи, измерительные приборы, измерительные установки и системы.

Мерой физической величины (или просто мерой) служит средство измерений, предназначенное для воспроизведения и (или) хранения физиче­ской величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.

Измерительным преобразователем (ИП) является техническое сред­ство с нормированными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измеритель­ный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи. Как будет показано в дальнейшем, большую роль в оптической радиометрии играют первичные измерительные преобразовате­ли различных принципов действия.

Первичным измерительным преобразователем (ПИП) является из­мерительный преобразователь, на который непосредственно воздействует из­меряемая физическая величина, т, е. первый преобразователь в измерительной цепи измерительного прибора (установки, системы).

Измерительный прибор - это средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне. К измерительным приборам относятся и компараторы, предназна­ченные для сравнения измеряемых величин с величинами, воспроизводимыми мерами.

Совокупность функционально объединенных мер, измерительных прибо­ров, измерительных преобразователей и других устройств, предназначенная для измерений одной или нескольких физических величин и расположенная в одном месте, называется измерительной установкой. Соответственно, измерительную установку, применяемую для поверки, именуют поверочной установкой, а входящую в состав эталона — эталонной установкой.

Измерительной системой называется совокупность функционально объединенных мер, измерительных приборов, измерительных преобразова­телей, ЭВМ и других технических средств, размещенных в разных точках контролируемого объекта с целью измерений одной или нескольких физи­ческих величин, свойственных этому объекту, и выработки измерительных сигналов в разных целях. В оптической радиометрии находят применение преимущественно измерительные информационные системы.

Наличие того или иного СИ является условием необходимым, но не только явно недостаточным, а и не первоочередным. Прежде всего следует выбрать метод измерений, затем подобрать или разработать подходящее СИ, учесть условия выполнения измерений и, наконец, продумать методику выполнения измерений. Рассмотрим методы и условия выполнения измерений.

Физическое явление или эффект, положенное в основу измерений, называ­ется принципом измерений, а прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализован­ным принципом измерений есть метод измерений.

Как и в любой области измерений, в оптической радиометрии получили распространение несколько методов измерений.

Метод измерений, при котором значение величины определяют непосред­ственно по показывающему средству измерений, именуется методом непо­средственной оценки. Быстрота процесса измерения методом непосред­ственной оценки делает его часто незаменимым для практического использо­вания, хотя точность измерения бывает обычно ограниченной.

Метод измерений, в котором измеряемую величину сравнивают с вели­чиной, воспроизводимой мерой, называется методом сравнения с мерой. Если при этом результирующий эффект воздействия измеряемой величины и меры на прибор сравнения (компаратор) доводят до нуля, то мы имеем дело с нулевым методом измерений. Если же измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отли­чающееся от значения измеряемой величины, и при этом измеряется разность двух величин, то речь идет о дифференциальном методе измерений. Этот метод позволяет получить результаты с высокой точностью даже при использовании относительно грубых средств для измерения разности. Однако реализация этого метода возможна только при условии наличия меры требу­емой точности. Это во многих случаях оказывается легче, чем изготовить СИ высокой точности для измерений методом непосредственной оценки.

Метод сравнения с мерой, в котором измеряемую величину замещают ме­рой с известным значением величины, широко известен и именуется методом измерений замещением.

Практически все применяемые в оптической радиометрии методы измере­ний являются бесконтактными, т. е. основаны на том, что чувствительный элемент средства измерений не приводится в контакт с объектом измерения.

Приходится констатировать, что в обширной научно-технической литера­туре по ИИТ практически во всех областях измерений методом часто име­нуется способ, алгоритм или методика (методика выполнения) измерений. С этим неправильным толкованием термина «метод» следует смириться, по­скольку в оптической радиометрии десятилетиями прививались такие поня­тия, как, например, методы Ньютона, Тальбота, Тэйлора, Майкельсона и др. Не отступая от традиций, мы будем использовать общепринятые термины и определения, касающиеся так называемых методов измерений в оптической радиометрии, имея в виду, что на самом деле это не метод измерений, а способ, методика или алгоритм выполнения измерений.

Условия измерений могут быть нормальными, рабочими и пре­дельными.

Нормальные условия характеризуются совокупностью значений или об­ластей значений влияющих величин, при которых изменением результата измерений пренебрегают вследствие малости. Условия измерений, при кото­рых значения влияющих величин находятся в пределах рабочих областей, именуются рабочими условиями. Предельные условия характеризуются экс­тремальными значениями измеряемой и влияющих величин, которые средство измерений может выдержать без разрушений и ухудшения его метрологиче­ских характеристик.

Обратимся к последнему элементу схемы, рис. 1. 2.

Погрешностью результата измерения (погрешностью измерения) яв­ляется характеристика результата измерения, представляющая собой откло­нение найденного значения измеряемой физической величины от ее истин­ного (действительного) значения. При этом необходимо упомянуть о часто встречающейся путанице в понятиях «точность» и «погрешность» измерения. Точность измерений — одна из характеристик качества измерения, отража­ющая близость к нулю погрешности результата измерения. Это означает, что высокая точность измерений соответствует малым погрешностям, и наоборот. Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Например, если погрешность измерений равна 10-2% = 10-4, то точность равна 104.

Поэтому расхожее выражение, например, «измерение с точностью до долей процента» неправильно, а правильно говорить о погрешности в доли процента.

1. 2. 2. Неопределенность результатов измерения. С середины 70-х годов прошлого века рядом метрологов из разных стран был поднят дискус­сионный вопрос о наличии или отсутствии истинного значения измеряемой физической величины. Утверждалось, что истинное значение всегда оста­ется неизвестным, и результат измерения следует выражать получаемым значением с оценкой не погрешности, а неопределенности результатов измерения, приемлемой для решаемой измерительной задачи.

Краткая историческая справка [15]. В 1978 г., признавая отсутствие международного единства по вопросу выражения неопределенности резуль­татов измерения, наиболее авторитетный мировой орган в метрологии — Международный комитет мер и весов (МКМВ) обратился к Международному бюро мер и весов (МБМВ) с просьбой рассмотреть эту проблему совместно с национальными метрологическими лабораториями и разработать рекомен­дацию [15].

МБМВ подготовило подробную анкету, включающую все интересующие вопросы, и разослало ее 32 национальным метрологическим лабораториям, которые, как известно, интересуются данным вопросом (и, с информативной целью, пяти международным организациям). К началу 1979 г. были получены ответы из 21 лаборатории. Почти все полагали, что важно прийти к принятой в международном масштабе методике для выражения неопределенности изме­рений и для суммирования частных составляющих неопределенности в одну общую неопределенность. Однако не было принято единого решения о методе, которым следует пользоваться. Тогда МБМВ организовало встречу с целью принятия единой и общепризнанной методики для выражения неопределен­ности; ее посетили эксперты из 11 национальных метрологических лаборато­рий. Рабочая группа по составлению отчета о неопределенностях разработала Рекомендацию INC-1 (1980) «Выражение экспериментальных неопределен­ностей». Рекомендация была принята МКМВ в 1981 г. и вновь утверждена в 1986 г. [15].

Задачу разработки подробного Руководства, основанного на Рекоменда­ции Рабочей группы (которая является скорее кратким описанием, а не по­дробным предписанием), МКМВ передана Международной организации по стандартизации (ИСО), которая могла лучше выразить потребности, возни­кающие из широких интересов промышленности и торговли.

Ответственность была возложена на Техническую консультативную груп­пу по метрологии ИСО (TAG 4), поскольку одной из ее задач является ко­ординация развития основных направлений в области измерений, которые представляют взаимный интерес для ИСО и шести организаций, принимаю­щих участие вместе с ИСО в работе TAG 4: Международной электротехниче­ской комиссии (МЭК), партнера ИСО по всемирной стандартизации; МКМВ и Международной организации законодательной метрологии (МОЗМ) — двух мировых метрологических организаций; Международного союза по чистой и прикладной химии (ИЮПАК) и Международного союза по чистой и при­кладной физике (ИЮПАП), двух международных союзов, представляющих химию и физику, и Международной федерации клинической химии (МФКХ).

TAG 4, в свою очередь, учредила Рабочую группу 3 (ISO/TAG 4/WG 3), состоящую из экспертов, предложенных МБМВ, МЭК, ИСО и МОЗМ и назна­ченных председателем TAG 4.

 

Перед ней была поставлена следующая задача: разработать руководящий документ, базирующийся на Рекомендации Рабочей группы МБМВ по составлению отчета о неопределенностях, кото­рый давал бы правила выражения неопределенности результатов измерения и использовался бы службами стандартизации, калибровки, аккредитации лабораторий и метрологии.

 

Цель данного руководства:

· обеспечить полную информацию о том, как составлять отчеты о неопре­деленностях;

· предоставить основу для международного сличения результатов изме­рения.

Результатом многолетней деятельности столь представительных между­народных метрологических организаций явилось Руководство по выражению неопределенности результатов измерения [15].

В нем неопределенностью результатов измерения рекомендовано считать параметр, связанный с результатом измерений и характе­ризующий рассеяние значений, которые достаточно обоснованно могли бы быть приписаны измеряемой величине.

Параметром может быть, например, стандартное отклонение (или число, кратное ему), или половина интервала, имеющего указанный уровень дове­рия 1).

Неопределенность результатов измерения состоит, в общем случае, из мно­гих составляющих. Некоторые из этих составляющих могут быть оценены на основании статистического распределения результатов рядов измерений и могут характеризоваться экспериментальными стандартными отклонени­ями. Другие составляющие, которые также могут характеризоваться стан­дартными отклонениями, вычисляются из предполагаемого распределения вероятностей, основанного на опыте или другой информации.

Подразумевается, что результат измерения является лучшей оценкой зна­чения измеряемой величины, и что все составляющие неопределенности, включая составляющие, обусловленные систематическими эффектами, на­пример, связанные с поправками и эталонами, приводят к рассеянию.

На практике существует много возможных источников неопределенности при измерении, в том числе:

a) неполное определение измеряемой величины;

b) несовершенная реализация определения измеряемой величины;

c) нерепрезентативная выборка — измеренный образец может не представ­лять определяемую измеряемую величину;

d) неадекватное знание зависимости эффектов от условий окружающей среды, влияющих на измерение, или несовершенное измерение условий окру­жающей среды;

e) субъективная систематическая погрешность оператора при снятии по­казаний аналоговых приборов;

f) конечная разрешающая способность прибора или порог чувствительно­сти;

g) неточные значения, приписанные эталонам, используемым для измере­ния, и стандартным образцам веществ и материалов;

h) неточные значения констант и других параметров, полученных из внеш­них источников и используемых в алгоритме обработки данных;

i) аппроксимации и предположения, используемые в методе изменения и измерительной процедуре;

j) измерения в повторных наблюдениях измеряемой величины при явно одинаковых условиях.

1) При оценке неопределенности измерения мерой рассеяния наблюдений рекомендовано [15] считать не среднее квадратическое, а стандартное отклонение, являющееся по существу синонимом СКО.

Эти источники не обязательно являются независимыми, и некоторые из источников от а до i могут вносить вклад в источник j. Конечно, неизвест­ный систематический эффект не может быть учтен в оценке неопределенности результата измерения, но он вносит вклад в его погрешность.

При оценке точности эталонов, участвующих в международных сличе­ниях, российские метрологи вынуждены представлять результаты воспроиз­ведения единиц с оценкой не погрешности, а неопределенности результатов измерений в соответствии с Руководством [15].

Поэтому приведем здесь некоторые основные сведения о типах неопреде­ленности, которые нам необходимы, когда в дальнейшем будут представлены конкретные примеры оценки неопределенности при определении результатов нескольких фотометрических экспериментов.

Начнем с терминов в контексте [15], а конкретизация их применительно к фотометрическим задачам заимствована нами из работ [4а, 16].

Стандартная неопределенность — неопределенность результата изме­рения, выраженная как стандартное отклонение.

Оценка (неопределенности) по типу А — метод оценивания неопре­деленности путем статистического анализа рядов наблюдений.

Оценка (неопределенности) по типу В — метод оценивания неопре­деленности иным способом, чем статистический анализ рядов наблюдений.

Суммарная стандартная неопределенность — стандартная неопре­деленность результата измерения, когда результат получают из значений ряда других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других вели­чин, взвешенными в соответствии с тем, как результат измерения изменяется в зависимости от изменения этих величин.

Расширенная неопределенность — величина, определяющая интер­вал вокруг результата измерения, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли быть приписаны измеряемой величине.

Примечания.

1. Эта часть распределения может рассматриваться как вероятность охва­та или уровень доверия для интервала.

2. Установление связи между конкретным уровнем доверия и интервалом, определенным расширенной неопределенностью, требует явных и неявных предположений относительно распределения вероятностей, характеризуемого результатом измерения и его суммарной стандартной неопределенностью. Уровень доверия, который может быть приписан этому интервалу, может быть известен только до той степени, в которой такие предположения могут быть оправданы.

Коэффициент охвата k— числовой коэффициент, используемый как множитель суммарной стандартной неопределенности для получения расши­ренной неопределенности, обычно находящийся в диапазоне от 2 до 3.

Приступим к описанию алгоритмов оценки неопределенности. Поскольку речь идет об эталонных измерениях, как правило, выполняемых на установ­ках в ранге первичных и вторичных эталонов, имеются в виду повторные измерения.

В первую очередь при проведении подобных измерений оценивается стан­дартная неопределенность.

3. Основы оптической радиометрии

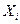Оценка стандартной неопределенности по результатам повтор­ных измерений. Значение:  физической величины  может быть опреде­лено из показаний  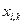повторных независимых измерений при условии, что 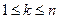. Среднее  является оценкой значения величины, а стандартное отклонение среднего 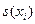 представляет собой квадратный корень эмпириче­ской дисперсии. Они рассчитываются статистическими методами:

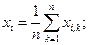
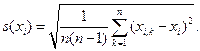                  (1. 1)

Если количество показаний достаточно велико (на практике ), то стандартное отклонение среднего считается стандартной неопределенностью 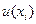, соответствующей значениям величины 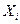 . Если стандартное откло­нение  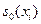измерений такого типа известно по результатам  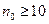преды­дущих измерений и среднее значение рассчитано по показаниям , то

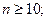
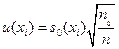для   для 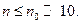     (1. 2)

Этот метод «приписывания» значения и неопределенности некоторой ве­личине, основанный на отдельных показаниях, называют «оценкой стандарт­ной неопределенности типа А». Число степеней свободы 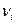, эффективное с точ­ки зрения описания характера неопределенности, определяется выражением

 .

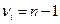Коэффициент корреляции для одновременных повторных изме­рений. Значения 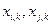 для двух величин 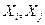могут оказаться кор­релированными. Это означает, что существует неизвестная третья величина, которая оказывает влияние на значения двух других упомянутых величин. Корреляция между этими двумя значениями может иметь место, если они получены одновременно или, говоря более точно, если они найдены в период времени, который короче по сравнению с постоянной времени изменения тре­тьей величины.

Эмпирическая ковариантность 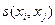 характеризует степень корреля­ции двух средних значений и является положительной, хотя возможны и от­рицательные ее значения. Исходя из ковариантности  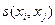и двух соот­ветствующих дисперсий 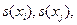можно рассчитать коэффициент корре­ляции  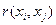двух средних значений; при этом возможные значения будут ограничены интервалом :

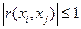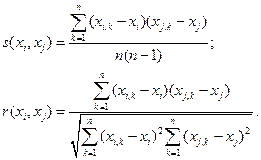                                        (1. 3)

Составляющая неопределенности 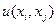 с учетом корреляции двух величин рассчитывается как произведение их стандартных неопределенностей и коэффициента корреляции:

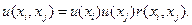                                           (1. 4)

Примечание. Корреляция двух величин возникает в результате влия­ния третьей величины, специфически воздействующей на две другие. В случае если коэффициент корреляции положителен, отношение этих двух величин сильно снижает это влияние, в то время как при отрицательном коэффициенте корреляции их произведение практически устраняет влияние третьей величи­ны.

Другие способы оценки стандартной неопределенности. Обычно выход­ная величина образуется в результате суммарного воздействия нескольких входных величин, но часто многие из них оказывают незначительное влияние назначение выходной величины. Поэтому нет необходимости в проведении но­вых измерений этих входных величин. Из результатов предыдущих измерений может быть известно, что значения этой величины симметрично распределены в интервале, ограниченном пределами 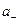, 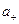. Тогда для среднего значения  и полуширины а получим, что

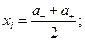
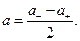                                                (1. 5)

Равномерное прямоугольное распределение вероятностей в пределах ин­тервала — это самый распространенный случай (если нет никакой другой ин­формации). Тогда соответствующая стандартная неопределенность для этой величины равна

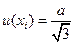                                                         (1. 6)

Если изменение значения некоторой величины в пределах интервала полу­ширины а подчиняется синусоидальному закону с периодом, много меньшим продолжительности измерения, то соответствующая стандартная неопреде­ленность для этой величины определяется из уравнения (синусоидальный вариант)

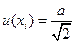                                                         (1. 7)

В случае если значение величины изменяется в пределах интервала по­лушириной а в соответствии с треугольным распределением с максимумом в центре, тогда соответствующая стандартная неопределенность для этой величины рассчитывается следующим образом (треугольный вариант):

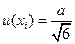                                                         (1. 8)

Пусть значения 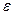 некоторой величины малы  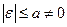и изменяются по закону прямоугольного распределения вероятностей в интервале с полу­шириной а, причем упомянутая величина является аргументом функции, симметричной относительно центра интервала (например, косинусоидальная Функция, 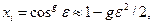проекция некоторой области). Тогда значения  и стандартная неопределенность 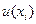 определяются в соответствии с выражениями

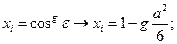
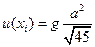                                   (1. 9)

В некоторых случаях в уравнении (1. 9) удобнее приравнять  единице и включить поправку в суммарную стандартную неопределенность:

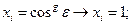
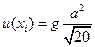                                  (1. 10)

Этот метод «приписывания» значения и неопределенности некоторой ве­личине, основанный на определенной форме распределения, называют «оцен­кой стандартного отклонения типа В». С учетом

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: