 |
Примеры применения закона Паскаля.
|
|
|
|
1. Гидравлический пресс (рис. 5.1.5).
Рис. 5.1.5. Рис. 5.1.6. Рис. 5.1.7.
Если к правому колену гидравлического пресса приложить силу F1, то из закона Паскаля: p1 = p2, следует
, Þ 
, т.к. S2 > S1.
С помощью такого пресса, прикладывая к правому поршню силу F1, с левой стороны получим большую силу F2. При этом, если правый поршень сместится на L1, то из условия несжимаемости жидкости: 
, получим, что левый стержень поднялся на 
.
Свойство гидравлического пресса: сколько выигрываем в силе, столько проигрываем в расстоянии.
2. Сообщающиеся сосуды.
а) Однородная жидкость в сообщающихся сосудах устанавливается на одном горизонтальном уровне (рис. 5.1.6).
б) Для различных жидкостей (рис. 5.1.7):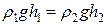 
, Þ 
.
3. Гидростатический парадокс. (рис. 5.1.8).
Рис. 5.1.8.
Возьмем три сосуда различной формы, но с одинаковой площадью сечения дна. Предположим эта площадь равна S = 20 см2 = 0,002 м2. Уровень воды во всех сосудах одинаков и равен h = 0,1 м. Однако из-за различной формы сосудов в них находится разное количество воды. В частности, в сосуде A налита вода весом 3 Н, в сосуде B – весом 2 Н и в сосуде C – весом 1 Н.
Гидростатическое давление на дно во всех сосудах равно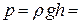 
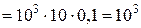Па. Одинакова и сила давления воды на дно сосудов 
Н. Как может вода весом 1 Н в третьем сосуде создать силу давления 2 Н?
Для объяснения гидростатического парадокса следует учесть силы реакции, действующие со стороны стенок (рис. 5.1.9).
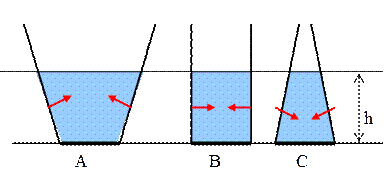
Рис. 5.1.9.
Закон Архимеда.
Архимед (287 – 212 г. до н.э.) рассмотрел задачу о телах, погруженных в жидкость. Он установил, что вес тела, погруженного в жидкость, уменьшается, что связано с действием на тело выталкивающей силы или силы Архимеда. Эта сила возникает из-за того, что давление жидкости увеличивается с глубиной, поэтому сила, действующая на тело сверху вниз, меньше силы давления, направленной снизу вверх.
|
|
|
Закон Архимеда. На тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) выталкивающая сила, численно равная весу вытесненной телом жидкости (газа), в объеме погруженной части тела, линия действия которой направлена в сторону, противоположную весу вытесненной жидкости и проходит через центр тяжести вытесненной жидкости (газа).
Доказательство закона Архимеда.
Рис. 5.2.1. Рис. 5.2.2. Рис. 5.2.3.
1. Рассмотрим, для простоты, тело в форме прямоугольного параллепипеда или цилиндра, погруженного в жидкость плотности r (рис. 5.2.1). Найдем результирующую поверхностных сил давления, действующих на тело. Силы, действующие на боковую поверхность тела, стремятся сжать его, они взаимно уравновешены. Тогда выталкивающая сила равна 
,
где 
и 
. Откуда получим
, Þ 
. (5.2.1)
Замечание. Если тело погружено в жидкость не полностью, а частично, под объемом V в формуле (5.2.1), следует понимать объем погруженной части тела.
2. Докажем закон Архимеда в общем случае тела произвольной формы (рис. 5.2.2). Для этого используем принцип отвердевания.
На тело, погруженное в жидкость (рис. 5.2.2), действуют поверхностные силы давления, результирующая которых равна выталкивающей силе:
.
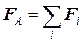Мысленно удалим тело и заполним образовавшуюся полость жидкостью (рис. 5.2.3). Очевидно, что при этом равновесие жидкости в сосуде не нарушается. Жидкость, которая заняла место удаленного тела, можно считать отвердевшей. На эту жидкость действует сила тяжести 
, приложенная к ее центру тяжести. Кроме того, на нее действуют со стороны окружающей жидкости те же поверхностные силы давления 
, которые действовали на тело. Как и вся жидкость, этот отвердевший объем находится в равновесии, т.е.
.Þ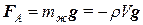 
.
Для того, чтобы была равна нулю и сумма моментов внешних сил относительно оси, проходящей через центр тяжести отвердевшего объема, результирующая сил давления должна проходить через центр тяжести.
|
|
|
Тем самым доказаны все утверждения закона Архимеда.
|
|
|
