Пружинный и математический маятники, колебания

1. Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии го­ри­зон­таль­но­го пру­жин­но­го ма­ят­ни­ка 1 с. Каким будет пе­ри­од ее ко­ле­ба­ний, если массу груза ма­ят­ни­ка уве­ли­чить в 2 раза, а жест­кость пру­жи­ны вдвое умень­шить? (Ответ дайте в се­кун­дах.)

За­да­ние 4 № 526

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка про­пор­ци­о­на­лен пе­ри­о­ду ко­ле­ба­ний груза, ко­то­рый опре­де­ля­ет­ся вы­ра­же­ни­ем

.

Сле­до­ва­тель­но, уве­ли­че­ние массы груза ма­ят­ни­ка в 2 раза и умень­ше­ние жест­ко­сти пру­жи­ны в 2 раза при­ве­дет к уве­ли­че­нию пе­ри­о­да ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка в 2 раза: Он ока­жет­ся рав­ным .

Ответ: 2

2. Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка 1 с. Каким будет пе­ри­од ее ко­ле­ба­ний, если массу груза ма­ят­ни­ка и жест­кость пру­жи­ны уве­ли­чить в 4 раза? (Ответ дайте в се­кун­дах.)

За­да­ние 4 № 601

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка в два раза мень­ше пе­ри­о­да ко­ле­ба­ний са­мо­го ма­ят­ни­ка. В свою оче­редь, пе­ри­од ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка за­ви­сит толь­ко от от­но­ше­ния массы груза и жест­ко­сти пру­жи­ны:

.

Таким об­ра­зом, од­но­вре­мен­ное их уве­ли­че­ние в 4 раза не при­ве­дет к из­ме­не­нию пе­ри­о­да ко­ле­ба­ний по­тен­ци­аль­ной энер­гии.

Ответ: 1

3. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти по­тен­ци­аль­ной энер­гии ма­те­ма­ти­че­ско­го ма­ят­ни­ка (от­но­си­тель­но по­ло­же­ния его рав­но­ве­сия) от вре­ме­ни.

Ка­ко­ва пол­ная ме­ха­ни­че­ская энер­гия ма­ят­ни­ка в мо­мент вре­ме­ни, со­от­вет­ству­ю­щий на гра­фи­ке точке D? (Ответ дайте в джо­у­лях.)

За­да­ние 4 № 605

Ре­ше­ние.

При ко­ле­ба­нии ма­те­ма­ти­че­ско­го ма­ят­ни­ка вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской энер­гии, так как на ма­ят­ник не дей­ству­ет ни­ка­ких внеш­них сил, со­вер­ша­ю­щих ра­бо­ту. В любой мо­мент вре­ме­ни имеем

.

Из гра­фи­ка видно, что в мо­мен­ты вре­ме­ни 0 с и 2 с по­тен­ци­аль­ная энер­гия имеет мак­си­мум, а зна­чит, в эти мо­мен­ты вре­ме­ни ее зна­че­ние сов­па­да­ет с ве­ли­чи­ной пол­ной ме­ха­ни­че­ской энер­гии. От­сю­да

.

Ответ: 16

4. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти по­тен­ци­аль­ной энер­гии ма­те­ма­ти­че­ско­го ма­ят­ни­ка (от­но­си­тель­но по­ло­же­ния его рав­но­ве­сия) от вре­ме­ни.

Ка­ко­ва ки­не­ти­че­ская энер­гия ма­ят­ни­ка в мо­мент вре­ме­ни ? (Ответ дайте в джо­у­лях.)

За­да­ние 4 № 606

Ре­ше­ние.

При ко­ле­ба­нии ма­те­ма­ти­че­ско­го ма­ят­ни­ка вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской энер­гии, так как на ма­ят­ник не дей­ству­ет ни­ка­ких внеш­них сил, со­вер­ша­ю­щих ра­бо­ту. В любой мо­мент вре­ме­ни имеем

.

Из гра­фи­ка видно, что в мо­мент вре­ме­ни по­тен­ци­аль­ная энер­гия об­ра­ща­ет­ся в ноль. Сле­до­ва­тель­но, в этот мо­мент вре­ме­ни ки­не­ти­че­ская энер­гия сов­па­да­ет с пол­ной ме­ха­ни­че­ской энер­ги­ей. Зна­че­ние по­след­ней можно найти из гра­фи­ка в точ­ках мак­си­му­ма по­тен­ци­аль­ной энер­гии (когда об­ра­ща­ет­ся в ноль ки­не­ти­че­ская энер­гия). В итоге, имеем

.

Ответ: 20

5. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти по­тен­ци­аль­ной энер­гии ма­те­ма­ти­че­ско­го ма­ят­ни­ка (от­но­си­тель­но по­ло­же­ния его рав­но­ве­сия) от вре­ме­ни.

Ка­ко­ва ки­не­ти­че­ская энер­гия ма­ят­ни­ка в мо­мент вре­ме­ни ? (Ответ дайте в джо­у­лях.)

За­да­ние 4 № 607

Ре­ше­ние.

При ко­ле­ба­нии ма­те­ма­ти­че­ско­го ма­ят­ни­ка вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской энер­гии, так как на ма­ят­ник не дей­ству­ет ни­ка­ких внеш­них сил, со­вер­ша­ю­щих ра­бо­ту. В любой мо­мент вре­ме­ни имеем

.

Из гра­фи­ка видно, что в мо­мент вре­ме­ни 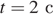по­тен­ци­аль­ная энер­гия до­сти­га­ет мак­си­му­ма и сов­па­да­ет со зна­че­ни­ем пол­ной ме­ха­ни­че­ской энер­гии. Сле­до­ва­тель­но, в этот мо­мент вре­ме­ни ки­не­ти­че­ская энер­гия об­ра­ща­ет­ся в ноль. В итоге, имеем

.

Ответ: 0

6. На ри­сун­ке дан гра­фик за­ви­си­мо­сти ко­ор­ди­на­ты ма­те­ри­аль­ной точки от вре­ме­ни.

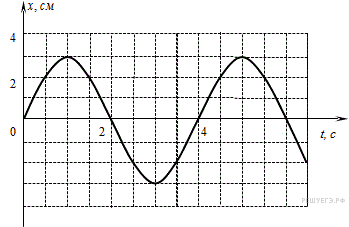
Ка­ко­ва ча­сто­та ко­ле­ба­ний? (Ответ дайте в гер­цах.)

За­да­ние 4 № 609

Ре­ше­ние.

Из гра­фи­ка видно, что пе­ри­од ко­ле­ба­ния тела со­став­ля­ет 4 се­кун­ды. От­сю­да на­хо­дим ча­сто­ту

.

Ответ: 0,25

0,25

7. Ско­рость тела, со­вер­ша­ю­ще­го гар­мо­ни­че­ские ко­ле­ба­ния ме­ня­ет­ся с те­че­ни­ем вре­ме­ни в со­от­вет­ствии с урав­не­ние , где все ве­ли­чи­ны вы­ра­же­ны в СИ. Ка­ко­ва ам­пли­ту­да ко­ле­ба­ний ско­ро­сти? (Ответ дайте в мет­рах в се­кун­ду.)

За­да­ние 4 № 631

Ре­ше­ние.

Общий вид за­ко­на из­ме­не­ния ско­ро­сти тела со вре­ме­нем, со­вер­ша­ю­ще­го ко­ле­ба­ния, имеет вид

,

где — ам­пли­ту­да ко­ле­ба­ний ско­ро­сти. Срав­ни­вая с за­клю­ча­ем, что ам­пли­ту­да ко­ле­ба­ний ско­ро­сти равна .

Ответ: 0,03

0,03

8. Ко­ле­ба­тель­ное дви­же­ние тела за­да­но урав­не­ни­ем:

 

 

где Чему равна ам­пли­ту­да ко­ле­ба­ний? (Ответ дайте в сан­ти­мет­рах.)

За­да­ние 4 № 635

Ре­ше­ние.

Общий вид за­ко­на из­ме­не­ния со вре­ме­нем ко­ор­ди­на­ты тела, со­вер­ша­ю­ще­го ко­ле­ба­ния, имеет вид

 

 

где — ам­пли­ту­да ко­ле­ба­ний.

Срав­ни­вая с за­клю­ча­ем, что ам­пли­ту­да ко­ле­ба­ний равна

Ответ: 5

9. Груз, под­ве­шен­ный на пру­жи­не жёстко­стью со­вер­ша­ет сво­бод­ные гар­мо­ни­че­ские ко­ле­ба­ния. Какой долж­на быть жёсткость пру­жи­ны, чтобы ча­сто­та ко­ле­ба­ний этого груза уве­ли­чи­лась в 2 раза? (Ответ дайте в Н/м.)

За­да­ние 4 № 636

Ре­ше­ние.

Ча­сто­та ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка свя­за­на с жёстко­стью пру­жи­ны и мас­сой груза со­от­но­ше­ни­ем

 

 

Сле­до­ва­тель­но, при не­из­мен­ной массе груза для уве­ли­че­ния ча­сто­ты ко­ле­ба­ний в два раза, не­об­хо­ди­мо уве­ли­чить жёсткость пру­жи­ны в 4 раза. Таким об­ра­зом, жёсткость пру­жи­ны долж­на быть равна

 

 

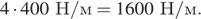
Ответ: 1600 Н/м

Ответ: 1600

10. На ри­сун­ке изоб­ра­же­на за­ви­си­мость ам­пли­ту­ды уста­но­вив­ших­ся ко­ле­ба­ний ма­ят­ни­ка от ча­сто­ты вы­нуж­да­ю­щей силы (ре­зо­нанс­ная кри­вая).

 

 

 

Ка­ко­ва ам­пли­ту­да ко­ле­ба­ний этого ма­ят­ни­ка при ре­зо­нан­се? (Ответ дайте в сан­ти­мет­рах.)

За­да­ние 4 № 637

Ре­ше­ние.

Ре­зо­нан­сом на­зы­ва­ет­ся яв­ле­ние рез­ко­го воз­рас­та­ния ам­пли­ту­ды вы­нуж­ден­ных ко­ле­ба­ний при при­бли­же­нии ча­сто­ты вы­нуж­да­ю­щей силы к соб­ствен­ной ча­сто­те ма­ят­ни­ка. Из гра­фи­ка видно, что ре­зо­нанс про­ис­хо­дит при зна­че­нии ча­сто­ты вы­нуж­да­ю­щей силы в 2 Гц, ам­пли­ту­да ко­ле­ба­ний ма­ят­ни­ка при этом равна 10 см.

Ответ: 10

11. На гра­фи­ках пред­став­ле­на за­ви­си­мость ко­ор­ди­на­ты х цен­тров масс тела а и тела б от вре­ме­ни t при гар­мо­ни­че­ских ко­ле­ба­ни­ях вдоль оси Ox.

 

 

На каком рас­сто­я­нии друг от друга на­хо­дят­ся цен­тры масс тел а и б в мо­мент вре­ме­ни 0 с? (Ответ дайте в сан­ти­мет­рах.)

За­да­ние 4 № 713

Ре­ше­ние.

Из пред­став­лен­ных гра­фи­ков видно, что в мо­мент вре­ме­ни 0 с тело а на­хо­ди­лось в по­ло­же­нии рав­но­ве­сия а тело б от­кло­ни­лось на мак­си­маль­ное рас­сто­я­ние: Таким об­ра­зом, в мо­мент вре­ме­ни 0 с цен­тры масс тел а и б от­сто­я­ли друг от друга на рас­сто­я­нии

Ответ: 2

12. На ри­сун­ке пред­став­ле­ны гра­фи­ки за­ви­си­мо­сти ко­ор­ди­на­ты х цен­тров масс тела а и тела б от вре­ме­ни t при гар­мо­ни­че­ских ко­ле­ба­ни­ях вдоль оси Ox.

 

 

На каком рас­сто­я­нии друг от друга на­хо­дят­ся цен­тры масс тел а и б в мо­мент вре­ме­ни ? (Ответ дайте в сан­ти­мет­рах.)

За­да­ние 4 № 714

Ре­ше­ние.

Из пред­став­лен­ных гра­фи­ков видно, что в мо­мент вре­ме­ни тело a от­кло­ни­лось на мак­си­маль­ное рас­сто­я­ние , а тело б на­хо­ди­лось в по­ло­же­нии рав­но­ве­сия: . Таким об­ра­зом, в мо­мент вре­ме­ни цен­тры масс тел а и б от­сто­я­ли друг от друга на рас­сто­я­нии

.

Ответ: 2

13. На ри­сун­ке пред­став­ле­ны гра­фи­ки за­ви­си­мо­сти ко­ор­ди­на­ты х цен­тров масс тела а и тела б от вре­ме­ни t при гар­мо­ни­че­ских ко­ле­ба­ни­ях вдоль оси Ox.

 

 

В какой мо­мент вре­ме­ни тело б дви­жет­ся с такой же ско­ро­стью, с какой тело а дви­га­лось в мо­мент вре­ме­ни 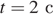? (Ответ дайте в се­кун­дах.)

За­да­ние 4 № 715

Ре­ше­ние.

В мо­мент вре­ме­ни 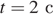тело а про­хо­дит по­ло­же­ние рав­но­ве­сия, дви­га­ясь про­тив оси Ox. По­сколь­ку пе­ри­о­ды и ам­пли­ту­ды ко­ле­ба­ний тел а и б сов­па­да­ют, тело б имеет такую же ско­рость, что и тело а в мо­мент вре­ме­ни 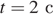, когда оно также про­хо­дит по­ло­же­ние рав­но­ве­сия в на­прав­ле­нии про­тив оси Ox. Из гра­фи­ка видно, что это со­от­вет­ству­ет мо­мен­ту вре­ме­ни .

Ответ: 1

14. Гиря мас­сой 4 кг, под­ве­шен­ная на сталь­ной пру­жи­не, со­вер­ша­ет сво­бод­ные ко­ле­ба­ния с пе­ри­о­дом 2 с. С каким пе­ри­о­дом будет со­вер­шать сво­бод­ные ко­ле­ба­ния гиря мас­сой 1 кг, под­ве­шен­ная на этой пру­жи­не? (Ответ дайте в се­кун­дах.)

За­да­ние 4 № 717

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка свя­зан с мас­сой груза и жест­ко­стью пру­жи­ны со­от­но­ше­ни­ем

.

Сле­до­ва­тель­но, если оста­вить пру­жи­ну преж­ней, а массу груза умень­шить в 4 раза, пе­ри­од умень­шит­ся в 2 раза и будет равен 1 с.

Ответ: 1

15. При сво­бод­ных ко­ле­ба­ни­ях груза на нити как ма­ят­ни­ка его ки­не­ти­че­ская энер­гия из­ме­ня­ет­ся от 0 Дж до 50 Дж, мак­си­маль­ное зна­че­ние по­тен­ци­аль­ной энер­гии 50 Дж. Чему равна пол­ная ме­ха­ни­че­ская энер­гия груза при таких ко­ле­ба­ния? (Ответ вы­ра­зи­те в джо­у­лях.)

За­да­ние 4 № 719

Ре­ше­ние.

При сво­бод­ных ко­ле­ба­ни­ях груза на нити вы­пол­ня­ет­ся закон со­хра­не­ния пол­ной ме­ха­ни­че­ской энер­гии:

 

 

Ми­ни­му­му ки­не­ти­че­ской энер­гии со­от­вет­ству­ет мак­си­мум по­тен­ци­аль­ной, и на­о­бо­рот. Таким об­ра­зом, пол­ная ме­ха­ни­че­ская энер­гия груза во время ко­ле­ба­ний равна

 

Ответ: 50 Дж

Ответ: 50

16. В таб­ли­це пред­став­ле­ны дан­ные о по­ло­же­нии ша­ри­ка, гар­мо­ни­че­ски ко­леб­лю­ще­го­ся вдоль оси Ox в раз­лич­ные мо­мен­ты вре­ме­ни.

 

t, с	0,0	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8	2,0	2,2	2,4	2,6	2,8	3,0	3,2
х, мм												–2	–5	–10	–13	–15	–13

 

Ка­ко­ва ам­пли­ту­да ко­ле­ба­ний ша­ри­ка? (Ответ дайте в мил­ли­мет­рах.)

За­да­ние 4 № 3788

Ре­ше­ние.

Ко­ле­ба­ния сим­мет­рич­ны от­но­си­тель­но по­ло­же­ния рав­но­ве­сия. Ам­пли­ту­дой на­зы­ва­ет­ся ве­ли­чи­на мак­си­маль­но­го от­кло­не­ния из по­ло­же­ния рав­но­ве­сия. Из при­ве­ден­ной таб­ли­цы видно, что ко­ле­ба­ния сим­мет­рич­ны от­но­си­тель­но точки , а мак­си­маль­ное от­кло­не­ние до­сти­га­ет­ся впер­вые через 1,0 с и со­став­ля­ет 15 мм, имен­но та­ко­ва ве­ли­чи­на ам­пли­ту­ды дан­но­го ко­ле­ба­ния.

Ответ: 15

Источник: Демонстрационная версия ЕГЭ—2013 по физике.

17. Ма­лень­кий гру­зик, за­креплённый на пру­жи­не жёстко­стью 80 Н/м, со­вер­ша­ет гар­мо­ни­че­ские ко­ле­ба­ния. Гра­фик за­ви­си­мо­сти ко­ор­ди­на­ты x этого гру­зи­ка от вре­ме­ни t изоб­ражён на ри­сун­ке. Ка­ко­ва масса гру­зи­ка? (Ответ дайте в грам­мах.)

За­да­ние 4 № 6336

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка Из гра­фи­ка на­хо­дим, что пе­ри­од ко­ле­ба­ний равен Найдём массу груза:

 

 

 

Ответ: 50

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 06.05.2014 ва­ри­ант ФИ10701.

18. Ма­лень­кий гру­зик мас­сой 25 г, за­креплённый на пру­жи­не, со­вер­ша­ет гар­мо­ни­че­ские ко­ле­ба­ния. Гра­фик за­ви­си­мо­сти ко­ор­ди­на­ты x этого гру­зи­ка от вре­ме­ни t изоб­ражён на ри­сун­ке. Ка­ко­ва жёсткость пру­жи­ны? (Ответ дайте в Н/м.)

За­да­ние 4 № 6371

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка Из гра­фи­ка на­хо­дим, что пе­ри­од ко­ле­ба­ний равен Найдём жёсткость пру­жи­ны:

 

 

 

Ответ: 62,5

62,5

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 06.05.2014 ва­ри­ант ФИ10702.

19. Гид­ро­аку­стик, на­хо­дя­щий­ся на ко­раб­ле, пе­ре­го­ва­ри­ва­ет­ся по рации с мат­ро­сом, на­хо­дя­щим­ся на лодке. Во время раз­го­во­ра мат­рос на­но­сит удар га­еч­ным клю­чом по кор­пу­су своей лодки. Звук от этого удара гид­ро­аку­стик сна­ча­ла слы­шит через рацию, а через 10 се­кунд — через свою гид­ро­аку­сти­че­скую ап­па­ра­ту­ру. Счи­тая, что вто­рой звук рас­про­стра­ня­ет­ся в воде со ско­ро­стью 1500 м/с, най­ди­те рас­сто­я­ние между ко­раблём и лод­кой. Ответ при­ве­ди­те в ки­ло­мет­рах.

За­да­ние 4 № 6640

Ре­ше­ние.

Счи­тая, что сиг­нал по рации при­хо­дит почти мгно­вен­но, найдём рас­сто­я­ние, ко­то­рое про­хо­дит звук от лодки до ко­раб­ля:

 

Ответ: 15.

Ответ: 15

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 12.12.2014 Ва­ри­ант ФИ10301.

20. Гид­ро­аку­стик, на­хо­дя­щий­ся на ко­раб­ле, пе­ре­го­ва­ри­ва­ет­ся по рации с мат­ро­сом, на­хо­дя­щим­ся на лодке. Рас­сто­я­ние между ко­раб­лем и лод­кой со­став­ля­ет 7,5 км. Во время раз­го­во­ра мат­рос на­но­сит удар га­еч­ным клю­чом по кор­пу­су своей лодки. Звук от этого удара гид­ро­аку­стик сна­ча­ла слы­шит через рацию, а затем — через свою гид­ро­аку­сти­че­скую ап­па­ра­ту­ру. Счи­тая, что вто­рой звук рас­про­стра­ня­ет­ся в воде со ско­ро­стью 1500 м/с, най­ди­те время между уда­ра­ми, ко­то­рые слы­шит гид­ро­аку­стик. (Ответ дайте в се­кун­дах.)

За­да­ние 4 № 6679

Ре­ше­ние.

Счи­тая, что сиг­нал по рации при­хо­дит почти мгно­вен­но, найдём время, за ко­то­рое звук про­хо­дит рас­сто­я­ние от лодки до ко­раб­ля:

 

 

Ответ: 5.

Ответ: 5

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 12.12.2014 Ва­ри­ант ФИ10302.

21. Ча­сто­та соб­ствен­ных малых вер­ти­каль­ных ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка равна 6 Гц. Какой ста­нет ча­сто­та таких ко­ле­ба­ний, если массу груза пру­жин­но­го ма­ят­ни­ка уве­ли­чить в 4 раза? Ответ при­ве­ди­те в гер­цах.

За­да­ние 4 № 6757

Ре­ше­ние.

Ча­сто­та соб­ствен­ных ко­ле­ба­ний пру­жин­но­го ма­ят­ни­ка вы­чис­ля­ет­ся по фор­му­ле Сле­до­ва­тель­но, при уве­ли­че­нии массы груза в че­ты­ре раза ча­сто­та ко­ле­ба­ний умень­шит­ся в два раза, зна­чит, ча­сто­та ко­ле­ба­ний ста­нет рав­ной 3 Гц.

 

Ответ: 3 Гц.

Ответ: 3

Источник: СтатГрад: Ди­а­гно­сти­че­ская ра­бо­та по фи­зи­ке 06.02.2015 Ва­ри­ант ФИ10402.

22. Груз на длин­ной лёгкой пру­жи­не со­вер­ша­ет ко­ле­ба­ния с ча­сто­той 0,5 Гц. Пру­жи­ну раз­ре­за­ли на 4 рав­ные части и при­кре­пи­ли к одной из ча­стей тот же груз. Чему стал равен пе­ри­од ко­ле­ба­ний по­лу­чив­ше­го­ся пру­жин­но­го ма­ят­ни­ка? (Ответ дайте в се­кун­дах.)

За­да­ние 4 № 7281

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка про­пор­ци­о­на­лен пе­ри­о­ду ко­ле­ба­ний груза, ко­то­рый опре­де­ля­ет­ся вы­ра­же­ни­ем

.

При по­сле­до­ва­тель­ном со­еди­не­нии пру­жин, общая жест­кость по­лу­ча­ет­ся из фор­му­лы: . От­сю­да сле­ду­ет, что жест­кость 1/4 части ис­ход­ной пру­жи­ны равна 4k. Уве­ли­че­нии жест­ко­сти пру­жи­ны в 4 раза при­во­дит к умень­ше­нию пе­ри­о­да ко­ле­ба­ний в два раза, а ча­сто­та, яв­ля­ясь об­рат­ной пе­ри­о­ду ве­ли­чи­ной, в свою оче­редь долж­на уве­ли­чить­ся в два раза и ста­нет рав­ной 1 Гц. Тогда пе­ри­од ко­ле­ба­ний по­лу­чив­ше­го­ся ма­ят­ни­ка будет равен 1 с.

 

Ответ: 1 с

Ответ: 1

Источник: СтатГрад: Тренировочная ра­бо­та по физике 05.10.2015 Ва­ри­ант ФИ10103

23. Груз на длин­ной лёгкой пру­жи­не со­вер­ша­ет ко­ле­ба­ния с ча­сто­той 1 Гц. Пру­жи­ну раз­ре­за­ли на 9 рав­ных ча­стей и при­кре­пи­ли к одной из ча­стей тот же груз. Чему стала равна ча­сто­та ко­ле­ба­ний по­лу­чив­ше­го­ся пру­жин­но­го ма­ят­ни­ка? (Ответ дайте в гер­цах.)

За­да­ние 4 № 7313

Ре­ше­ние.

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка про­пор­ци­о­на­лен пе­ри­о­ду ко­ле­ба­ний груза, ко­то­рый опре­де­ля­ет­ся вы­ра­же­ни­ем

.

При по­сле­до­ва­тель­ном со­еди­не­нии пру­жин, общая жест­кость по­лу­ча­ет­ся из фор­му­лы: . От­сю­да сле­ду­ет, что жест­кость 1/9 части ис­ход­ной пру­жи­ны равна 9k. Уве­ли­че­нии жест­ко­сти пру­жи­ны в 9 раз при­во­дит к умень­ше­нию пе­ри­о­да ко­ле­ба­ний в 3 раза, а ча­сто­та, яв­ля­ясь об­рат­ной пе­ри­о­ду ве­ли­чи­ной, в свою оче­редь долж­на уве­ли­чить­ся в 3 раза.

 

Ответ: 3 Гц

Ответ: 3

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 05.10.2015 Ва­ри­ант ФИ10104

24. 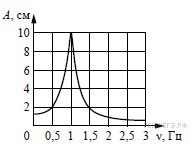На ри­сун­ке изоб­ра­же­на за­ви­си­мость ам­пли­ту­ды уста­но­вив­ших­ся ко­ле­ба­ний ма­ят­ни­ка от ча­сто­ты вы­нуж­да­ю­щей силы (ре­зо­нанс­ная кри­вая). Ча­сто­та вы­нуж­да­ю­щей силы вна­ча­ле была равна 0,5 Гц, а затем стала равна 1,0 Гц.

Во сколь­ко раз из­ме­ни­лась при этом ам­пли­ту­да уста­но­вив­ших­ся вы­нуж­ден­ных ко­ле­ба­ний ма­ят­ни­ка?

За­да­ние 4 № 7850

Ре­ше­ние.

Как видно из гра­фи­ка ам­пли­ту­да уве­ли­чи­лась с 2 см до 10 см, т. е. в 5 раз.

Ответ: в 5 раз.

Ответ: 5

Источник: ЕГЭ по фи­зи­ке 02.04.2016. До­сроч­ная волна

25. Гиря мас­сой 2 кг под­ве­ше­на на сталь­ной пру­жи­не и со­вер­ша­ет сво­бод­ные ко­ле­ба­ния вдоль вер­ти­каль­но на­прав­лен­ной оси Ox, ко­ор­ди­на­та x цен­тра масс гири, вы­ра­жен­ная в мет­рах, из­ме­ня­ет­ся со вре­ме­нем по за­ко­ну Чему равна ки­не­ти­че­ская энер­гия гири в на­чаль­ный мо­мент вре­ме­ни? (Ответ вы­ра­зи­те в джо­у­лях.)

За­да­ние 4 № 8429

Ре­ше­ние.

По­сколь­ку ко­ор­ди­на­та цен­тра масс гири ме­ня­ет­ся по за­ко­ну

 

 

ско­рость цен­тра масс гири ме­ня­ет­ся со­глас­но

 

 

В на­чаль­ный мо­мент ско­рость гири равна 2 м/с, а её ки­не­ти­че­ская энер­гия

 

 

Ответ: 4 Дж

Ответ: 4

26. Ма­те­ма­ти­че­ский ма­ят­ник с пе­ри­о­дом ко­ле­ба­ний Т от­кло­ни­ли на не­боль­шой угол от по­ло­же­ния рав­но­ве­сия и от­пу­сти­ли без на­чаль­ной ско­ро­сти (см. ри­су­нок). Через какое время (в долях пе­ри­о­да) после этого ки­не­ти­че­ская энер­гия ма­ят­ни­ка в пер­вый раз до­стиг­нет ми­ни­му­ма? Со­про­тив­ле­ни­ем воз­ду­ха пре­не­бречь.

За­да­ние 4 № 8430

Ре­ше­ние.

По­сколь­ку ма­ят­ник от­пу­сти­ли с ну­ле­вой на­чаль­ной ско­ро­стью, по­ло­же­ние на­чаль­но­го от­кло­не­ния со­от­вет­ству­ет мак­си­маль­но­му от­кло­не­нию. За время, рав­ное пе­ри­о­ду, ма­ят­ник успе­ет от­кло­нить­ся в про­ти­во­по­лож­ную сто­ро­ну, после чего вер­нет­ся в на­чаль­ное по­ло­же­ние. Ми­ни­маль­ной ки­не­ти­че­ской энер­гии со­от­вет­ству­ет по­ло­же­ние мак­си­маль­но­го от­кло­не­ния. Впер­вые ма­ят­ник ока­жет­ся в нем через по­ло­ви­ну пе­ри­о­да.

 

Ответ: 0,5

Ответ: 0,5

0,5

27. Ма­те­ма­ти­че­ский ма­ят­ник с пе­ри­о­дом ко­ле­ба­ний Т от­кло­ни­ли на не­боль­шой угол от по­ло­же­ния рав­но­ве­сия и от­пу­сти­ли с на­чаль­ной ско­ро­стью, рав­ной нулю (см. ри­су­нок). Через какое время (в долях пе­ри­о­да) после этого по­тен­ци­аль­ная энер­гия ма­ят­ни­ка в пер­вый раз вновь до­стиг­нет мак­си­му­ма? Со­про­тив­ле­ни­ем воз­ду­ха пре­не­бречь.

За­да­ние 4 № 8431

Ре­ше­ние.

По­сколь­ку ма­ят­ник от­пу­сти­ли с ну­ле­вой на­чаль­ной ско­ро­стью, по­ло­же­ние на­чаль­но­го от­кло­не­ния со­от­вет­ству­ет мак­си­маль­но­му от­кло­не­нию. За время, рав­ное пе­ри­о­ду, ма­ят­ник успе­ет от­кло­нить­ся в про­ти­во­по­лож­ную сто­ро­ну и вер­нуть­ся в ис­ход­ное по­ло­же­ние. Мак­си­маль­ная по­тен­ци­аль­ная энер­гии у ма­ят­ни­ка в по­ло­же­ни­ях мак­си­маль­но­го от­кло­не­ния. Таким об­ра­зом, по­тен­ци­аль­ная энер­гия ма­ят­ни­ка в пер­вый раз вновь до­стиг­нет мак­си­му­ма через по­ло­ви­ну пе­ри­о­да.

 

Ответ: 0,5

Ответ: 0,5

0,5

28. Ма­те­ма­ти­че­ский ма­ят­ник с пе­ри­о­дом ко­ле­ба­ний Т от­кло­ни­ли на не­боль­шой угол от по­ло­же­ния рав­но­ве­сия и от­пу­сти­ли с на­чаль­ной ско­ро­стью рав­ной нулю (см. ри­су­нок). Через какое время (в долях пе­ри­о­да) после этого ки­не­ти­че­ская энер­гия ма­ят­ни­ка во вто­рой раз до­стиг­нет мак­си­му­ма? Со­про­тив­ле­ни­ем воз­ду­ха пре­не­бречь.

За­да­ние 4 № 8432

Ре­ше­ние.

По­сколь­ку ма­ят­ник от­пу­сти­ли с ну­ле­вой на­чаль­ной ско­ро­стью, по­ло­же­ние на­чаль­но­го от­кло­не­ния со­от­вет­ству­ет мак­си­маль­но­му от­кло­не­нию. За время, рав­ное пе­ри­о­ду, ма­ят­ник успе­ет от­кло­нить­ся в про­ти­во­по­лож­ную сто­ро­ну, после чего вер­нет­ся в ис­ход­ное по­ло­же­ние. Мак­си­маль­ной ки­не­ти­че­ской энер­гии со­от­вет­ству­ет по­ло­же­ние рав­но­ве­сия. Впер­вые ма­ят­ник ока­жет­ся в нем через чет­верть пе­ри­о­да. А во вто­рой раз ки­не­ти­че­ская энер­гия до­стиг­нет мак­си­маль­но­го зна­че­ния через три чет­вер­ти пе­ри­о­да, когда ма­ят­ник будет воз­вра­щать­ся.

 

Ответ: 0,75

Ответ: 0,75

 

Поделиться:

Воспользуйтесь поиском по сайту: