 |
Методы расчета и анализа индексов цен.
|
|
|
|
Ведущая роль в статистическом изучении динамики цен принадлежит индексному методу. Сравнение цен одного товара осуществляется с помощью индивидуального (однотоварного) индекса цен:
pi1
ip = pi0
(1)
где p0, p1 - цены на товар в базисном и текущем периоде.
Индекс средних цен применяется при изучении изменения цен товарных групп, цен одного товара по различным территориям и субрынкам:
pi1  pi1qi1
pi1qi1  pi0qi0
pi0qi0  pi1qi1
pi1qi1  qi1
qi1
ip = = * =: (2)
pi0  qi1
qi1  qi0
qi0  pi0qi0
pi0qi0  qi0
qi0
_
где p - средняя цена товарной группы (товара по территориям, субрынкам);
pi, qi - цена и количество проданного i - го вида товара (товара на i - й территории
или i - м субрынке), i=l, n.
Товары должны быть достаточно однородными, чтобы их количество поддавалось суммированию.
Денежные расходы населения на покупку товаров определяются двумя составляющими: уровнем цен на отдельные виды товаров и структурой продажи. Различаются два вида структурных сдвигов в продаже: отражающие изменение качества товара и вызывающие только изменение средней цены. К последним относится перераспределение товарной массы по территориям, субрынкам, а также негативный процесс «вымывания» из ассортимента дешевых товаров, пользующихся спросом населения. Статистика изучает этот процесс с помощью системы индекса средних цен:
| Индекс средних цен (переменного состава) | = | Индекс цен постоянного (фиксированного) состава | . | Индекс влияния структурных сдвигов на динамику средних цен |
 pi1qi1
pi1qi1  qi1
qi1  pi1qi1
pi1qi1  pi0qi1
pi0qi1  qi1
qi1
: = *: (3)
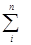 pi0qi0
pi0qi0 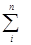 qi0
qi0 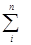 pi0qi1
pi0qi1 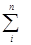 pi0qi0
pi0qi0 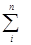 qi0
qi0
Так как
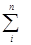 pi1qi1
pi1qi1 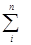 qi1
qi1 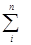 pi1qi1
pi1qi1 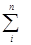 pi1qi1
pi1qi1
: = = (4)
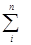 pi0qi0
pi0qi0 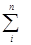 qi0
qi0 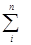 pi0qi0 *
pi0qi0 * 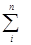 qi1
qi1 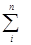 pi0qi1
pi0qi1
 qi0
qi0
то формулу (3) можно записать в следующем виде:
 pi1qi1
pi1qi1  pi1qi1
pi1qi1  pi0qi1
pi0qi1
= * (5)
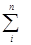 pi0qi1
pi0qi1 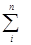 pi1qi1
pi1qi1 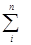 pi0qi1
pi0qi1
Пример.
Имеются цена и количество проданного магазином товара. Оценить динамику цены каждого сорта, среднюю цену за каждый квартал, а также определить влияние изменения индивидуальных цен и перераспределения продаж между сортами товара на изменение средних цен.
|
|
|
Расчет индекса средних цен
| Сорт | Цена, | тыс. руб. | Количест | во, шт | Товаро | оборот, | млн. | руб. | Индивиду | ||||
| товара | I квартал pi0 | II квартал pi1 | I квартал qi0 | II квартал qi1 |
pi0qi0 |
pi1qi1 |
pi0qi1 | pi1qi0 | альный индекс цен ip | ||||
| А | 40 | 80 | 500 | 200 | 20 | 16 | 8 | 40 | 2,0 | ||||
| Б | 50 | 70 | 300 | 600 | 15 | 42 | 30 | 21 | 1,4 | ||||
| В | 60 | 90 | 200 | 200 | 12 | 18 | 12 | 18 | 1,5 | ||||
| Итого | 1000 | 1000 | 47 | 76 | 50 | 79 | |||||||
Во второй части таблицы рассчитаны товарооборот базисного и текущего кварталов, индивидуальные индексы цен и условный товарооборот каждого сорта: выручка магазина при условии продажи товаров во II квартале по ценам I квартала. Средняя цена товара в I квартале составляла 47 тыс. руб. (47 млн. руб./1 тыс. шт.), во II квартале - 76 тыс. руб. Система индексов имеет вид:
76 1000 76 50 1000
47 1000 50 47 1000
1,61=1,52*1,06
Если бы произошедшие изменения цен не сопровождались структурным перераспределением продаж, то средняя цена товара выросла бы в 1,52 раза, а только изменение структуры продаж вызвало бы рост средней цены на 6%. Одновременное воздействие двух факторов увеличило среднюю цену продаж на 61%.
Основной формой индекса цен для совокупности разнородных товаров является агрегатный индекс. Цены различных товаров (например, конфет и компьютеров) складывать бессмысленно. Несуммируемость элементов совокупности преодолевается путем взвешивания каждой цены по количеству проданных товаров. Сумма произведений цен товаров на их количество составляет товарооборот совокупности товаров. Чтобы выявить непосредственно изменение цен, необходимо зафиксировать показатели количества на одном из уровней:
|
|
|
базисного периода времени (формула Ласпейреса)
 pi1qi0
pi1qi0
IpЛ = (6)
 pi0qi0
pi0qi0
или текущего периода времени (формула Пааше)
 pi1qi1
pi1qi1
IpП= (7)
 pi0qi1
pi0qi1
Четкость интерпретации, экономический смысл и удобство практического расчета формулы Ласпейреса сделали ее самой популярной в мире для расчета индекса потребительских цен, который показывает, во сколько раз изменились бы потребительские расходы в текущем периоде по сравнению с базисным, если бы при изменении цен уровень потребления оставался прежним. Такой расчет корректен при отсутствии значительных количественных и качественных изменений в структуре потребления (во времени и по территории, если индекс рассчитывается для нескольких регионов).
Изучение динамики розничных цен (например, для получения дефлятора, позволяющего рассчитать стоимостные показатели от четного периода в сопоставимых ценах) должно быть максимально приближено к совокупности товаров, произведенных в отчетном периоде. Результат расчета по формуле Пааше показывает, во сколько раз сумма фактических затрат населения на покупку товаров больше (меньше) суммы денег, которую население должно было бы заплатить за эти же товары, если бы цены оставались на уровне базисного периода.
Ограниченными возможностями регистрации цен объясняется использование различных модификаций формул Ласпейреса и Пааше:
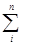 ippi1qi0
ippi1qi0
IpЛ = (8)
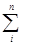 pi0qi0
pi0qi0
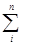 pi1qi1
pi1qi1
IpП= (9)
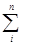 (1/ip)*pi0qi1
(1/ip)*pi0qi1
Статистическим анализом доказано, что в долговременном аспекте формула Пааше занижает реальное изменение цен вследствие общественной отрицательной корреляции (относительный вес товара падает, если цена его возрастает), а в случае долгосрочных и международных сопоставлений разница между индексами, взвешенными разными способами, составляет несколько процентов (до 30-50%). Значения индексов, вычисленных по формулам Ласпейреса и Пааше, совпадают лишь в случае почти невозможного на практике совпадения структуры товарной массы базисного и отчетного периодов. Установлено, что различия числовых значений этих индексов могут определяться тремя факторами: вариацией индивидуальных индексов цен (Vip), объемов (Viq) товаров и коэффициентом корреляции (rpq), измеряющим стохастическую связь между этими индивидуальными индексами. В целом зависимость между индексами имеет вид:
|
|
|
IpП / IpЛ = 1+ rpq* Vip * Viq (10)
Vip = sip / IpЛ; sip = 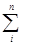 (ip - IpЛ)
(ip - IpЛ)  *pi0qi0 (11)
*pi0qi0 (11)
 pi0qi0
pi0qi0
Viq = siq / IqЛ; siq =  (iq- IqЛ)
(iq- IqЛ)  * pi0qi0 где iq = q1/q0; (12)
* pi0qi0 где iq = q1/q0; (12)
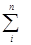 pi0qi0
pi0qi0
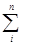 (ip - IpЛ)(iq- IqЛ) pi0qi0
(ip - IpЛ)(iq- IqЛ) pi0qi0
rpq =: (sip * siq) (13)
(ковариация) 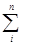 pi0qi0
pi0qi0
Так как Vip и Viq положительны, то знак выражения IpП / IpЛ зависит от знака rpq, таким образом IpП > IpЛ в случае, если цены и количество товаров имеют тенденцию в одном направлении (rpq >0), т. е. в условиях диктата поставщика. При рынке доминирующего спроса, разнообразии товаров, конкуренции IpП < IpЛ (рост цен вызывает относительное снижение объема покупок).
Пример.
По условиям предыдущего примера сделаем необходимые расчеты (конечно, трех уровней недостаточно для достоверной оценки вариации, в данном случае это упрощает расчеты примера).
Расчет показателей связи индексов
| Сорт | ip - IpЛ | (ip - IpЛ)  *
* pi0qi0 *
* pi0qi0
| iq | iq- IqЛ | (iq- IqЛ)  *
* pi0qi0 *
* pi0qi0
|
| А | 2,0-1,68=0,32 | 2,048 | 0,4 | 0,4-1,06=-0,66 | 8,712 |
| Б | 1,4-1,68=-0,28 | 1,176 | 2,0 | 2,0-1,06= 0,94 | 13,254 |
| В | 1,5-1,68=0,18 | 0,389 | 1,0 | 1,0-1,06=-0,06 | 0,043 |
| ИТОГО | -0,14 | 3,613 | - | 0,22 | 22,009 |
IpЛ = 1,68; IqЛ = 1,06;
sip = 3,613/47=0,277; siq = 22,009/47=0,684;
Vip = 0,277/1,68=0,165; Viq = 0,684/1,06=0,646;
rpq =-0,903; IpП / IpЛ =0,9.
Разница в значениях индексов в основном определяется взаимным влиянием изменений цен и количества, в значительной степени - вариацией количественных изменений и незначительно - вариацией цен.
Доказано, что наилучший линейный индекс лежит между индексами, вычисленными по формулам Ласпейреса и Пааше. Зарубежные статистики пытались найти компромиссную формулу.
Формула Эджворта - Маршалла:
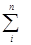 pi1((q1+q0)/2)
pi1((q1+q0)/2)
IЭ-М= (14)
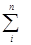 pi0((q1+q0)/2)
pi0((q1+q0)/2)
Формула (14) улавливает сдвиги в структуре покупок, но при вязана к условной структуре товарооборота, не характерной ни для одного реального периода, не имеет прямого экономического смысла. Ее расчет встречает препятствия в сборе материалов, как и расчет по формуле Пааше.
Наиболее удачным компромиссом многие экономисты считают «идеальный» индекс Фишера:
IФ = IpП * IpЛ (15)
который оценивает не только набор товаров базисного периода по ценам текущего, но и набор товаров текущего периода по ценам базисного. Применяется в случае трудностей с выбором весов или значительного изменения структуры весов.
|
|
|
Разновидностью розничных цен являются цены на продукты массового (общественного) питания. Они образуются на базе розничных или оптовых цен на продукты, покупаемые предприятиями массового питания с добавлением наценки, возмещающей издержки на переработку продуктов и дающей прибыль. Непосредственная регистрация цен продукции массового питания практически невозможна из-за большого разнообразия ее состава и отсутствия стабильной единицы измерения. Поэтому для расчета индекса цен на продукцию массового питания исчисляют индекс цен на израсходованные продукты и товары, проданные на предприятиях массового питания, и индекс ценовых факторов наценки (Inp). Последний, в свою очередь, состоит из двух индексов: индекса норм наценок (т. е. процента наценки к цене продукта) и индекса изменения самих цен:
 n1p1q1
n1p1q1  n1p1q1
n1p1q1  n0p1q1
n0p1q1
= * (16)
 n0p0q1
n0p0q1  n0p1q1
n0p1q1  n0p0q1
n0p0q1
где n - норма наценки товара;
k - число i - x разновидностей товаров.
Так как расход продуктов в производстве продукции массового питания учитывается в стоимостных единицах, то для расчета используется формула среднего гармонического индекса:
 n1p1q1
n1p1q1
Inp = (17)
 (1/inp)n1p1q1
(1/inp)n1p1q1
где inp = in * ip = n1p1 / n0p0 (18)
Формула индекса цен массового питания имеет вид:
 p1q1 +
p1q1 +  n1p1q1
n1p1q1  p1q1 +
p1q1 +  n1p1q1
n1p1q1
Ip = = (19)
 p0q1 +
p0q1 +  n0p0q1
n0p0q1  (1/ip) p1q1 +
(1/ip) p1q1 +  (1/inp)n1p1q1
(1/inp)n1p1q1
Индексы при систематическом расчете из года в год образуют индексные ряды. Различают базисные ряды (цены каждого года сравниваются с ценами года, принятого за базу) и цепные (характеризующие изменение цен по сравнению с предыдущим годом). Веса индексов ряда могут быть постоянными (на уровне одного года), и тогда произведение цепных индексов даст базисный индекс. Применение системы переменных весов (по количеству товаров отчетного года) в индексном ряду цен порождает ошибку при переходе от цепных индексов к базисным и обратно (произведение Iцеп > Iбаз), так как позитивна корреляция между текущим изменением цен и прошлым изменением количества проданных товаров. Эта ошибка мала, если корреляционная связь между изменением цен и количества проданного товара незначительна. На практике система цепных индексов (достоинство - сокращает период сравнения, ограничивает круг несопоставимых товаров) используется для коротких периодов, затем осуществляется поправка по формуле базисного периода, так как за длительный период ошибка накапливается.
Численные значения индексов, рассчитанных по различным формулам на основе одних и тех же данных, отличаются и порой значительно, особенно в годы резких изменений уровня цен и связанного с этим изменения структуры спроса. Отдать предпочтение одной формуле трудно: разные цели диктуют применение индексных форм, имеющих разный экономический смысл. Отказ от концепции единственного индекса цен в пользу концепции системы индексов позволит дать обобщающую характеристику и оценку основных причин изменения розничных цен. Но поскольку все же индексный метод не универсален, а отражает лишь тенденцию движения цен, то нельзя требовать большей определенности от рассчитанных индексов. Кроме того, на чистоту результатов огромное влияние оказывает достоверность исходных материалов, особенно ошибка выборки, степень представительности товаров, включенных в расчет.
|
|
|
|
|
|


