Главная | Обратная связь | Поможем написать вашу работу!

Тема 11. Развертки поверхностей

Развертки поверхностей. Условные развертки не развертывающихся поверхностей.

Тема 12. Аксонометрические проекции

Прямоугольные изометрические проекции. Прямоугольные диметри-ческие проекции. Косоугольные аксонометрические проекции. Позиционные и метрические задачи в аксонометрии.

Контрольные работы

Контрольные работы по начертательной геометрии представляют собой эпюры (чертежи), которые выполняются по мере изучения курса.

Задания на контрольные работы индивидуальные. Они представлены в вариантах. Студент выполняет вариант задания, указанный преподавателем во время установочной сессии, либо вариант, номер которого соответствует сумме трех последних цифр его кода (номера студенческого билета или зачетной книжки). Если, например, учебный код студента 028133, то он во всех контрольных работах выполняет седьмой вариант задания. Каждая контрольная работа представляется на рецензию в полном объеме.

Если работа не зачтена, преподаватель в рецензии указывает, какую часть контрольной работы надо переделать или же выполнить всю контрольную работу вновь. На повторную рецензию следует представить всю контрольную работу полностью. К выполнению следующей контрольной работы приступить, не ожидая ответа на предыдущую.

Контрольные работы представляются строго в сроки, указанные в учебном графике.

Эпюры контрольных работ выполняются на листах чертежной бумаги формата A3 (297x420 мм) или А4 (210x297 мм). На расстоянии 5 мм от линии обреза листа проводится рамка поля чертежа. С левой стороны линия рамки проводится от линии обреза листа на расстоянии 20 мм. В правом нижнем углу формата, вплотную к рамке, помещается основная надпись. Ее размеры и пример заполнения приведены на рис. 1.

Рис. 1. Основная надпись

Задания к эпюрам берутся в соответствии с вариантами из таблиц. Чертежи заданий вычерчиваются в заданном масштабе и размещаются с учетом наиболее равномерного размещения всего эпюра в пределах формата листа.

Эпюры выполняются с помощью чертежных инструментов: вначале карандашом с последующей обводкой некоторых построений красной пастой шариковой ручки. При обводке карандашом или пастой характер и толщина линий берутся в соответствии с ГОСТ 2.303-68. Все видимые линии - основные сплошные толщиной s = 0,8...1,0 мм. Линии построений и линии проекционной связи должны быть сплошными тонкими толщиной от s /2 до s /3 мм. Линии центров и осевые – штрихпунктирной линией толщиной от s /2 до s /3 мм. Линии невидимых контуров показывают штриховыми линиями. На это следует обратить внимание при выполнении всех контрольных работ, имея при этом в виду, что заданные плоскости и поверхности непрозрачны. Все основные вспомогательные построения должны быть сохранены.

Все надписи, как и отдельные обозначения, в виде букв и цифр на эпюре, должны быть выполнены стандартным шрифтом размером 3,5 и 5 в соответствии с ГОСТ 2.304-81*.

Первая страница контрольных работ должна быть выполнена на листе ватмана формата А4 и оформлена по образцу, приведенному на рис. 2.

Задания к контрольным работам

На установочной сессии студентам в зависимости от специальности выдается перечень задач, составляющих контрольные работы, в соответствии с рабочей программой специальности.

Задача 1

Построить линию пересечения плоскостей, заданных треугольниками ABC и EDK, показать видимость. Определить натуральную величину треугольника ABC. Данные для своего варианта взять из табл. 1. Пример выполнения задачи 1 приведен на рис. 3.

Указания к решению задачи. В левой половине листа формата A3 намечаются оси координат и из табл. 1 согласно своему варианту берутся координаты точек А, В, С, D, Е, К – вершин треугольников. Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями. Линии пересечения треугольников строятся по точкам пересечения сторон одного треугольника с другим или по точкам пересечения каждой из сторон одного треугольника с другим порознь. Такую линию можно построить, используя и вспомогательные секущие проецирующие плоскости.

Видимость сторон треугольника определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными основными линиями, невидимые следует показать штриховыми линиями.

Министерство образования и науки Российской Федерации Саратовский государственный технический Университет Кафедра «Начертательная геометрия и компьютерная графика» НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Контрольная работа №____

Выполнил: студент гр._________ Ф.И.О.________________

САРАТОВ 20__

Рис. 2. Пример выполнения титульного листа

Таблица 1.

№	X_A	Y_A	Z_A	X_B	Y_B	Z_B	X_C	Y_C	Z_C	X_D	Y_D	Z_D	X_E	Y_E	Z_E	X_K	Y_K	Z_K
1	117	90	9	52	25	79	0	83	48	68	110	85	135	19	36	14	52	0
2	120	90	10	50	25	80	0	85	50	70	110	85	135	20	35	15	50	0
3	115	90	10	52	25	80	0	80	45	65	105	80	130	18	35	12	50	0
4	120	92	10	50	20	75	0	80	46	70	115	85	135	20	32	10	50	0
5	117	9	90	52	79	25	0	48	83	68	85	110	135	36	19	14	0	52
6	115	7	85	50	80	25	0	50	85	70	85	110	135	40	20	15	0	50
7	120	10	90	48	82	20	0	52	82	65	80	110	130	38	20	15	0	52
8	116	8	88	50	78	25	0	46	80	70	85	108	135	36	20	15	0	52
9	115	10	92	50	80	25	0	50	85	70	85	110	135	35	20	15	0	50
10	18	10	90	83	79	25	135	48	83	67	85	110	0	36	19	121	0	52
11	20	12	92	85	80	25	135	50	85	70	85	110	0	35	20	120	0	52
12	15	10	85	80	80	20	130	50	80	70	80	108	0	35	20	120	0	50
13	16	12	88	85	80	25	130	50	80	75	85	110	0	30	15	120	0	50
14	18	12	85	85	80	25	135	50	80	70	85	110	0	35	20	120	0	50
15	18	90	10	83	25	79	135	83	48	67	110	85	0	19	36	121	52	0
16	18	40	75	83	117	6	135	47	38	67	20	0	0	111	48	121	78	86
17	18	79	40	83	6	107	135	38	47	67	0	20	0	48	111	121	86	78
18	117	75	40	52	6	107	0	38	47	135	0	20	68	48	111	15	86	78
19	117	40	75	52	107	6	47	38	135	20	0	0	68	111	48	15	78	86
20	120	38	75	50	108	5	0	54	40	135	20	0	70	110	50	15	80	85
21	122	40	75	50	110	8	0	50	40	140	20	0	70	110	50	20	80	85
22	20	40	10	85	110	80	135	48	48	70	20	85	0	110	35	120	80	0
23	20	10	40	85	80	110	135	48	48	70	85	20	0	35	110	120	0	80
24	117	40	9	52	111	79	0	47	48	68	20	85	135	111	36	14	78	0
25	117	9	40	52	79	111	0	48	47	68	85	20	135	36	111	14	0	78
26	18	40	9	83	111	79	135	47	48	67	20	85	0	111	36	121	78	0
27	18	9	46	83	79	111	135	48	47	67	85	20	0	36	111	121	0	78

Рис. 3. Пример решения задачи 1.

Определяется натуральная величина треугольника ABC, для чего:

1. В плоскости проводят прямую уровня (горизонталь h ≡ CR).

2. Плоскопараллельным перемещением треугольник ABC

приводится в положение проецирующей плоскости (h₁'^x₁₂), в результате прямая CR становится фронтально-проецирующей прямой, а плоскость ABC - фронтально-проецирующей плоскостью.

3. Вращением вокруг фронтально-проецирующей прямой, проходящей через точку В, преобразуем плоскость треугольника ABC в плоскость уровня (горизонтальную, когда он будет параллелен горизонтальной плоскости проекций).

4. Строится горизонтальная проекция A₁"B₁"C₁", которая является натуральной величиной треугольника.

В треугольнике ABC следует показать и линию MN пересечения его с треугольником EDK.

Все вспомогательные построения должны быть обязательно показаны на чертеже в виде тонких линий, а линия пересечения треугольников MN обведена красной пастой.

Задача 2

Построить проекции пирамиды, основанием которой является треугольник ABC, а ребро SA определяет высоту h пирамиды. Данные для своего варианта взять из табл. 2. Пример решения задачи приведен на рис. 4.

Указания к решению задачи. В левой половине листа формата A3 намечают оси координат и из табл. 2 согласно своему варианту берут координаты точек А, В и С вершин треугольника ABC. По координатам строится двухкартинный эпюр треугольника.

В плоскости треугольника ABC проводят линии уровня (горизонталь h и фронталь f). В точке А восстанавливается перпендикуляр к плоскости треугольника, для чего на плоскости П₂ проводят перпендикуляр к фронтали (f₂), на П₁ - к горизонтали (h₁). Для определения натуральной величины ребра SA следует применить способ вращения, который подробно рассмотрен в пояснениях к решению задачи 5 (рис.7).

На направлении отрезка SA берут произвольную точку S', определяют натуральную величину отрезка S'A, откладывают заданную высоту пирамиды h и находят проекции вершины пирамиды S (S₁, S₂). Строятся ребра пирамиды.

Способом конкурирующих точек определяется их видимость. Видимые ребра пирамиды следует показать основными сплошными линиями, невидимые - штриховыми линиями. Все вспомогательные построения необходимо сохранить на эпюре и показать их тонкими линиями.

Таблица 2

№	А			В			С			h
№	x	y	z	x	y	z	x	y	z	h
1	117	90	9	52	25	79	0	83	8	85
2	120	90	10	50	25	80	0	85	50	85
3	115	90	10	52	25	80	0	80	45	85
4	120	92	10	50	20	75	0	80	46	85
5	117	9	90	52	79	25	0	48	83	85
6	115	7	85	50	80	25	0	50	85	85
7	120	10	90	48	82	20	0	52	82	85
8	116	8	88	50	78	25	0	46	80	85
9	115	10	92	50	80	25	0	50	85	85
10	18	10	90	83	79	25	135	48	83	85
11	20	12	92	85	80	25	135	50	85	85
12	15	10	85	80	80	20	130	50	80	85
13	16	12	88	85	80	25	130	50	80	80
14	18	12	85	85	80	25	135	50	80	80
15	18	90	10	83	25	79	135	83	48	80
16	18	40	75	83	117	6	135	47	38	80
17	18	75	40	83	6	107	135	38	47	80
18	117	75	40	52	6	107	0	38	47	80
19	117	40	75	52	107	6	0	47	38	80
20	120	38	75	50	108	5	0	45	40	80
21	122	40	75	50	110	8	0	50	40	85
22	20	40	10	85	110	80	135	48	48	80
23	20	10	40	85	80	110	135	48	48	85
24	117	40	9	52	111	79	0	47	48	80
25	117	9	40	52	79	111		48	47	85
26	18	40	9	83	111	79	135	47	48	80
27	18	9	40	83	79	111	135	48	47	80

Задача 3

Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из табл. 3. Пример выполнения задачи приведен на рис. 4.

Указания к решению задачи. В оставшейся правой половине листа намечаются оси координат и из табл. 3 согласно своему варианту берутся координаты точек А, В, С и D вершин пирамиды и координаты точек E, K, G и U вершин многоугольника нижнего основания призмы. Высота призмы для всех вариантов равна 85 мм. По этим данным строятся проекции многогранников.

Таблица 3

№	X_A	Y_A	Z_A	X_B	Y_B	Z_B	X_C	Y_C	Z_C	X_D	Y_D	Z_D	X_E	Y_E	Z_E	X_K	Y_K	Z_K	X_G	Y_G	Z_G	X_U	Y_U	Z_U
1	141	75	0	122	14	77	87	100	40	0	50	40	100	50	0	74	20	0	16	20	0	55	95	0
2	0	70	0	20	9	77	53	95	40	141	45	40	40	50	0	67	20	0	125	20	0	86	95	0
3	0		0	20		77	53	110	40	141	55	40	40	50	0	67	20	0	125	20	0	86	95	0
4	0	68	0	20	7	77	53	93	40	141	143	40	40	50	0	67	20	0	125	20	0	86	95	0
5	0	75	0	20	14	77	53	100	40	141	50	40	40	50	0	67	20	0	125	20	0	86	95	0
6	0	82	0	20	21	77	53	112	40	141	57	40	40	50	0	67	20	0	125	20	0	86	95	0
7	0	85	0	20	24	77	53	115	40	141	60	40	40	50	0	67	20	0	125	20	0	86	95	0
8	0	90	0	20	29	77	53	120	40	141	65	40	40	50	0	67	20	0	125	20	0	86	95	0
9	0	85	0	15	30	80	55	120	40	141	60	40	40	50	0	67	20	0	125	20	0	86	95	0
10	141	70	0	122	9	77	87	95	40	0	45	40	100	50	0	74	20	0	16	20	0	55	95	0
11	141	80	0	122	19	77	87	110	40	0	55	40	100	50	0	74	20	0	16	20	0	55	95	0
12	141	68	0	122	7	77	87	93	40	0	43	40	100	50	0	74	20	0	16	20	0	55	95	0
13	141	82	0	122	21	77	87	112	40	0	57	40	100	50	0	74	20	0	16	20	0	55	95	0
14	141	85	0	122	24	77	87	115	40	0	60	40	100	50	0	70	20	0	16	20	20	55	95	0
15	141	90	0	122	14	77	87	120	40	0	65	40	100	50	0	74	20	0	16	20	0	55	95	0
16	135	75	0	116	14	77	81	100	40	0	50	40	100	50	0	74	20	0	16	20	0	55	95	0
17	145	75	0	126	34	77	91	100	40	0	50	40	100	50	0	74	20	0	16	20	0	55	95	0
18	145	95	0	120	10	77	87	120	40	0	70	60	100	50	0	74	20	0	16	20	0	55	95	0
19	145	70	0	122	20	80	90	95	40	0	70	45	100	50	0	74	20	0	16	20	0	55	95	0
20	145	65	0	122	20	70	85	100	40	0	68	47	100	50	0	74	20	0	16	20	0	55	95	0
21	122	14	77	141	75	0	87	100	40	0	50	40	105	55	0	80	15	0	20	20	0	55	95	0
22	120	15	80	140	75	0	85	100	45	0	50	45	105	55	0	80	15	0	20	20	0	55	95	0
23	125	20	80	140	75	0	85	100	45	0	55	45	98	52	0	76	20	0	18	22	0	57	95	0
24	140	70	0	120	15	80	85	95	50	0	50	45	100	50	0	75	22	0	20	20	0	60	90	0
25	140	65	0	115	20	75	80	90	40	0	50	40	100	45	0	75	17	0	22	25	0	60	95	0
26	135	65	0	120	20	75	80	90	40	0	55	45	100	48	0	70	15	0	20	27	0	65	95	0
27	135	60	0	115	20	80	85	90	40	0	50	40	100	43	0	70	20	0	20	20	0	60	90	0

Призма своим основанием стоит на плоскости уровня, горизонтальные проекции ее вертикальных ребер преобразуются в точки. Грани боковой поверхности призмы представляют собой отсеки горизонтально проецирующих плоскостей.

Линия взаимного пересечения многогранников представляет собой пространственную замкнутую ломаную линию. Для построения линии пересечения сначала находят ее вершины, а затем в определенном порядке соединяют их отрезками прямых. Вершины этой линии могут быть определены как точки пересечения ребер одного многогранника (пирамиды) с гранями другого (призмы). Соединяя каждые пары таких точек, принадлежащих одним и тем же граням, отрезками прямых, получаем линию пересечения многогранников.

Видимыми являются только те стороны многоугольника пересечения, которые принадлежат видимым граням многогранников. Их следует показать сплошными основными линиями красной пастой. Все вспомогательные построения на эпюре сохранить и показать их тонкими линиями.

ПРИМЕЧАНИЕ. Задаче 3 уделить особое внимание. Все построения на чертеже тщательно проверить. Допущенные ошибки приводят к неправильному решению следующих задач 4, 5 «Построение развертки многогранников».

Задача 4

Построить развертку прямой призмы. Показать на развертке линию пересечения ее с пирамидой. Исходные данные для построений взять из задачи 3. Пример выполнения задачи приведен на рис. 5.

Указания к решению задачи. Разверткой поверхности многогранника называется плоская фигура, полученная при совмещении с плоскостью чертежа всех его граней, такое совмещение возможно только после предварительных разрезов поверхности по некоторым ребрам.

На листе ватмана формата A3 (297 ĥ 420 мм) строится развертка прямой призмы.

Для построения развертки прямой призмы поступают следующим образом:

а) проводят горизонтальную прямую (при решении задач 3 и 4 на одном листе прямая может являться продолжением оси х);

б) от произвольной точки G этой прямой откладывают отрезки GU,
UE, EK, KG, равные длинам сторон основания призмы;

в) из точек G, U, E, К, G восстанавливают перпендикуляры и на них откладывают величины, равные высоте призмы. Полученные точки соединяют прямой. Прямоугольник GG'G'G является разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, Е, К проводят перпендикуляры;

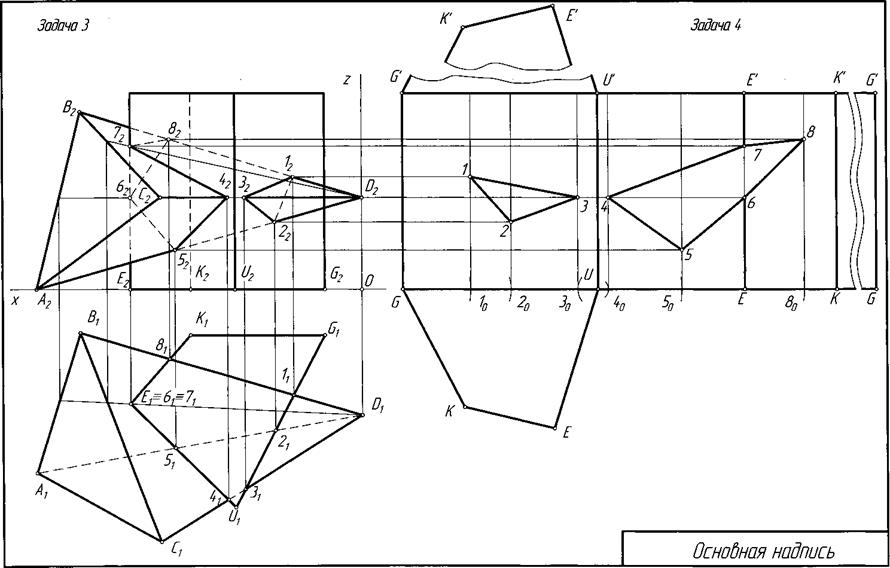
Рис. 5. Пример компоновки листа при решении задач 3 и 4.

г) для получения полной развертки поверхности призмы к развертке боковой поверхности пристраивают многоугольники ее оснований.

Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломаных линий 1-2-3 и 4-5-6-7-8 пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке поступаем так: на отрезке GU от точки G вправо откладываем отрезок Gl₀, равный отрезку G₁1₁ (проекция на горизонтальную плоскость) (рис. 5). Из точки 1₀ восстанавливаем перпендикуляр к отрезку GU и на нем откладываем аппликату z точки 1. Аналогично строят и находят остальные точки. Найденные точки соединяют замкнутыми ломаными.

Ребра многогранника на развертке обвести сплошными основными линиями, линии пересечения призмы с пирамидой обвести красной пастой, а все вспомогательные построения выполнить сплошными тонкими линиями.

Задача 5

Построить развертку пирамиды. Показать на развертке линию пересечения ее с призмой. Исходные данные (призму и пирамиду) для построений взять из задачи 3. Пример выполнения задачи приведен на рис. 8 и 9.

Указания к решению задачи. Развертка трехгранной пирамиды состоит из треугольных граней, каждая из которых строится как треугольник по трем заданным сторонам.

Для построения развертки пирамиды необходимо предварительно определить натуральные величины всех ее ребер любым из методов преобразования чертежа (способом вращения, способом замены плоскостей проекций или методом прямоугольного треугольника).

На рис. 6 показано построение истинного вида отрезка АВ с помощью прямоугольного треугольника, одним катетом которого служит проекция прямой на одной из плоскостей проекций, а другим - разность расстояний конечных точек отрезка до этой плоскости. На эпюре показана проекция А₁' В₁', которая является натуральной величиной отрезка АВ.

Метод вращения можно рассматривать как частный случай плоскопараллельного перемещения, когда все точки пространства и, следовательно, погруженной в него фигуры, перемещаются по дугам окружностей, центры дуг принадлежат одной прямой, называемой осью вращения, а плоскости дуг перпендикулярны к оси. На рис. 7 показано построение истинной величины отрезка АВ вращением вокруг оси, перпендикулярной плоскости П₁. Если повернуть точку А вокруг оси ^ П₁, то ее горизонтальная проекция А₁ повернется на такой же угол и займет положение А₁', а ее фронтальная проекция будет перемещаться по прямой, перпендикулярной оси вращения. Зная положение горизонтальной проекции А₁', строим фронтальную проекцию А₂' по линии проекционной связи А₁' А₂'. При таком вращении положение точки В остается неизменным, а отрезок АВ приведен к положению линии уровня

(фронтали). Таким образом, преобразованная проекция А₂' В₂' является натуральной величиной отрезка АВ.

Определяют последовательно натуральные величины всех ребер пирамиды (кроме ребра CD, которое является горизонталью, поэтому его проекция на плоскость П₁ есть ни что иное как натуральная величина).

На листе ватмана формата A3 (297х 420 мм) строится развертка пирамиды, здесь же выполняются все построения по нахождению натуральных величин ребер пирамиды. На ребрах и гранях пирамиды (на развертке) определяют вершины пространственной ломаной пересечения пирамиды с призмой. Последовательно соединяют эти точки, с учетом их принадлежности отдельным граням пирамиды, по описанию в задаче 3.

На рис. 4, 5, 8, 9 приведены варианты размещения задач 3, 4, 5 в зависимости от содержания контрольных работ для разных специальностей.

Задача 6

На трехпроекционном чертеже построить недостающие проекции сквозного отверстия в сфере заданного радиуса R. Вырожденная (фронтальная) проекция сквозного отверстия представлена четырехугольником. Координаты проекций точек А, В, С и D (вершин четырехугольника) заданы в табл. 4. Пример выполнения задачи приведен на рис.10.

Указания к решению задачи. Намечаются оси координат с началом координат в центре листа формата A3. Строятся проекции сферы заданного радиуса R с центром в точке О. Определяются по заданным координатам проекции точек А, В, С и D (вершин четырехугольника) сквозного отверстия на сфере и строится многоугольник - вырожденная проекция линии сквозного отверстия.

Вначале определяются характерные точки линии сквозного отверстия: точки на экваторе, главном меридиане, наиболее удаленные и ближайшие точки поверхности сферы к плоскостям проекций. Далее задача сводится к определению недостающих проекций точек поверхности сферы и определению видимости проекции отверстия. Очертание сферы и вырожденную проекцию сквозного сечения обвести сплошными основными линиями, невидимые участки поверхности и линии выреза показать линиями невидимого контура (штриховыми). Все вспомогательные построения на чертеже сохранить и обвести тонкими линиями.

Таблица 4

№	О			А		В		С		D		R
№	x	y	z	x	z	x	z	x	z	x	z	R
1	70	58	62	118	35	56	95	45	95	45	35	46
2	70	60	60	118	35	56	95	44	95	44	35	46
3	70	60	58	120	35	58	95	44	95	44	35	48
4	70	60	58	120	36	56	94	42	94	42	36	48
5	69	58	60	116	36	58	94	45	94	45	36	47
6	72	60	58	116	36	60	92	42	92	42	36	47
7	72	58	60	120	34	60	92	42	92	42	34	48
8	72	58	58	122	34	60	90	40	90	40	34	45
9	74	62	60	122	34	55	90	40	90	40	34	45
10	69	58	60	20	36	81	94	94	94	94	36	47
11	74	62	58	20	36	80	92	94	92	94	36	47
12	72	62	62	20	35	80	92	92	92	92	35	48
13	72	60	62	22	35	82	90	92	90	92	35	48
14	70	60	60	18	35	82	90	90	90	90	35	48
15	70	60	58	18	34	82	94	92	94	92	34	50
16	72	62	58	20	34	84	94	96	94	96	34	50
17	70	62	60	18	32	84	90	96	90	96	32	50
18	68	60	60	20	32	86	92	95	92	95	32	50
19	68	58	62	20	32	86	92	95	92	95	32	50
20	70	58	62	18	32	86	94	90	94	90	32	52
21	70	60	58	118	35	60	95	45	95	45	35	52
22	70	62	62	120	36	60	92	42	92	42	36	50
23	68	62	60	120	34	62	92	42	92	42	34	50
24	68	62	58	122	35	62	90	40	90	40	35	52
25	68	60	58	120	36	60	90	42	90	42	36	52
26	70	60	60	120	35	60	92	44	92	44	35	52
27	70	58	60	120	32	62	92	45	92	45	32	50

Задача 7

Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения - взаимно перпендикулярные проецирующие скрещивающиеся прямые. Данные для своего варианта взять из табл. 5.

Указания к решению задачи. Вправой половине листа намечают оси координат и из табл. 5 берут согласно своему варианту величины, которыми задаются поверхности конуса вращения и цилиндра вращения.

Определяют центр (точка К) окружности радиуса R основания конуса вращения в горизонтальной координатной плоскости. На вертикальной оси на расстоянии h от плоскости уровня и выше ее определяют вершину конуса вращения.

Осью цилиндра вращения является фронтально-проецирующая прямая, проходящая через точку Е, основаниями цилиндра - окружности радиуса R₁. Образующие цилиндра имеют длину, равную 3 R₁, и делятся пополам фронтальной меридиональной плоскостью конуса вращения.

С помощью вспомогательных плоскостей определяют точки пересечения очерковых образующих одной поверхности с другой и промежуточные точки линии пересечения поверхностей. Проводя вспомогательную секущую фронтальную меридиональную плоскость конуса вращения, определяют точки пересечения главного меридиана (очерковых образующих) конуса вращения с параллелью (окружностью) проецирующего цилиндра. Выбирая горизонтальную секущую плоскость, проходящую через ось цилиндра вращения, определяют две точки пересечения очерковых образующих цилиндра с поверхностью конуса.

Высшую и низшую, а также промежуточные точки линии пересечения поверхности находят с помощью вспомогательных плоскостей уровня (горизонтальных плоскостей). По точкам строят линию пересечения поверхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.

Очертания поверхностей вращения следует обвести с учетом видимости основными сплошными и штриховыми линиями, а линию пересечения поверхностей - красной пастой. Все основн

⇐ Предыдущая 123 Следующая ⇒

Воспользуйтесь поиском по сайту: