 |
Электрические процессы в коаксиальном кабеле
|
|
|
|
Основные уравнения электромагнитного поля – уравнения Максвелла. Запишем закон полного тока:
(1)
т.е. циркуляция вектора напряженности магнитного поля 
вдоль произвольного замкнутого контура L равна полному току I.
Найдем напряженность магнитного поля, продифференцируем выражение (1), получим:
(2)
Замкнутый контур L (длина окружности проводника) равен:
L=2πr, (3)
где r – расстояние от центра проводника.
Тогда уравнение примет вид:
(4)
Способность коаксиальной пары пропускать широкий спектр частот конструктивно обеспечивается коаксиальным расположением внутреннего и внешнего проводников. Особенности распространения электромагнитной энергии по коаксиальной паре обусловлено возможностью уплотнения в широком спектре частот и ставят высокочастотные связи в преимущественное положение по сравнению с низкочастотными. Взаимодействие электромагнитных полей внутреннего и внешнего проводников коаксиальной пары таково, что внешнее поле равно нулю.
Рассмотрим раздельно электрическое и магнитное поле коаксиальной пары.
Результирующее магнитное поле коаксиальной пары представлено на рис. 3, где показаны также напряженности магнитного поля Наφ и Нбφ каждого проводника (а и б) в отдельности. В металлической толщине проводника а магнитное поле Наφ возрастает, а вне его уменьшается по закону:
Наφ=I/2πr, (5)
где r‑расстояние от центра проводника.
Поле Нбφ проводника б изображено в соответствии с законами электродинамики, согласно которым внутри полого цилиндра магнитное поле отсутствует, а вне его выражается таким же уравнением, как и для сплошного проводника:
|
|
|
Нбφ=I/2πr, (6)
где r‑расстояние от центра полого проводника. Поэтому при определении внешних магнитных полей коаксиального кабеля параметр r для проводников а и б принимается одинаковый и исчисляется от центра проводников (нулевой точки).
Рис. 3
Учитывая, что токи в проводниках а и б равны по величине и обратны по знаку, магнитные поля внутреннего и внешнего проводников Наφ и Наφ в любой точке пространства вне коаксиальной пары также будут равны по величине и направлены в разные стороны. Следовательно, результирующее магнитное поле вне коаксиальной пары по принципу суперпозиции, равно нулю:
Нφ= Наφ+ Нбφ= I/2πr+(-I/2πr)=0. (7)
Таким образом, силовые линии магнитного поля коаксиальной пары располагаются в виде концентрических окружностей внутри нее; вне коаксиальной пары магнитное поле отсутствует. Электрическое поле будет также замыкаться внутри коаксиальной пары по радиальным направлениям между проводниками а и б, поэтому за ее пределами оно равно нулю.
На рис. 4 представлены электромагнитные поля симметричной и коаксиальной пар. Как видно, электромагнитное поле коаксиальной пары полностью замыкается внутри ее, а силовые линии электромагнитного поля симметричной пары действуют на довольно значительном от нее расстоянии. Отсутствие внешнего электромагнитного поля обусловливает основные достоинства коаксиальных кабелей: высокая защищенность от взаимных и внешних помех, малые тепловые потери в соседних цепях и оболочках, однокабельная система связи.
Рис. 4. Электромагнитное поле симметричной (а) и коаксиальной (б) цепей
Рассмотрим действие поверхностного эффекта (скин–эффект) и эффекта близости в коаксиальных парах и определим характер распространения плотности токов в проводниках при различных частотах.
Распределение плотности тока в проводнике определяется лишь действием поверхностного эффекта (рис. 5). Силовые линии внутреннего магнитного поля, пересекая толщину проводника, наводят в ней вихревые токи, направленные согласно закону Ленца против вращения рукоятки буравчика. Как показано на рис. 5, вихревые токи Iв.т в центре проводника имеют направление, обратное движению основного тока, протекающего по проводнику, а на периферии их направления совпадают. В результате взаимодействия вихревых токов с основным происходит такое перераспределение тока по сечению проводника, при котором плотность тока возрастает к поверхности проводника. Это явление, называемое поверхностным эффектом (скин–эффектом), увеличивается с возрастанием частоты тока, магнитной проницаемости, проводимости и диаметра проводника.
|
|
|
Рис. 5
При достаточно высокой частоте ток протекает лишь по поверхности проводника, что вызывает увеличение его активного сопротивления.
Во внешнем проводнике плотность тока увеличивается в направлении к ее внутренней поверхности. Это объясняется воздействием поля внутреннего проводника. Если бы внутреннего проводника не было, то переменный ток, проходя по внешнему проводнику, вследствие поверхностного эффекта вытеснялся бы на внешнюю поверхность. При наличии внутреннего проводника плотность тока увеличивается на внутренней поверхности внешнего проводника.
Рассмотрим процесс перераспределения плотности тока во внешнем проводнике б за счет воздействия внутреннего проводника а. Как показано на рис. 6, переменное магнитное поле, создаваемое током проводника а, наводит в металлической толще полого проводника б вихревые токи Iв.т.
Рис. 6 Рис. 7
На внутренней поверхности проводника б вихревые токи совпадают по направлению с основным током (I+Iв.т), а наружной поверхности они движутся против последнего (I-Iв.т). В результате ток в проводнике б перераспределяется таким образом, что его плотность возрастает в направлении к внутренней поверхности. Следовательно, токи в проводниках а и б как бы смещаются и концентрируются на взаимно обращенных поверхностях проводников (рис. 7). Чем выше частота тока, тем сильнее эффект смещения тока на внешнюю поверхность проводника а и внутреннюю поверхность проводника б.
|
|
|
По-другому поверхностный эффект можно объяснить как проникновение электромагнитного поля в толщину проводника. Причем чем выше частота, тем меньше глубина проникновения поля в металл.
Эквивалентной глубиной проникновения θ называется глубина проникновения в толщу проводника, при которой поле (ток) уменьшается (затухает) в е=2,718 раз. С увеличением частоты передаваемого тока глубина проникновения резко уменьшается. В результате энергия сосредотачивается внутри коаксиального кабеля в диэлектрике, а проводники задают лишь направление распространения волн электромагнитной энергии.
Мешающее электромагнитное поле высокой частоты, создаваемое соседними цепями передачи или другими источниками помех, действует на внешний проводник коаксиальной пары, также будут распространяться не по всему сечению кабеля, а лишь по его наружной поверхности. Таким образом, внешний проводник коаксиальной пары выполняет две функции:
1. является обратным проводником цепи передачи;
2. защищает (экранирует) передачу, ведущуюся по кабелю, от мешающих влияний.
Рис. 8
Из рис. 8 видно, что основной ток передачи концентрируется на внутренней поверхности проводника б коаксиальной пары, а ток помех–на наружной стороне внешнего проводника. Как основной ток, так и ток помех проникают в толщу проводника лишь на глубину, определяемую коэффициентом вихревых токов. Причем чем выше частота, тем больше отдаляются друг от друга основной ток и ток помех, и следовательно, кабель лучше защищен от действия посторонних помех.
Таким образом, в отличии от всех других типов кабеля, для защиты которых от помех требуются специальные меры (симметрирование, экранирование и т.д.), защита коаксиальных кабелей на высоких частотах обеспечивается самой их конструкцией.
Из изложенного следует, что основные преимущества коаксиального кабеля (малое затухание и высокая помехозащищенность), особенно ярко проявляются в высокочастотной части передаваемого спектра частот.
|
|
|
При постоянном токе и на низких частотах, когда ток практически проходит по всему сечения проводников, достоинства этого кабеля пропадают. Больше того, коаксиальная цепь, как несимметричная относительно других цепей и земли (параметры ее проводников а и б различны), в низком диапазоне частот по защищенности от помех уступает симметричным кабелям.
4. Электромагнитное поле коаксиальной цепи
Запишем уравнения Максвелла в дифференциальной форме:
Где:
ρ – плотность стороннего электрического заряда (в единицах СИ – Кл/м³)
j – плотность электрического тока (в единицах СИ – А/м²)
E – напряжённость электрического поля (в единицах СИ – В/м)
H – напряжённость магнитного поля (в единицах СИ – А/м)
D – электрическая индукция (в единицах СИ – Кл/м²)
B – магнитная индукция (в единицах СИ – Тл = Вб/м²= кг·с-2·А-1)
Так как энергия сосредоточивается внутри коаксиального кабеля в диэлектрике, а проводники задают лишь направление распространению электромагнитных волн и этот диэлектрик не является проводящим материалом, то токи утечки в них отсутствуют. Также, в обычных условиях, материалы из которых может быть изготовлен диэлектрик, электрически нейтральны, поэтому положим:
(11)
Для того чтобы получить дифференциальное уравнение второго порядка описывающее изменение электрического и магнитного поля во времени и в пространстве продифференцируем первое уравнение из системы уравнений (9) по времени:
Из первого уравнения системы (8) получим:
Подставим сюда второе уравнение из системы (10):
Подставим (14) в (12):
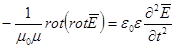
Так как:
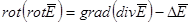
Из (11) следует, что grad[divE]=0
Подставим (18) в (17), а затем (17) в (16) получим:
Полученное выражение может быть преобразовано к следующему виду:
Произведем замену 
на v2. Получим:
Аналогичным образом, исключая вектор E из уравнений Максвелла можно получить волновое уравнение для вектора Н:
волновому уравнению подчиняется также скалярный φ и векторный a потенциалы.
Если коаксиальную пару расположить так, чтобы ее ось совпадала с осью z, то электромагнитное поле вследствие цилиндрической симметрии не будет зависеть от координаты φ. Кроме того, по физическим соображениям будет отсутствовать составляющая Нz–напряженность магнитного поля по оси z. Также отсутствует тангенциальная составляющая напряженности электрического поля Еφ и радиальная составляющая напряженности магнитного поля Нr.
|
|
|
Рис. 9
Таким образом, применительно к коаксиальной паре идеальной конструкции действуют лишь три составляющие электромагнитного поля: Er, Ez и Нφ (рис. 9).
Электрическое поле характеризуется двумя составляющими: радиальной Er и продольной Ez. Радиальная составляющая Er обуславливает наличие тока смещения в диэлектрике Iсм и совпадает по направлению с вектором плотности последнего. Продольная составляющая Ez вызывает ток проводимости Iпр в проводниках, направленных вдоль кабеля.
В результате волновые уравнения для коаксиальной пары будет иметь вид:
Если Ez=0 то система уравнений (23) примет вид:
Так как, для системы уравнений 1.18, векторы напряженности электрического и магнитного полей лежат в плоскости, перпендикулярной направлению распространения волны, то в волноводе распространяется поперечная электромагнитная волна или волна типа ТЕМ.
Электромагнитные волны – поперечные волны: векторы Е и Н поля волны лежат в плоскости, перпендикулярной к направлению распространения волны, т.е. к вектору ее скорости v в рассмотренной точке поля. В этом проще всего убедиться на примере плоской волны, распространяющейся вдоль положительного направления оси ОХ.
Векторы Е и Н и их проекции на оси координат не зависят от y и z:
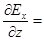
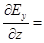
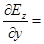
0 (25)
и
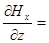
0 (26)
Из уравнений Максвелла (8,9) следует, что для поля плоской волны
0 (27)
и
0, (28)
т.е. Е 
и Н 
не зависят ни от координат, ни от времени. Поэтому для переменного поля плоской волны Е = Н =0 и векторы Е и Н перпендикулярны к направлению распространению волны:
Е= E 
j+E 
k (29)
и
H=H j+H k, где (30)
j и k – орты осей координат.
Для направляющих систем уравнения Максвелла наиболее часто применяются в цилиндрической системе координат:
(31)
Электромагнитное поле коаксиальной пары определяется уравнениями:
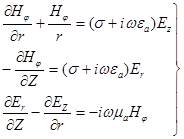(32)
|
|
|
