 |
Понятие систем счисления. Многочленная форма представления чисел. Преимущество позиционных систем счисления. Формы и методы представления чисел в памяти ЭВМ. Проблемы технической реализации.
|
|
|
|
Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления:
·даёт представления множества чисел (целых и/или вещественных);
·даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);
·отражает алгебраическую и арифметическую структуру чисел.
Например: 500 = 111110100 (в двоичной системе)
Наиболее часто употребляемыми в настоящее время позиционными системами являются:
·2 — двоичная (в дискретной математике, информатике, программировании);
·3 — троичная;
·8 — восьмеричная;
·10 — десятичная (используется повсеместно);
·12 — двенадцатеричная (счёт дюжинами);
·16 — шестнадцатеричная (используется в программировании, информатике);
·20 — двадцатеричная система счисления;
·60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).
Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
x = anPn + an -1 Pn -1 +... + a 1 P 1 + a 0 P 0 + a -1 P -1 +... + a-mP-m
Например в десятиричной системе: 103=1*102 + 0*101 + 3*100
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах
|
|
|
Основные достоинства любой позиционной системы счисления, это:
rпростота выполнения арифметических операций;
rограниченное количество символов, необходимых для записи любого числа;
rудобство для механического представления чисел.
Представление чисел в формате с фиксированной запятой. Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а "запятая" "находится" справа после младшего разряда, то есть вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А2 = = 111100002 будет храниться в ячейке памяти следующим образом:
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно
2n - 1.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно
А = 1*27 + 1*26 + 1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20 = 1*28 - 1 = 25510.
Диапазон изменения целых неотрицательных чисел чисел: от 0 до 255.
Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное - 1).
Для представления знаковых целых чисел используются три способа: 1) прямой код; 2) обратный код; 3) дополнительный код.
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — цифровая часть содержит двоичную запись числа, в знаковом разряде содержится 0. Например, для k = 8:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
|
|
|
В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Пример (при k = 8):

Обратный код отрицательных чисел: Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Пример (k = 8):

Дополнительный код отрицательных чисел Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:

Заметим, что ноль имеет два представления в прямом и обратном коде, а в дополнительном коде представление нуля единственно.
Например, при k = 8 обр(+1)=доп(+1)=1=00000001(2);
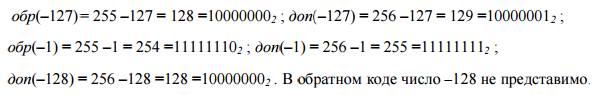
Представление вещественных чисел
Целые и дробные числа в совокупности называются вещественными числами.
Всякое вещественное число (X) можно записать в виде произведения мантиссы m и основания системы счисления р в некоторой целой степени n, которую называют порядком:
X = m · рn.
Например, число 25,324 можно записать в таком виде: 0,25324 · 102. Здесь m = 0,25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Плавающая запятая или плавающая точка - положение запятой в записи числа может изменяться.
Пример: 555,55 = 55555•10–2 = 0,55555•103 Любое число А может быть представлено в экспоненциальной форме: А = m • qn, где m – мантисса числа, q – основание системы счисления,n – порядок числа. Пример: 0,55555•103 Нормализованная форма числа. Чтобы привести к какому-то стандарту в представлении чисел с плавающей запятой условились представлять числа в нормализованной форме. При этом мантисса отвечает условию: она должна быть правильной дробью и иметь после запятой цифру, отличную от нуля. 1/n < | m | < 1 Пример:555,55 – естественная форма 0,55555•103 – нормализованная форма 0,55555 > 1/3 ~ 0,3333… 0,55555 < 1 Это касается и отрицательных чисел, т.к. мантисса в условии взята по модулю. Дробные числа занимают в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). Для записи таких чисел выделяются разряды для хранения: знака мантиссы, знака порядка, порядка числа мантиссы. 1-й байт 2-й байт 3-й байт 4-й байт
|
|
|
Пример: 0,14 = 0,00100011
0,14 < 1/2, поэтому старший разряд равен 0
0,14 < 1/4, поэтому следующий разряд также равен 0
0,14 > (1/8 = 0,125), поэтому следующий разряд равен 1
0,14 – 0,125 = 0,015
0,015 < (1/16 = 0,0625), поэтому следующий разряд равен 0
0,015 < (1/32 = 0,03125), поэтому следующий разряд равен 0
0,015 < (1/64 = 0,015625), поэтому следующий разряд равен 0
0,015 > (1/128 = 0,0078125), поэтому следующий разряд равен 1
0,015 – 0,0078125 = 0,0071875
0,0071875 > (1/256 = 0,00390625), поэтому следующий разряд равен 1
|
|
|


