Дифференциальные уравнения равновесия Эйлера

 

В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом dV с ребрами dx, dy и dz, расположенными параллельно осям координат х, у и г (рис. 2). Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на ускорение свободного падения g, т. е. равна gdm. Сила гидростатического давления на любую из граней параллелепипеда равна произведению гидростатического давления р на площадь этой грани. Будем считать, что давление р является функцией всех трех координат: р = f (х, у, z).

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. В противном случае происходило бы перемещение жидкости.

Рассмотрим сумму проекций сил на ось z. Сила тяжести направлена вниз, параллельно оси z. Поэтому при выбранном положительном направлении оси z (см. рис. 2) сила тяжести будет проектироваться на эту ось со знаком минус:

– g dm = – g dV = – g dx dy dz. (1)

Сила гидростатического давления действует на нижнюю грань параллелепипеда по нормали к ней, и ее проекция на ось z равна р dx dy. Если изменение гидростатического давления в данной точке в направлении оси z равно , то по всей длине ребра dz оно составит dz. Тогда гидростатическое давление на противоположную (верхнюю) грань равно (р + dz) и проекция силы гидростатического давления на ось z

- (р + dz) dx dy. (2)

Проекция равнодействующей силы давления на ось z

. (3)

Сумма проекций сил на ось г равна нулю, т. е.

(4)

или, учитывая, что объем параллелепипеда dx dy dz = dV ¹ 0 (величина, заведомо не равная нулю), получим

(5)

Проекции сил тяжести на оси х и у равны нулю. Поэтому сумма проекций сил на ось х

(6)

откуда после раскрытия скобок и сокращения находим

или . (7)

Соответственно для оси у

или . (8)

Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:

(9)

Уравнения (9) представляют собой дифференциальные уравнения равновесия Эйлера.

Для получения закона распределения давления во всем объеме покоящейся жидкости следует проинтегрировать систему уравнений (9). Интегралом этих уравнений является основное уравнение гидростатики, широко используемое в инженерной практике.

Основное уравнение гидростатики. Из уравнений (9) следует, что давление в покоящейся жидкости изменяется только по вертикали (вдоль оси z, рис. 2), оставаясь одинаковым во всех точках любой горизонтальной плоскости, так как изменения давлений вдоль осей х и у равны нулю. В связи с тем, что в этой системе уравнений частные производные и равны нулю, частная производная 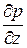может быть заменена на и, следовательно

. (10)

Отсюда

(11)

Разделив левую и правую части последнего выражения на и переменив знаки, представим это уравнение в виде

. (12)

Для несжимаемой однородной жидкости плотность постоянна и, следовательно

или . (13)

откуда после интегрирования получим

(14)

Для двух произвольных горизонтальных плоскостей 1 и 2 уравнение (14) выражают в форме

(15)

Уравнение (14) или (15) является основным уравнением гидростатики.

В уравнении (15): z₁ и z₂ — высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), a p₁ и р₂ – гидростатические давления в этих точках.

Член z в уравнении гидростатики (уравнение 14), представляющий собой высоту расположения данной точки над произвольно выбранной плоскостью сравнения, называется нивелирной высотой. Она, как и другой член этого уравнения , выражается в единицах длины, м.

Величину называют напором давления или пьезометрическим напором.

Следовательно, согласно основному уравнению гидростатики, для каждой точки покоящейся жидкости сумма нивелирной высоты и пьезометрического напора есть величина постоянная.

Члены основного уравнения гидростатики имеют определенный энергетический смысл. Так, выражение члена до сокращения характеризует удельную энергию, т. е. энергию, приходящуюся на единицу веса жидкости. Аналогичный энергетический смысл получает и нивелирная высота, если ее выражение [м] умножить и затем разделить на единицу веса жидкости.

Таким образом, нивелирная высо та z, называемая также геометрическим (высотным) напором, характеризует удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения (см. рис. 3), а пьезометрический напор – удельную потенциальную энергию давления в этой точке. Сумма указанных энергий, называемая полным гидростатическим напором, или просто статическим напором, равна общей потенциальной энергии, приходящейся на единицу веса жидкости.

Следовательно, основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.

 

Закон Паскаля

 

Рассмотрим, например, две частицы жидкости, из которых одна расположена в точке 1 внутри объема жидкости (рис. 3) – на высоте z от произвольно выбранной плоскости сравнения 0—0, а другая находится в точке 2 на поверхности жидкости – на высоте z_o от той же плоскости. Пусть р и p_o – давления в точках 1 и 2 соответственно. При этих обозначениях, согласно уравнению (15)

или . (1)

Уравнение (1) можно записать и в форме

или . (2)

Последнее уравнение является выражением закона Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается одинаково всем точкам ее объема.

 

Некоторые практические приложения основного уравнения гидростатики

 

Основное уравнение гидростатики, выражаемое часто в виде закона Паскаля, имеет ряд важных практических приложений; некоторые из них рассматриваются ниже.

 

Рис. 4. Условия равновесия в сообщающихся сосудах:

а – однородная жидкость; б – разнородные (несмешивающиеся) жидкости

Принцип сообщающихся сосудов и его использование. Пусть два открытых сообщающихся сосуда (рис. 4, а) заполнены жидкостью плотностью . Выберем произвольно плоскость сравнения 0–0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то, согласно уравнению (2), давление в данной точке

Если же считать точку А принадлежащей правому сосуду, то давление в ней

(, так как плоскость 0 – 0 проходит через точку А).

При равновесии для каждой точки давление одинаково в любом направлении (в противном случае происходило бы перемещение жидкости). Следовательно

или (1)

Аналогичный вывод может быть сделан для двух закрытых сообщающихся сосудов, в которых давления над свободной поверхностью жидкости одинаковы. Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и поперечного сечения сосудов. Этот принцип используется, в частности, для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стекол.

Если сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотности r ' (левый сосуд) и r " (правый сосуд), то при проведении плоскости сравнения 0–0 через границу раздела жидкостей (рис. 4, б) аналогично предыдущему получим

или . (2)

Отсюда следует, что в сообщающихся сосудах высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

Если сосуды заполнены одной жидкостью плотностью , но давления над уровнем жидкости в них неодинаковы и равны r ' (левый сосуд) и r " (правый сосуд), то

откуда разность уровней жидкости в сосудах

Это уравнение применяют при измерениях давлений или разностей давлений между различными точками с помощью дифференциальных U -образных манометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных аппаратах. Так, в непрерывно действующих сепараторах (рис. 5) смесь жидкостей различной плотности (эмульсия) непрерывно поступает в аппарат 1 по центральной трубе 2 и расслаивается в нем, причем более легкая жидкость плотностью r ' удаляется сверху через штуцер 3, а более тяжелая имеющая плотность r ", — снизу через U -образный затвор 4. Если принять, что уровень границы раздела фаз поддерживается на границе цилиндрической и конической частей аппарата и провести через эту границу плоскость сравнения 0 — 0, то необходимая высота гидравлического затвора, согласно уравнению (20), составит

(1)

При этом допускается, что давление над жидкостью внутри аппарата и на выходе из затвора одинаково.

Пневматическое измерение количества жидкости в резервуарах. Для контроля за объемом жидкости в каком-либо резервуаре 1, например подземном (рис. 6), в него помещают трубу 2, нижний конец которой доходит почти до днища резервуара. Давление над жидкостью в резервуаре равно р_о. По трубе 2 подают сжатый воздух или другой газ, постепенно повышая его давление, замеряемое манометром 3. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать сквозь жидкость, давление р, фиксируемое манометром, перестанет возрастать и будет равно, согласно уравнению (2)

откуда уровень жидкости в резервуаре

(1)

По величине и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

Гидростатические машины. На использовании основного уравнения гидростатики основана работа гидростатических машин, например гидравлических прессов (рис. 7), применяемых в пищевой промышленности для прессования и брикетирования различных материалов. Если приложить относительно небольшое усилие к поршню 1, движущемуся в цилиндре меньшего диаметра d₁, и создать давление р на поршень, то, согласно закону Паскаля, такое же давление р будет приходиться на поршень 2 в цилиндре большего диаметра d₂. При этом сила давления на поршень 1 составит

а сила давления на поршень 2

В результате поршень в цилиндре большего диаметра передаст силу давления, во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, во сколько поперечное сечение цилиндра 2 больше, чем цилиндра 1. Таким способом с помощью сравнительно небольших усилий осуществляют прессование материала 3, помещенного между поршнем 2 и неподвижной плитой 4.

Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех точках горизонтального дна сосуда одинаково, давление же на его боковые стенки возрастает с увеличением глубины погружения.

Гидростатическое давление р на уровне дна сосуда (см. рис. 3), как и для любой точки внутри жидкости, определяется уравнением (18г), но для всех точек дна величина () представляет собой высоту жидкости в сосуде. Обозначив последнюю через Н, получим

(1)

Таким образом, сила давления Р на горизонтальное дно сосуда не зависит от формы сосуда и объема жидкости в нем. При данной плотности жидкости эта сила определяется лишь высотой столба жидкости Н и площадью F дна сосуда:

или . (2)

Гидростатическое давление жидкости на вертикальную стенку сосуда изменяется по высоте. Соответственно сила давления на стенку также различна по высоте сосуда. Поэтому

(3)

где h – расстояние от верхнего уровня жидкости до центра тяжести смоченной площади F стенки.

В уравнении (3) выражение в скобках представляет собой гидростатическое давление в центре тяжести смоченной площади стенки. Поэтому сила давления на вертикальную стенку равна произведению ее смоченной площади на гидростатическое давление в центре тяжести смоченной площади стенки.

Точка приложения равнодействующей Р сил давления на стенку называется центром давления. Эта точка расположена всегда ниже центра тяжести смоченной площади. Если давление р_о передается жидкостью в одинаковой степени каждому элементу стенки, независимо от глубины его погружения, и, следовательно, равнодействующая сила этого давления приложена в центре тяжести стенки, то давление столба жидкости на стенку тем больше, чем глубже расположен соответствующий ее элемент. В результате, в частности, для вертикальной прямоугольной стенки центр давления расположен на расстоянии 2Н/3 от верхнего уровня жидкости.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: