Кинематическое исследование механизма

ВВЕДЕНИЕ

Теория механизмов и машин – наука, изучающая общие методы структурного и динамического анализа и синтеза различных механизмов, проектирование их схем, механику машин. Важно подчеркнуть, что излагаемые в теории механизмов и машин методы пригодны для проектирования любого механизма и не зависят от его технического назначения, а также физической природы рабочего процесса машины.

Студент должен изучить основные положения и методы ТММ, а также приобрести навыки в применении этих методов к исследованию и проектированию кинематических схем механизмов и машин разных типов.

Курсовое проектирование способствует закреплению, углублению и обобщению теоретических знаний, а также применению их к комплексному решению конкретной задачи по исследованию и расчёту механизма.

Кинематическое исследование механизма

1.1.Построение плана механизма

По исходным данным вычерчиваем кинематическую схему механизма в масштабе для восьми положений кривошипа.

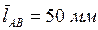Действительная длина ведущего звена На чертеже изобразим его отрезком звена . Тогда масштаб длины на плане механизма будет равен:

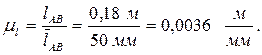
В этом масштабе вычерчиваем схему механизма. Размеры в мм остальных звеньев в выбранном масштабе определяются соответственно:

;

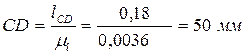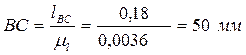
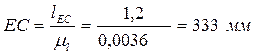
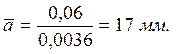
Выбираем произвольную точку А, изображаем в ней опору и от этой точки начинаем построение. По горизонтали откладываем межосевое расстояние 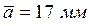, по вертикали расстояние и ставим точку D (опора). Из точки A радиусом 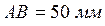описываем окружность, которая является траекторией движения точки B. Из точки D радиусом 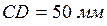описываем окружность, которая является траекторией движения точки C. Находим крайнее левое и крайнее правое положение ползуна Е. Для этого из точки D делаем засечки на горизонтальной прямой радиусами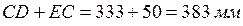

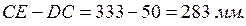
Делим окружность СD на восемь равных частей. Из соответствующих точек C делаем засечки радиуса 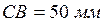на окружности 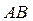. Соединив точки C и В, получим восемь положений звена 2 (шатуна CВ). Точки В соединяем с точкой А. Из точек С делаем засечки радиусом 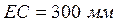до пересечения с горизонтальной прямой по которой движется звено 5 (поршень Е) и отмечаем точки Е.

Соединяя последовательно точки С₀, С₁,..., С₇ с соответствующими точками Е₀, Е₁,...., Е₇, получают кинематическую схему механизма в восьми положениях.

1.2. Построение планов скоростей

Скорость точки В:.

,

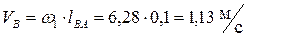где 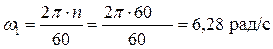- угловая скорость вращения кривошипа.

Вектор скорости точки В перпендикулярен кривошипу АВ.

Точка С принадлежит одновременно двум звеньям: звену 2 и 3. По теореме о сложении скоростей, скорость точки С равна геометрической сумме скорости точки В и скорости точки С в относительном вращении вокруг В:

,

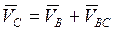где - вектор скорости точки С перпендикулярен СD.

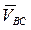- вектор скорости C в относительном вращении вокруг D, перпендикулярен ВC.

Выбираем на плоскости произвольную точку Р – полюс плана скоростей, которая является началом отсчета. Откладываем от точки Р вектор Pb, перпендикулярный звену АB, в направлении линейной скорости точки B. Длину вектора возьмем равной 63 мм. Тогда масштаб плана скоростей равен:

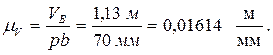
На плане скоростей через точку b проводим прямую, перпендикулярную к звену 2 механизма (это линия вектора 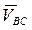). Через точку Р проводим прямую перпендикулярную шатуну DC (на ней лежит вектор скорости 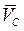). Пересечение этих двух прямых точка c – является концом вектора .

Скорость точки E.

,

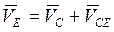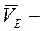вектор скорости точки E, находится на горизонтальной прямой.

– вектор скорости точки E в относительном движении вокруг C, перпендикулярен EC.

На плане скоростей через точку c проводим прямую, перпендикулярную к звену 4 механизма (это линия вектора ). Через точку Р проводим горизонтальную прямую (на ней лежит вектор скорости 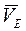). Пересечение этих двух прямых точка e – является концом вектора 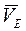. Строим планы скоростей для 8- и положений механизма, измеряем полученные отрезки. Модуль скорости определяем по равенству:

,

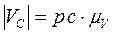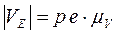
На плане скоростей находим середину векторов ab, cb. Ставим соответственно точки S ₂, S ₄. Вектора рs ₂, рs ₄определяют скорости центров масс звеньев 2 и 4. Результат заносим в таблицу 1.1

 

 

 

Таблица 1.1 – Скорости точек и угловые скорости звеньев

Скорости точек	0, 8
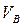
	1,13
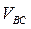
	1,8	0,807	0,66	0,66	0,87	1,13	1,36	1,78
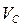
	2,1	1,45	1,13	0,904	0,68	0,65	0,84	1,45
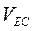
	2,1	0,56	0,48	0,85	0,69	0,50	0,56	0,45
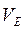
		1,37	0,94	0,45	0,096	0,29	0,72	1,45
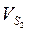
	1,4	1,2	1,07	0,97	0,81	0,73	0,71	0,97
	1,05	1,34	1,03	0,52	0,34	0,42	0,73	1,45
		4,48	3,6	3,7	4,8	6,28	7,55	9,9
	11,67	7,89	6,28	5,02	3,78	3,61	4,67	8,1
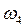
	1,75	0,47	0,4	0,71	0,58	1,42	0,48	0,38

1.3. Построение планов ускорений

Полное ускорение точки В складывается из двух составляющих: нормаль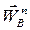ного ускорения и касательного ускорения :

,

где модули векторов равны:

;

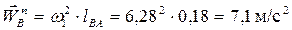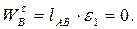
Вектор нормального ускорения направлен вдоль прямой АВ от точки В к центру А, вектор тангенциального ускорения - перпенди­кулярно прямой АВ. При 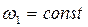угловое ускорение кривошипа и тангенциальная составляющая 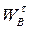ускорения точки В так­же равна нулю.

Приняв некоторую точку 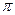за полюс плана ускорений отложим вектор, изображающий нормальное ускорение точки В, в виде отрезка ( 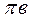=71 мм). Тогда масштаб ускорений найдется из соотношения:

.

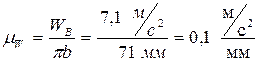Ускорение точки С:

,

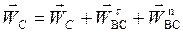где нормальное ускорение рассчитываем по формуле:

.

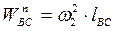Для положения 2: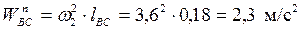

Значение скорости берем из таблицы 1.2. Вектор 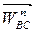должен быть направлен по линии ВС от точки С к точке В. Вектор 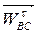известен только по направлению – перпендикулярен ВС.

Точка С принадлежит звену 3:

.

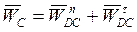где нормальное ускорение рассчитываем по формуле:

.

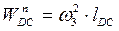Для положения 2:

Через точку b ранее построенного отрезка (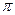 b) плана ускорений проводят линию, параллельную ВC и откладывают на ней отрезок 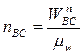, направленный от точки C к точке B. Это есть вектор относитель­ного нормального ускорения . Через конец этого вектора про­водят прямую перпендикулярно звену ВC (направление вектора 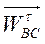). От полюса 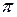откладываем отрезок 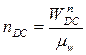, через конец вектора проводим прямую перпендикулярную этому отрезку (направление вектора ). Точку пересечении перпендикулярных прямых отмеча­ют буквой с. Отрезок 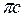изображает полное ускорение точки С, мо­дуль которого равен

.

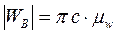Ускорение точки Е:

,

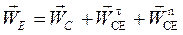где нормальное ускорение рассчитываем по формуле:

.

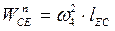Вектор 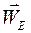лежит на горизонтальной прямой. Вектор 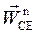направлен по звену 4 от точки Е к С. Расчетные значение нормальных ускорений точек C и Е, а также размеры в мм на плане ускорений приведены в таблице 1.2.

Через точку с на плане ускорений проводят линию, параллельную CЕ и откладывают на ней отрезок 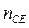, направленный от точки Е к точке С. Это есть вектор относитель­ного нормального ускорения 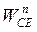. Через конец этого вектора про­водят прямую перпендикулярно звену CЕ (направление вектора 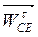), а через полюс 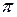проводят горизонтальную прямую (направление вектора 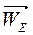) и точку их пересечения отмеча­ют буквой е. Отрезок 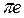изображает полное ускорение точки Е.

Измеряем полученные отрезки.

Модули ускорений точек Е и С определяем по формулам:

,

.

 

Полученные ускорения заносим в таблицу 1.3.

 

 

Таблица 1.2 – расчетные значения нормальных ускорений

 

Положение механизма
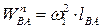
	7,1
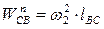
	2,3	10,3
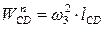
	7,1	3,9
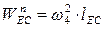
	0,2	0,26

Таблица 1.3 – модули ускорений

 

Положение механизма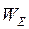
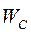
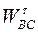
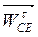
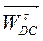
	5,1	7,20	2,3	5,8	3,0
	4,7	4,9	0,3	2,1	1,5

Рис. 1.1 Схема механизма

 

 

 

Рис.1.2. План скоростей

 

 

Рис.1.3. План ускорений

Диаграмма перемещений.

 

Необходимо построить диаграмму перемещений ползуна Е..

На оси абсцисс откладываем отрезок х, равный 240 мм который изображает угол од­ного поворота ведущего звена кривошипа АВ, равный 2π.

Масштаб угла поворота:

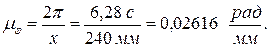
Масштаб времени:

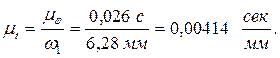
Разделим ось х на 8 равных частей.

Перемещение точки Е измеряем на плане механизма:

Е₀Е₁ =30мм; Е₀Е₂ =72мм; Е₀Е₃ =92мм; Е₀Е₄ =99мм; Е₀Е₅ =95мм; Е₀Е₆ =78мм; Е₀Е₇ =41 мм; Е₀Е₈ =0мм.

Действительное перемещение ползуна Е:

На диаграмме перемещений ход ползуна изобразим отрезком равным 100мм.

По оси у откладываем перемещения ползуна Е в масштабе:

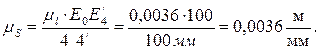
Размеры остальных точек рассчитаем:

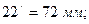
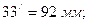
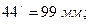
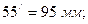
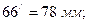
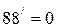
Соединяем плавной кривой полученные точки 1^/, 2^/ и т.д., получаем диаграмму перемещения выходного звена (поршня Е).

Поделиться:

Воспользуйтесь поиском по сайту: