Главная | Обратная связь | Поможем написать вашу работу!

Преобразование координат при векторном управлении

Структурная схема асинхронного двигателя во вращающейся системе координат содержит в качестве входных и выходных величин проекции соответствующих пространственных векторов на оси вращающейся системы координат. Эти величины являются величинами постоянного тока, что позволяет строить систему управления приводом так же, как систему управления электроприводом постоянного тока. Между тем, в реальной системе с трехфазным асинхронным двигателем напряжения и токи представляют собой трехфазные системы синусоидальных величин. Поэтому при построении системы управления электроприводом в нее должны быть введены преобразователи координат, осуществляющие преобразование величин постоянного тока во вращающейся системе координат в трехфазную систему величин в неподвижной системе координат и обратно.

Рассмотрим преобразования величин из одной системы координат в другую применительно к току статора (рис.2.4).

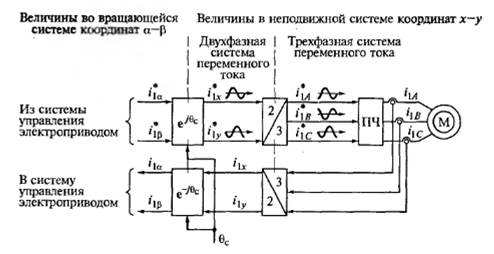
Рис.2.4 Структура преобразования координат при векторном управлении

Преобразования осуществляются в два этапа. В преобразователе канала, обратной связи трехфазная система синусоидальных величин преобразуется в двухфазную систему синусоидальных величин, а затем двухфазная система — в проекции пространственного вектора на оси вращающейся системы координат α-β, представляющие собой сигналы постоянного тока. В преобразователе прямого канала сначала из сигналов постоянного тока формируется двухфазная система переменных, а затем она трансформируется в трехфазную систему величин [10].

Для получения формулы преобразования трехфазной системы токов в двухфазную в неподвижной системе координат рассмотрим пространственный вектор тока статора в неподвижной системе координат.

где i_1A, i_1B, i_1C – мгновенные значения токов в обмотках статора.

С другой стороны, вектор I₁_x_-_y может быть представлен в виде суммы проекций на оси х и у неподвижной системы координат, об этом было рассказано в подразделе 1.2:

Проекции i_1х и i_1у представляют собой синусоидальную и косинусоидальную функции соответственно.

Приравнивая вещественные и мнимые части этих выражений, получим формулы преобразования двухфазных величин в трехфазные в неподвижной системе координат:

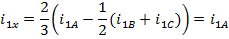
Упрощение первого из этих выражений достигнуто добавлением и вычитанием в квадратных скобках слагаемого (1 / 2) i₁_A и учетом того, что в симметричной трехфазной системе выполняется равенство i₁_A + i₁_B + i₁_C = 0. Можно записать и, воспользовавшись правилом перехода от показательной формы комплексного числа к тригонометрической, получить для вектора тока статора:

откуда получается правило расчета проекций пространственного вектора в виде:

При преобразовании проекций на оси вращающейся системы координат в двухфазную систему получим:

Из равенства i₁_A + i₁_B + i₁_C = 0 мгновенное значение тока фазы А определяется как

i₁_A =-(i₁_B + i₁_C). Поскольку i₁_A = i_1х можно записать:

откуда получаются выражения для определения мгновенных значений тока в трехфазной системе, выраженные через токи в двухфазной системе:

Для вычислений надо располагать мгновенными значениями угла θс. Он рассчитывается следующим образом:

где 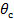- угол между общей системы координат α - и системы координат статора x – y.

На основе выше сказанного построены модели преобразователей систем координат, реализованные по уравнениям, в MatLab Simulink.

1) Преобразование из α-β в x-y и в АВС.

В качестве исходных данных для построения схемы используем следующие уравнения:

На рисунке 2.5. представлена структурная схема преобразования координат по данным уравнениям. На вход модели поданы проекции пространственного вектора тока на вращающиеся оси () и текущее время. На выходе модели получены токи в неподвижной системе координат (), а также трехфазные токи (). На вход модели преобразования координат подаются следующие значения . На рис. 2.7 представлены результаты моделирования преобразователя – трехфазные токи с частотой 50 Гц. На рис. 2.8 представлены промежуточные результаты моделирования – двухфазные токи в статорной системе координат.

Аналогичная модель строится и для преобразования переменных от неподвижной системы координат к вращающейся. Следует отметить, что в этом случае на вход модели подаются синусоидальные функции времени, а на выходе получаются постоянные величины.

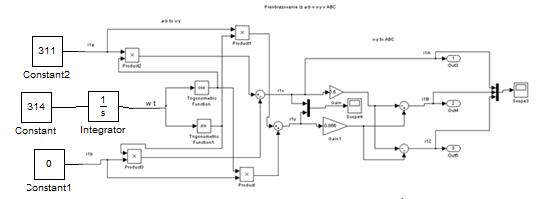
Рис.2.5 Структурная схема преобразования α-β в x-y и в АВС

Так как данная схема (см. рис. 2.5) может быть частью большой системы, то можно свернуть ее в блоки. Для этого нужно выделить необходимое количество элементов, которое нужно объединить и, используя контекстное меню, выбрать пункт «Create Subsystem». Тогда схема упроститься, и будет иметь вид, представленный на рис.2.6.

Рис.2.6 Упрощенная схема преобразования координат

Рис.2.7 трехфазные токи I_A₁I_B1I_C₁

Рис.2.8 Двухфазные токи в неподвижной системе координат I_xI_y

2) Преобразование из АВС в x-y и в α-β.

В качестве исходных данных для построения схемы используем следующие уравнения:

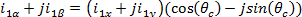
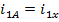
На рисунке 2.9 представлена структурная схема преобразования координат по данным уравнениям. В этом случае на вход модели подаются синусоидальные функции времени, которые заимствованы из преобразования α-β в x-y и в АВС, а на выходе получаются постоянные величины . Результат преобразования представлен на рис.2.10.

Рис.2.9 Структурная схема преобразования АВС в x-y и в α-β

Рис.2.10 Токи α-β

3) Преобразования из ABC –xy – dq

Используя следующие математические выражения можно осуществить преобразования координат, а также построить структурные схемы на их основе в MatLab Simulink:

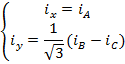
Где

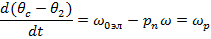
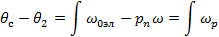
Где θ₂ - угол между осью вещественных d роторной системы и неподвижной осью х статорной системы координат; θ_с - угол между осью α и неподвижной осью х статорной системы координат.

4) Преобразования от dq к αβ

Можно записать

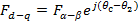
и, воспользовавшись правилом перехода от показательной формы комплексного числа к тригонометрической, получить:

Для :

Для :

откуда получается правило расчета проекций пространственного вектора в виде:

Для :

Для :

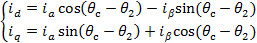
Преобразования «ABC –xy – dq» и «dq к αβ» представлены только в виде математических преобразований, так как в данной работе они не участвуют и при необходимости могут быть воспроизведены в структурные схемы по аналогии с преобразованиями «α-β в x-y и в АВС».

Воспользуйтесь поиском по сайту: