Приложение Б. Интеграл ошибок. II

Приложение А. Интеграл ошибок. I

 

Вероятность, выраженная в процентах, P (в пределах ts) = , как функция t.

Вероятность того, что результат измерения окажется вне этого же интервала, можно найти с помощью вычитания: P (вне ts) = 100 % — P (в пределах ts).

 

t	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.06	0.07	0.09
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.0 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.5 4.0 4.5 5.0	0.00 7.97 15.85 23.58 31.08 38.29 45.15 51.61 57.63 63.19 68.27 72.87 76.99 80.64 83.85 86.64 89.04 91.09 92.81 94.26 95.45 96.43 97.22 97.86 98.36 98.76 99.07 99.31 99.49 99.63 99.73 99.95 99.994 99.9993 99.99994	0.80 8.76 16.63 24.34 31.82 38.99 45.81 52.23 58.21 63.72 68.75 73.30 77.37 80.98 84.15 86.90 89.26 91.27 92.97 94.39 95.56 96.51 97.29 97.91 98.40 98.79 99.09 99.33 99.50 99.64 – – – – –	1.60 9.55 17.41 25.10 32.55 39.69 46.47 52.85 58.78 64.24 69.23 73.73 77.75 81.32 84.44 87.15 89.48 91.46 93.12 94.51 95.66 96.60 97.36 97.97 98.45 98.83 99.12 99.35 99.52 99.65 – – – – –	2.39 10.34 18.19 25.86 33.28 40.39 47.13 53.46 59.35 64.76 69.70 74.15 78.13 81.65 84.73 87.40 89.69 91.64 93.28 94.64 95.76 96.68 97.43 98.02 98.49 98.86 99.15 99.37 99.53 99.66 – – – – –	3.19 11.13 18.97 26.61 34.01 41.08 47.78 54.07 59.91 65.28 70.17 74.57 78.50 81.98 85.01 87.64 89.90 91.81 93.42 94.76 95.86 96.76 97.49 98.07 98.53 98.89 99.17 99.39 99.55 99.67 – – – – –	3.99 11.92 19.74 27.37 34.73 41.77 48.43 54.67 60.47 65.79 70.63 74.99 78.87 82.30 85.29 87.89 90.11 91.99 93.57 94.88 95.96 96.84 97.56 98.12 98.57 98.92 99.20 99.40 99.56 99.68 – – – – –	4.78 12.71 20.51 28.12 35.45 42.45 49.07 55.27 61.02 66.29 71.09 75.40 79.23 82.62 85.57 88.12 90.31 92.16 93.71 95.00 96.06 96.92 97.62 98.17 98.61 98.95 99.22 99.42 99.58 99.69 – – – – –	5.58 13.50 21.28 28.86 36.16 43.13 49.71 55.87 61.57 66.80 71.54 75.80 79.59 82.93 85.84 88.36 90.51 92.33 93.85 95.12 96.15 97.00 97.68 98.22 98.65 98.98 99.24 99.44 99.59 99.70 – – – – –	6.38 14.28 22.05 29.61 36.88 43.81 50.35 56.46 62.11 67.29 71.99 76.20 79.95 83.24 86.11 88.59 90.70 92.49 93.99 95.23 96.25 97.07 97.74 98.27 98.69 99.01 99.26 99.46 99.60 99.71 – – – – –	7.17 15.07 22.82 30.35 37.59 44.48 50.98 57.05 62.65 67.78 72.43 76.60 80.29 83.55 86.38 88.82 90.90 92.65 94.12 95.34 96.34 97.15 97.80 98.32 98.72 99.04 99.29 99.47 99.61 99.72 – – – – –

 

Приложение Б. Интеграл ошибок. II

В некоторых расчетах удобной формой интеграла ошибок является следующая:

Вероятность Р (а £ х ³ b) того, что результат измерения окажется в любом интервале а £ х ³ b, можно найти по значению Q (t) с помощью одного вычитания или сложения. Например,

Р (X + s £ х ³ X + 2s) = Q (2) - Q (1)
Р (X - 2s £ х ³ X + s) = Q (2) + Q (1)
Вероятность того, что результат измерения окажется больше, чем любое X + t s, равна 0.5 ‑ Q (t). Например, Р (х ³ X + s) = 50% - Q (1)

 

t	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.06	0.07	0.09
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1^ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.5 4.0 4.5 5.0	0.00 3.98 7.93 11.79 15.54 19.15 22.57 25.80 28.81 31.59 34.13 36.43 38.49 40.32 41.92 43.32 44.52 45.54 46.41 47.13 47.72 48.21 48.61 48.93 49.18 49.38 49.53 49.65 49.74 49.81 49.87 49.98 49.997 49.9997 49.99997	0.40 4.38 8.32 12.17 15.91 19.50 22.91 26.11 29.10 31.86 34.38 36.65 38.69 40.49 42.07 43.45 44.63 45.64 46.49 47.19 47.78 48.26 48.64 48.96 49.20 49.40 49.55 49.66 49.75 49.82 – – – – –	0.80 4.78 8.71 12.55 16.28 19.85 23.24 26.42 29.39 32.12 34.61 36.86 38.88 40.66 42.22 43.57 44.74 45.73 46.56 47.26 47.83 48.30 48.68 48.98 49.22 49.41 49.56 49.67 49.76 49.82 – – – – –	1.20 5.17 9.10 12.93 16.64 20.19 23.57 26.73 29.67 32.38 34.85 37.08 39.07 40.82 42.36 43.70 44.84 45.82 46.64 47.32 47.88 48.34 48.71 49.01 49.25 49.43 49.57 49.68 49.77 49.83 – – – – –	1.60 5.57 9.48 13.31 17.00 20.54 23.89 27.04 29.95 32.64 35.08 37.29 39.25 40.99 42.51 43.82 44.95 45.91 46.71 47.38 47.93 48.38 48.75 49.04 49.27 49.45 49.59 49.69 49.77 49.84 – – – – –	1.99 5.% 9.87 13.68 17.36 20.88 24.22 27.34 30.23 32.89 35.31 37.49 39.44 41.15 42.65 43.94 45.05 45.99 46.78 47.44 47.98 48.42 48.78 49.06 49.29 49.46 49.60 49.70 49.78 49.84 – – – – –	2.39 6.36 10.26 14.06 17.72 21.23 24.54 27.64 30.51 33.15 35.54 37.70 39.62 41.31 42.79 44.06 45.15 46.08 46.86 47.50 48.03 48.46 48.81 49.09 49.31 49.48 49.61 49.71 49.79 49.85 – – – – –	2.79 6.75 10.64 14.43 18.08 21.57 24.86 27.94 30.78 33.40 35.77 37.90 39.80 41.47 42.92 44.18 45.25 46.16 46.93 47.56 48.08 48.50 48.84 49.11 49.32 49.49 49.62 49.72 49.79 49.85 – – – – –	3.19 7.14 11.03 14.80 18.44 21.90 25.17 28.23 31.06 33.65 35.99 38.10 39.97 41.62 43.06 44.29 45.35 46.25 46.99 47.61 48.12 48.54 48.87 49.13 49.34 49.51 49.63 49.73 49.80 49.86 – – – – –	3.59 7.5а 11.41 15.17 18.79 22.24 25.49 28.52 31.за 33.8» 36.21 38.30> 40. IS 41.77 43.19 44.41 45.45 46.3а 47.06- 47.67 48.17 48.57 48.90 49.16 49.36 49.52 49.64 49.74 49.81 49.86 – – – – –

Приложение В. Вероятности коэффициентов корреляции

 

Степень, с которой N точек (x_i, y_i) аппроксимируются прямой линией, определяется коэффициентом линейной корреляции:

,

который всегда лежит в интервале –1 £ r ³ 1. Значения r, близкие к ±1, означают высокую степень линейной корреляции; значения, близкие к 0, указывают на небольшую корреляцию или на ее отсутствие. Количественная мера аппроксимации может быть получена с помощью табл. В. Для любого определенного r ₀ Р_N (| r | ³ | r ₀|) есть вероятность того, что результаты N измерений двух некоррелированных переменных будут иметь коэффициент корреляции г, не меньший чем r ₀. Таким образом, если мы получим коэффициент r ₀, для которого вероятность Р_N (| r | ³ | r ₀|) мала, то невероятно, чтобы наши переменные были некоррелированными, т. е. корреляция существует. В частности, если Р_N (| r | ³ | r ₀|) £ 5%, корреляция называется значимой, если эта вероятность меньше 1%, то корреляция называется высокозначимой. Например, вероятность того, что результаты 20 измерений (N = 20) двух некоррелированных переменных дадут | r | ³ 0.5, определяется таблицей в 2.5%- Таким образом, если бы результаты 20 измерений дали r = 0.5, то у нас было бы значимое доказательство линейной корреляции между двумя переменными. Значения, приведенные в табл. В, были вычислены по формуле

Р_N (| r | ³ | r ₀|) =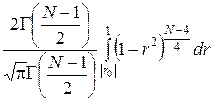

Таблица В. Выраженная в процентах вероятность Р_N (| r | ³ | r ₀|) того, что результаты N измерений двух некоррелированных переменных дадут коэффициент корреляции | r | ³ | r ₀|, как функция N и r ₀. (Прочерки указывают на вероятности, которые меньше 0.05%.)

r 0
N		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
				8.0 6.0 4.5	9.0 8.1 4.8 2.9 1.7 1.1 0.6	9.8 8.2 6.9 5.8 4.9 4.1 3.5 2.9 2.5 1.1 0.5 0.2 0.1 ---	8.8 6.7 5.1 3.9 3.0 2.3 1.8 1.4 1.1 0.8 0.7 0.5 0.2 --- --- --- ---	8.0 5.3 3.6 2.4 1.6 1.1 0.8 0.5 0.4 0.3 0.2 0.1 0.1 0.1 --- --- --- --- ---	5.6 3.1 1.7 1.0 0.5 0.3 0.2 0.1 0.1 --- --- --- --- --- --- --- --- --- --- ---	3.7 1.4 0.6 0.2 0.1 --- --- --- --- --- --- --- --- --- --- --- --- --- --- --- ---

 

		0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45
					9.7 7.5 5.9 4.6	8.0 5.4 3.7 2.5 1.7 1.2	3.4 2.0 1.2 0.7 0.4 0.2	1.3 0.6 0.3 0.1 0.1 ---	0.4 0.2 0.1 --- --- ---	0.1 --- --- --- --- ---

 

Приложение Г. Вероятности для c ²

 

Если результаты серии измерений распределены по k бинам, где k = 1,... n, то через O_k мы обозначим число наблюдений, попавших в бин k. Ожидаемое число (полученное на основе некоторого предположенного или ожидаемого распределения) результатов в бине k обозначается E_k. Степень, с которой результаты наблюдений аппроксимируются предполагаемым распределением, характеризуется приведенным значением c ², определяемым как c² = / d, где d есть число степеней свободы, равное d = n – c, а с — число связей. Ожидаемое среднее значение c ² равно 1. Если c ² >> 1, то результаты наблюдений не согласуются с предполагаемым распределением; если c ² £ 1, то согласие удовлетворительное. Этот критерий становится количественным благодаря вероятностям, приведенным в табл. Г. Пусть c_о обозначает значение c ² фактически полученное в эксперименте с d степенями свободы. Число P_d (c ² ³ c_о ²) есть вероятность получения значения c ² не меньшего, чем полученное c_о ², если результаты измерений действительно распределены в соответствии с предположенным законом. Таким образом, если P_d (c ² ³ c_о ²) велика, то полученное и ожидаемое распределения согласуются; если эта вероятность мала, то они, по-видимому, различаются. В частности, если P_d (c ² ³ c_о ²) меньше 5%, мы говорим, что расхождение значимо, и отвергаем предположенное распределение на 5%-ном уровне. Если эта вероятность меньше 1 %, расхождение называется высокозначимым и мы отвергаем предположенное распределение на 1%-ном уровне. Например, предположим, что мы получили для приведенного значения c ² 2.6 (т. е. c_о ² = 2.6) в эксперименте с шестью степенями свободы (d = 6). В соответствии с табл. Г вероятность получения %2 ^ 2,6 составляет 1,6%, если результаты измерений распределены в соответствии с предположенным законом. Таким образом, на 5% -ном уровне (но не на 1%-ном) мы отвергли бы предположенное распределение. Значения, представленные в табл. Г, были рассчитаны по формуле

 

P_d (c ² ³ c_о ²) =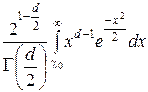

 

Таблица Г. Выраженная в процентах вероятность P_d (c ² ³ c_о ²) получения значения c ² ³ c_о ² в эксперименте с d степенями свободы как функция d и c_о ². (Прочерки указывают на значения вероятности, которые меньше 0.05%.)

	cо 2
d		0.5		1.5		2.5		3.5		4.5		5.5
					9.2 7.5	8.2 5.8 4.0 2.9	8.3 5.0 2.9 1.7 1.0	6.1 3.0 1.5 0.7 0.4	4.6 1.8 0.7 0.3 0.1	3.4 1.1 0.4 0.1 ---	2.5 0.7 0.2 0.1 ---	1.9 0.4 0.1 --- ---	1.4 0.2 --- --- ---	0.5 --- --- --- ---	0.2 --- --- --- ---

 

	cо 2
d	0.2	0.4	0.6	0.8	1.0	1.2	1.4	1.6	1.8	2.0	2.2	2.4	2.6	2.8	3.0
							9.2 8.5 7.8 7.2	9.1 8.4 7.7 7.1 6.5 6.0 5.5 5.1 4.7 4.3 3.7 3.2 2.7 2.3 2.0	9.5 8.2 7.2 6.3 5.5 4.8 4.2 3.7 3.3 2.9 2.5 2.2 2.0 1.7 1.5 1.2 0.9 0.7 0.6 0.5	7.5 6.2 5.1 4.2 3.5 2.9 2.4 2.0 1.7 1.4 1.2 1.0 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.1	8.6 5.1 4.0 3.1 2.4 1.9 1.5 1.2 0.9 0.7 0.6 0.5 0.4 0.3 0.2 0.2 0.1 0.1 0.1 — — —	9.1 6.6 3.5 2.5 1.9 1.4 1.0 0.8 0.6 0.4 0.3 0.2 0.2 0.1 0.1 0.1 0.1 — — — — — —	7.4 5.0 3 4 2.3 1.6 1.1 0.8 0.5 0.4 0.3 0.2 0.1 0.1 0.1 — — — — — — — — — —	9.4 6.1 3.8 9.4 1.6 1.0 0.7 0.4 0.3 0.2 0.1 0.1 0.1 — — — — — — — — — — — —	8.3 5.0 2.9 1 7 1.0 0.6 0.4 0.2 0.1 0.1 0.1 — — — — — — — — — — — — — —

 

Поделиться:

Воспользуйтесь поиском по сайту: