Главная | Обратная связь | Поможем написать вашу работу!

Таблицы 2, 3. Результаты измерений и расчётов

Стр 1 из 2Следующая ⇒

ПРИЛОЖЕНИЕ №1

К ВИРТУАЛЬНОМУ ПРАКТИКУМУ ПО ФИЗИКЕ

ДЛЯ ВУЗОВ

ЛАБОРАТОРНЫЕ РАБОТЫ

по курсу физики

С компьютерными моделями

для студентов всех специальностей

всех форм обучения

МОСКВА - 2002

Б.К.Лаптенков

Приложение №1 к Виртуальному практикуму по физике для ВУЗов. Лабораторные работы по курсу физики с компьютерными моделями.

Учебное пособие для студентов высших технических учебных заведений дневной, вечерней и заочной (дистанционной) форм обучения. -М.:2002.-64 с.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ....................................................................................................................................4

ЛАБОРАТОРНАЯ РАБОТА № 1.6...................................………………………….................5

ЛАБОРАТОРНАЯ РАБОТА № 1.7........................………………………................................9

ЛАБОРАТОРНАЯ РАБОТА № 1.8........................………………………...............................14

ЛАБОРАТОРНАЯ РАБОТА № 1.9........................………………………...............................17

ЛАБОРАТОРНАЯ РАБОТА № 2.10...................................………………………..................23

ЛАБОРАТОРНАЯ РАБОТА № 2.11..........................................………………………...........29

ЛАБОРАТОРНАЯ РАБОТА № 2.12............................……………………….........................32

ЛАБОРАТОРНАЯ РАБОТА № 2.13..................................………………………...................35

ЛАБОРАТОРНАЯ РАБОТА № 2.14.....................................………………………................39

ЛАБОРАТОРНАЯ РАБОТА № 2.15..................................………………………...................44

ЛАБОРАТОРНАЯ РАБОТА № 2.16..............................……………………….............…......48

ЛАБОРАТОРНАЯ РАБОТА № 2.17......................…………….…………..............................52

ЛАБОРАТОРНАЯ РАБОТА № 3.5......................................……………….………................59

ЛАБОРАТОРНАЯ РАБОТА № 4.5.................................…………………….….....................63

ЛАБОРАТОРНАЯ РАБОТА № 4.6..........................................................................................67

ЛАБОРАТОРНАЯ РАБОТА № 4.7..........................................................................................73

ВВЕДЕНИЕ

Методическое пособие: «Приложение №1 к Виртуальному практикуму по физике для ВУЗов» разработано кандидатом физико-математических наук, доцентом кафедры общей физики Волжского филиала МАДИ (ГТУ), доцентом кафедры общей физики ЧувГУ Лаптенковым Б.К. Пособие подготовлено на базе обучающей программы ООО «ФИЗИКОН» «Открытая Физика 1.1» и является дополнением к комплекту лабораторных работ, вошедших в состав «Виртуального практикума по физике для ВУЗов» и разработанных профессором МГТУГА Тихомировым Ю.В. В стилевом оформлении и методическом подходе описание работ Приложения полностью соответствует описанию работ Виртуального практикума.

ЛАБОРАТОРНАЯ РАБОТА № 1.6

ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ

Ознакомьтесь с теорией в конспекте и в учебниках 1. Трофимова Т.И. Курс физики. Гл.3, §§12,13. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл.3, §§3.1-3.4. Выберите «Механика» и «Движение тела по наклонной плоскости». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите основные сведения в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.

ЦЕЛЬ РАБОТЫ:

· Знакомство с применением физических моделей - консервативная и диссипативная механическая система.

· Экспериментальная проверка закона сохранения механической энергии в консервативных и диссипативных системах.

КРАТКАЯ ТЕОРИЯ:

РАБОТУ ПОСТОЯННОЙ СИЛЫ 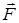на перемещение её точки приложения измеряют произведением

, (1)

где a-угол между направлением силы и перемещения. Если на тело действует несколько сил, каждая из которых совершает над ним работу, то вся произведённая работа равна алгебраической сумме работ отдельных сил:

(2)

ЭНЕРГИЯ-универсальная мера различных форм движения и взаимодействия материи. Часть энергии тела, соответствующую механическим формам движения материи называют механической энергией. Её принято делить на кинетическую и потенциальную.

В случае движения материальной точки или поступательного движения твёрдого тела

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ равна . (3)

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ W_п- часть механической энергии, обусловленная взаимным расположением тел или частей тела и их взаимодействием друг с другом.

ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ ТЕЛ равна арифметической сумме кинетических и потенциальных энергий всех тел, входящих в данную систему: W_полн = 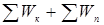. (4)

КОНСЕРВАТИВНЫМИ называются силы, работа которых при перемещении

тела из одного состояния в другое не зависит от того, по какой траектории произошло это перемещение.

Если работа по перемещению тела зависит от траектории перемещения из одной точки в другую, то такая сила называется ДИССИПАТИВНОЙ.

ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ: Изменение кинетической энергии равно работе всех сил, действующих на это тело.

ТЕОРЕМА О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ: Работа консервативных сил равна изменению потенциальной энергии системы, взятому с противоположным знаком.

А_конс = - (W_п2 - W_п1). (5)

ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется.

W _полн = const. (6)

Если на тело в процессе его перехода из одного состояния в другое кроме консервативных сил (сил тяготения и упругости) действуют другие силы, то изменение полной механической энергии равно работе этих сил:

W_полн2 - W_полн1= . (7)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Внимательно рассмотрите окно опыта. Найдите все регуляторы и другие основные элементы. Зарисуйте в свой конспект схему опыта.

После нажатия мышью кнопки «Выбор» установите с помощью движков регуляторов значения массы тела m, угла наклона плоскости a, внешней силы F_вн _, коэффициента трения m и ускорения а, указанных в табл.1 для вашей бригады.

Потренируйтесь в синхронном включении секундомера и снятия метки «тело закреплено» одиночным щелчком курсора мыши на кнопке в правом нижнем углу окна опыта

Одновременно включите секундомер и снимите метку «тело закреплено». Выключите секундомер в момент остановки тела в конце наклонной плоскости.

Проделайте этот опыт 10 раз и результаты измерения времени соскальзывания тела с наклонной плоскости запишите в табл. 2.

ТАБЛИЦА 1. Исходные параметры опыта

№ бриг.
m, кг	2,0	2,2	2,4	2,6	2,8	3,0	2,9	2,7
m	0,10	0,14	0,18	0,22	0,26	0,30	0,34	0,38
a,град
_F_вн, Н	-4	-3	-2	-1
а,м/с²

ТАБЛИЦА 2. Результаты измерений и расчётов

№ изм.

Сред. знач.

t, с

v, м/с

S, м

W_к, Дж

W_п, Дж

A_тр,Дж

A_вн, Дж

W_полн, Дж

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:

Вычислите по формулам:

а) vt - скорость тела в конце наклонной плоскости;

б) - длину наклонной плоскости;

в) 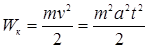- кинетическую энергию тела, в конце наклонной плоскости;

г) 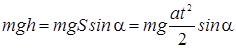- потенциальную энергию тела в верхней точке наклонной плоскости;

д) - работу силы трения на участке спуска;

е) - работу внешней силы на участке спуска

и запишите эти значения в соответствующие строки табл. 2.

Вычислите средние значения этих параметров и запишите их в столбец «средние значения» табл.2.

По формуле (7) проверьте выполнение закона сохранения механической энергии при движении тела по наклонной плоскости, рассчитайте погрешности и сделайте выводы по результатам проведённых опытов.

Вопросы и задания для самоконтроля

1. В чём заключается закон сохранения механической энергии?

2. Для каких систем выполняется закон сохранения механической энергии?

3. В чём состоит различие между понятиями энергии и работы?

4. Чем обусловлено изменение потенциальной энергии?

5. Чем обусловлено изменение кинетической энергии?

6. Необходимо ли выполнение условия замкнутости механической системы тел для выполнения закона сохранения механической энергии?

7. Какие силы называются консервативными?

8. Какие силы называются диссипативными?

9. Тело медленно втаскивают в гору. Зависят ли от формы профиля горы: а) работа силы тяжести; б) работа силы трения? Начальная и конечная точки перемещения тела фиксированы.

10. Тело соскальзывает с вершины наклонной плоскости без начальной скорости. Зависит ли работа силы трения на всём пути движения тела до остановки на горизонтальном участке: а) от угла наклона плоскости; б) от коэффициента трения?

11. По наклонной плоскости с одной и той же высоты соскальзывают два тела: одно массой m, другое массой 2m. Какое из тел пройдёт до остановки по горизонтальному участку путь больший и во сколько раз? Коэффициенты трения для обоих тел одинаковы.

12. Санки массой m скатились с горы высотой Н и остановились на горизонтальном участке. Какую работу необходимо совершить для того, чтобы поднять их на гору по линии скатывания.

13. С одинаковой начальной скоростью тело проходит: а) впадину; б) горку, имеющие одинаковые дуги траекторий и одинаковые коэффициенты трения. Сравните скорости тела в конце пути в обоих случаях.

ЛАБОРАТОРНАЯ РАБОТА № 1.7

ИЗУЧЕНИЕ ЗАКОНОВ ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

Ознакомьтесь с теорией в конспекте и в учебниках 1. Трофимова Т.И. Курс физики. Гл.6, §§28,29,30. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл.3, §§3.5. Выберите «Механика» и «Течение идеальной жидкости». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите основные сведения в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.

ЦЕЛЬ РАБОТЫ:

· Знакомство с компьютерной моделью течения идеальной жидкости.

· Экспериментальная проверка уравнений неразрывности и Бернулли.

· Экспериментальное определение расхода жидкости.

КРАТКАЯ ТЕОРИЯ:

ИДЕАЛЬНОЙ ЖИДКОСТЬЮ называется жидкость, в которой отсутствует внутреннее трение.

ЛИНИЕЙ ТОКА называется мысленно проведённая в потоке линия, касательная к которой в любой её точке совпадает по направлению с вектором скорости жидкости в этой точке.

ТРУБКОЙ ТОКА называется поверхность, образованная линиями тока, которые проведены через все точки замкнутого контура.

ДАВЛЕНИЕМ р жидкости называется физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади

. (1)

Если жидкость несжимаема, то её плотность не зависит от давления. Тогда при поперечном сечении S столба жидкости на глубине h при плотности r вес будет равен P = rgSh, а давление на нижнее основание

, (2)

которое называется гидростатическим давлением.

УРАВНЕНИЕ НЕРАЗРЫВНОСТИ для несжимаемой жидкости имеет вид:

Sv = const. (3)

УРАВНЕНИЕ БЕРНУЛЛИ:

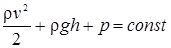, (4)

где р называется статическим давлением, - динамическим давлением.

Для горизонтальной трубки тока (h₁=h₂) выражение (4) принимает вид

(5) и называется полным давлением.

Из уравнения (5) следует, что давление и скорость течения жидкости в двух точках 1и 2 на одной и той же линии тока связаны соотношением:

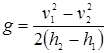или (6)

РАСХОДОМ ЖИДКОСТИ называется объём жидкости Q, протекающий за 1 с через поперечное сечение трубы

Q = vS. (7)

Пусть S₁ и S₂ – площади поперечного сечения широкого и узкого участков трубы, а р₁ и р₂ – статические давления в этих сечениях трубы, измеряемые с помощью манометрических трубок. Тогда уравнение Бернулли (5) можно записать в виде

(8)

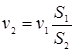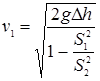Так как жидкость несжимаема, то rv₁S₁=rv₂S₂, . С другой стороны: , и = . Откуда получим: и Q = . (9)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Внимательно рассмотрите рисунок опыта и зарисуйте необходимое в свой конспект лабораторной работы.

1. Установите с помощью мыши одинаковое значение диаметров трубы d₁= d₂= d₃ на всех трёх её участках, равное величине D₁, указанное в табл.1 для вашей бригады.

2. С помощью миллиметровой линейки измерьте всю длину трубы от левого края окна опыта до правого L_экс и её диаметр D_экс

3. Определите «модельную» длину трубы L_m по формуле и запишите эти значения в табл. 2.

4. Нажатием кнопки;в верхней части окна опыта остановите течение жидкости.

5. Зафиксируйте своё внимание на пунктирной линии в жидкости (5 вертикальных светлых точек в трубе), находящейся на входе в трубу. Нажатием кнопки8 возобновите течение жидкости по трубе и одновременно включите секундомер. Не выпуская из внимания выделенную линию и сопровождая визуально её течение по трубе, выключите секундомер в момент прохождения ей выходного сечения трубы. Запишите это время в таблицу 2.

6. Проделайте этот опыт 10 раз и каждое значение t_i запишите в таблицу 2.

7. Запишите в табл. 2 значения H₁ = h₁ =h₂= h₃.

8. С помощью курсора мыши установите второе, одинаковое для всех трёх секций трубы, значение диаметра D₂, указанное в таблице 1 для вашей бригады, и повторите измерения по п.п. 1-7.

ТАБЛИЦА 1. Значения диаметров трубы

Номер бригады	D1 мм	D2 мм	Номер бригады	D1 мм	D2 мм

ТАБЛИЦА 2. Результаты измерений

Номер измерения	D₁=____ H₁=____	D₂=____ H₂= ___
t_i	v_i	g_i	t_i	v_i	g_i


…

Средние значения

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:

1.По формуле определите скорость течения жидкости в каждом опыте и её среднее значение и .

2. По формуле определите экспериментальное значение ускорения свободного падения и сравните его с теоретическим значением.

3. По формуле проверьте выполнение в вашем опыте уравнения неразрывности.

4. По формуле (9) рассчитайте объём жидкости, протекающей через сечение трубы за 1 с.

5. Определите погрешность проведённых измерений.

Вопросы и задания для самоконтроля

1. Каков физический смысл уравнения неразрывности для несжимаемой жидкости и как его вывести?

2. Выведите уравнение Бернулли.

3. Как в потоке жидкости можно измерить статическое, динамическое и полное давление?

4. Сформулируйте и объясните законы Архимеда и Паскаля.

5. Какое течение жидкости называется ламинарным и турбулентным?

6. Каким критерием определяется переход режима течения жидкости от ламинарного к турбулентному?

7. Какое явление называется вязкостью жидкости?

ЛАБОРАТОРНАЯ РАБОТА № 1.8

ИЗУЧЕНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ СТРУНЫ

(«Механические колебания и волны», «Нормальные моды струны»)

ЦЕЛЬ РАБОТЫ:

· Изучение колебаний в системах с распределёнными параметрами на примере поперечных стоячих волн в упругой горизонтальной струне.

· Наблюдение картины распределения амплитуд колебаний точек струны при образовании стоячих волн.

· Количественная проверка формулы скорости распространения колебаний вдоль струны.

КРАТКАЯ ТЕОРИЯ:

СТОЯЧИЕ ВОЛНЫ – это особый случай интерференции, возникающий при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами:

x₁ = A cos (wt – kx), x₂ = A cos (wt + kx) (1)

Сложив эти уравнения и учитывая, что k = 2p/l, получим уравнение стоячей волны:

x = x₁ + x₂ = 2А cos kx cos wt = 2A cos (2px/l) cos wt. (2)

Из уравнения (2) следует, что в каждой точке этой волны происходят колебания с одной и той же частотой w и амплитудой 2A cos (2px/l), зависящей от координаты х рассматриваемой точки.

В точках среды, где 2px/l =± mp (m = 0,1,2,…), амплитуда колебаний достигает максимального значения, равного 2А. В точках среды, где 2px/l = ±(m +1/2)p, амплитуда колебаний обращается в нуль.

Точки, в которых амплитуда максимальна, называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.

В гибкой однородной струне, натянутой между двумя точками и выведенной из положения равновесия, могут установиться стоячие волны. При этом на длине струны L всегда должно укладываться целое число стоячих волн. При этом струна делится неподвижными точками – узлами – на несколько равных отрезков, длина которых равна половине длины бегущей волны. Следовательно, можно записать

L = n (l/2), (3)

где n – целое число, определяющее количество полуволн, уложившихся на всей длине струны L.

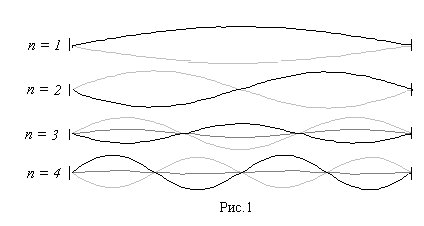Так, как длина волны l связана со скоростью распространения волны v и частотой n соотношением v = ln, то, учитывая (3), имеем n= . (4)

Струна, следовательно, может колебаться не с одной частотой, а с целым спектром частот, соответствующим собственным (нормальным) колебаниям струны. В общем случае любые сложные колебания в струне можно представить как суперпозиция нескольких собственных колебаний, отличающихся не только своими частотами, но и своими амплитудами для отдельных точек струны. Распределение амплитуд отдельных точек волны при собственных колебаниях для различных значений n имеет вид, изображённый на рис.1.

Опыт показывает, что скорость распространения импульса деформаций (колебаний) вдоль струны определяется силой натяжения струны F и линейной плотностью m материала струны:

. (5)

Тогда с учётом формулы (5) формула (4) примет вид:

. (6)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

1. Установите с помощью движков регуляторов постоянные значения линейной плотности материала и силы натяжения струны, указанных в таблице 1 для вашей бригады.

2. Установите начальную частоту колебания струны f = 1,0 Гц и, постепенно увеличивая её значение, получите устойчивые колебания струны при n = 1 (см распределение амплитуд точек струны при n = 1).

3. Аналогичным образом получите стоячие волны соответствующие различным значениям n и заполните табл.2.

4. Установите второе значение линейной плотности материала струны из табл.1 для вашей бригады и проделайте измерения п.2 и 3 ещё раз и заполните табл.3.

Таблица 1.

№ бригады
Т, Н	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8
m, г/м	5,1 9,1	5,2 9,2	5,3 9,3	5,4 9,4	5,5 9,5	5,6 9,6	5,7 9,7	5,8 9,8

Таблицы 2, 3. Результаты измерений и расчётов

n_i
n_i

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:

1. Результаты измерений представьте в виде двух графиков, откладывая по оси абсцисс значения , а по оси ординат – соответствующие им значения .

2. По тангенсу угла наклона к оси абсцисс каждого графика определите, используя формулу , значения линейной плотности материала струны и сравните его значение с установочным.

3. Оцените погрешность измерений и сделайте выводы по графикам и ответу.

Вопросы и задания для самоконтроля

1. Что такое волна?

2. Какая волна называется продольной?

3. Какая волна называется поперечной?

4. Что такое волновой фронт и волновая поверхность?

5. Что называется длиной волны, волновым числом?

6. Какая волна является: а) бегущей; б) стоячей; в) плоской;

г) сферической?

7. При каких условиях возникают стоячие волны?

8. Запишите уравнение стоячей волны.

9. Запишите волновое уравнение.

10. Чем стоячая волна отличается от бегущей?

11. Что такое пучность и узел стоячей волны?

12. Чему равно расстояние между двумя ближайшими пучностями стоячей волны?

13. Запищите формулы определения координат пучностей и узлов стоячей волны.

14. Объясните механизм образования стоячих волн при отражении бегущей волны от границы раздела двух сред различной плотности.

15. От чего зависит скорость распространения упругой волны в струне?

16. Что такое основная частота струны?

17. Что такое гармоники основной частоты?

18. Запишите соотношение между частотой и волновым числом нормальных мод струны.

19. Какие волны называют диспергирующими?

20. Что такое Фурье-анализ?

ЛИТЕРАТУРА

1. Трофимова Т.И. Курс физики. М.: Высшая школа, 2001, Гл.19, §157.

2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2000, Гл.29, §§29.6

ЛАБОРАТОРНАЯ РАБОТА № 1.9

ИЗУЧЕНИЕ ОСНОВНЫХ СВОЙСТВ МЕХАНИЧЕСКИХ ВОЛН

(«Механические колебания и волны», «Механические волны»)

ЦЕЛЬ РАБОТЫ:

· Определение фазовой скорости распространения поперечных волн на натянутом жгуте.

· Проверка формулы фазовой скорости распространения волн на поверхности жидкости.

КРАТКАЯ ТЕОРИЯ:

Процесс распространения колебаний в сплошной среде называется механическим ВОЛНОВЫМ ПРОЦЕССОМ ИЛИ ВОЛНОЙ.

Основное свойство всех волн состоит в том, что в волне происходит перенос энергии без переноса вещества.

Каждый тип механических волн может быть возбужден в определенном веществе или среде. При распространении волны частицы среды в зависимости от природы волны испытывают смещения различного рода.

Если частицы среды испытывают смещения в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Примером волны такого рода может служить волна в натянутой струне.

Если смещения частиц среды происходят в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне или звуковые волны в газе являются примерами продольных волн.

Волны на поверхности воды имеют как поперечную, так и продольную компоненты.

В каждом типе бегущих волн возмущение распространяется через среду с определенной скоростью, зависящей от типа волны и свойств среды.

Скорость поперечных волн в струне зависит от ее погонной массы m (масса единицы длины) и силы натяжения T:

Скорость распространения продольных волн зависит от модуля сжатия В и плотности среды:

В случае твердого стержня модуль сжатия равен модулю Юнга Y, поэтому

Процесс распространения звуковых волн в газе можно считать адиабатическим, поэтому формула для скорости звука в газе имеет вид: ,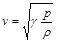

где р – давление в газе, g – показатель адиабаты.

Гидродинамическая теория волн на поверхности жидкости приводит к следующей формуле для фазовой скорости их распространения:

где g – ускорение свободного падения, l – длина волны.

Уравнение плоской бегущей волны имеет вид:

где x (x,t) – смещение частиц среды от положения равновесия;

А – амплитуда волны;

w – циклическая частота волны (w = 2 p f)

k – волновое число (k = 2p/l = v/w);

х – координата точки среды;

j₀ – начальная фаза волны.

Гармонические волны в однородных средах распространяются с некоторой постоянной скоростью v, равной

= ln = ,

которая называется фазовой скоростью волны. Если фазовая скорость волн в среде зависит от их длины, то это явление называют ДИСПЕРСИЕЙ ВОЛН.

Выражение, определяющее w = f (k) называется законом дисперсии или дисперсионным соотношением.

Уравнение сферической волны имеет вид:

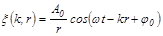где r – расстояние от центра волны до рассматриваемой точки среды.

ВОЛНОВОЕ УРАВНЕНИЕ – дифференциальное уравнение в частных производных, которое описывает процесс распространения волн в однородной изотропной среде:

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

ЭКСПЕРИМЕНТ 1. Исследование зависимости фазовой скорости распространения упругой волны от частоты

1. Откройте окно «Механические волны» и нажмите кнопку «Тип волн» – «Поперечные в верёвке».

2. Установите частоту колебаний 1,00 Гц и амплитуду колебания волны по таблице 1.

Таблица 1.

Бригада	1, 8	2, 7	3, 6	4, 5
Амплитуда, м	0,4	0,35	0,30	0,25

3. Определите фазовую скорость распространения поперечной волны на натянутой верёвке. Для этого:

Рис.1

а) с помощью секундомера определите время t прохождения цуга волны длиной 10l видимого на экране участка (рис.1) и запишите результат измерения в первую ячейку первой строки таблицы 2. Полезный совет: включите секундомер при пересечении любого (нулевого) гребня волны правой стороны рамки окна опыта «Гармоническая волна» и выключите при его при пересечении этой стороны десятого по счёту гребня волны.

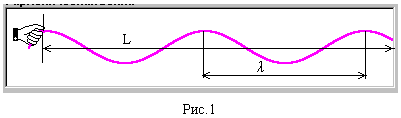
б) повторите это измерение ещё 4 раза и заполните первую строку табл. 2.

Таблица 2. Измерение времени распространения цуга волны

Частота волны, f Гц	Время распространения цуга волны t, с

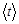
1,00
1,10
1.20
…
2,00

в) нажатием кнопки на экране монитора остановите волновой процесс и с помощью миллиметровой линейки измерьте длину волны l.

г) по формуле 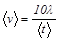определите среднюю фазовую скорость волны при частоты 1,00 Гц и запишите это значение в табл. 2 и 3 в столбец v_э.

1. Нажмите кнопку и, последовательно увеличивая частоту волны на 0,1 Гц, проделайте эти измерения для всего диапазона частот (1,00 – 2,00 Гц) и заполните таблицы 2 и 3.

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

1. По формуле v = ln вычислите для каждой частоты расчётную фазовую скорость волны v_т и запишите это значение в табл. 3 в строку v_т.

2. Постройте на одном графике зависимости экспериментальной v_э и расчетной v_т фазовой скоростей распространения волн от частоты колебаний f.

3. Из полученного графика определите зависимости 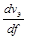и от частоты волны (дисперсию волн).

4. Сделайте выводы по результатам работы.

Таблица 3. Результаты измерений и расчётов

f, Гц	1,00	1,10	1,20	…	2,00
l, см
v_э,см/с
v_m см/с

ЭКСПЕРИМЕНТ 2. Экспериментальная проверка формулы фазовой скорости распространения гидродинамических поверхностных волн

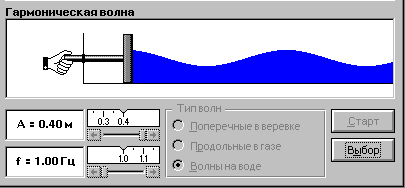
1. Откройте окно «Механические волны» и нажмите кнопку «Тип волн» – «Волны на воде».

2. Выполните измерения аналогичные измерениям п.п. 2-4 эксперимента 1 и запишите результаты измерений и расчётов в табл.4 и 5, аналогичные табл. 2 и 3 эксперимента 1.

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:

1. По формуле рассчитайте теоретическую фазовую скорость распространения волны для каждой измеренной длины волны и запишите эти значения в табл. 5 в строку v_m.

3. Из полученного графика определите зависимости 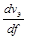и от частоты волны (дисперсию волн).

4. Сделайте выводы по результатам работы.

Вопросы и задания для самоконтроля

1. Определите, какую волну – продольную или поперечную – описывает уравнение ?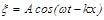

2. Что такое фазовая скорость волны? Напишите выражения для фазовой скорости волны.

3. Упругая волна переходит из среды, в которой фазовая скорость равна v в среду, в которой фазовая скорость в два раза больше. Определите, что при этом происходит с длиной волны и частотой?

4. Вдоль оси х распространяется плоская волна с длиной l. Определите наименьшее расстояние между точками среды, в которых колебания совершаются в противофазе.

5. На рис.4 показана «моментальная фотография» смещений частиц среды, в которой распространяется вдоль оси х упругая волна. Укажите направления скоростей частиц в точках А, В и С в случае: а) продольной волны; б) поперечной волны.

6. На рис.4 показана «моментальная фотография» смещений частиц среды, в которой распространяется вдоль оси х упругая волна. Укажите точки, в которых деформация среды: а) равна нулю; б) принимает максимальное значение. Укажите точки, в которых скорость смещения частиц среды: а) максимальна; б) минимальна.