Главная | Обратная связь | Поможем написать вашу работу!

Тема: геометрические характеристики плоских сечений

Нижнекамский химико-технологический институт (филиал)

Федерального государственного бюджетного образовательного учреждения

Высшего профессионального образования

«Казанский национальный исследовательский технологический университет»

Кафедра машин и аппаратов химических производств

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

Техническая механика

Выполнил

Студент группы № 2524

Столяров В.В.

_________________________

(подпись)

Принял

Алмакаева Ф.М.

_________________________

(преподаватель, Ф.И.О.)

(подпись)

Нижнекамск 2017

№ схемы	а,м	q,кН/м	α	β	γ	F, мм²	c = d/D
	1,4			1,2	1,8		0,87

Р=Р₁	М=М₁	М₂	М₃	М₄
22,4	31,36	31,36	28,224	18,816

ЗАДАНИЕ №1

ТЕМА: РАСТЯЖЕНИЕ-СЖАТИЕ

Проверить стержень на прочность (рис.1) и определить его полное перемещение.

Дано:

Материал стержня: СЧ 24-44

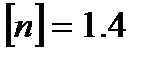допускаемый коэффициент запаса прочности

Расстояния между точками приложения сил: 0,5м

Полная длина стержня: 1,4 м

Решение

1. Определим величину нагрузок исходя их исходных данных:

Р = Р ₁ = ;

Р ₂ = ;

Р ₃ =

2. В данном случае стержень разбивается на 3 участка, площади поперечных сечений которых равны: F_I = 70 мм ² F_II=84 мм²F_III=126 мм ²

3. Применяя метод сечений, определяем значения продольных сил на каждом участке бруса:

N _zI =-P ₁ =-22,4 кН;

N _zII =-P ₁+ P ₂ =-22,4 + 44,8 =22,4 кН;

N _zIII =-P ₁+ P ₂+ P ₃ =-22,4 +44,8 +17,92=40,32 кН;

Строим эпюру продольных сил N _z(см. рис.1.б) по масштабу.

3. Определим нормальные напряжения на каждом участке ступенчатого стержня по формуле:

где - нормальное напряжение соответствующего участка стержня, МПа;

N _z - продольная сила соответствующего участка стержня, Н;

F - площадь поперечного сечения участка стержня, мм ²;

4. Проверяем условие прочности стержня, учитывая, что I участок работает на сжатие, II, III участки работают на растяжение.

где [s] - допускаемое нормальное напряжение растяжения (сжатия), МПа;

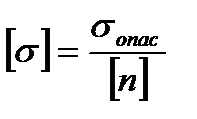где s _опас- опасное напряжение, МПа

Для хрупких материалов за опасное напряжение принимаем предел прочности. По ГОСТ 1412 - 85 выписываем механические характеристики серого чугуна марки СЧ 24 - 44:

= 250 МПа - предел прочности при растяжении;

= 950 МПа - предел прочности при сжатии;

[n] - предельный коэффициент запаса прочности;

> условие прочности не выполняется

, > - условие прочности не выполняется

Определяем необходимое сечение стержня на этих участках:

Принимаем F_I=71мм²

Принимаем F_II=270мм²

Принимаем F_Ш=486мм²

5. Определение перемещений начинаем с заделки, где оно равно 0. Перемещение произвольного сечения на расстоянии z равно абсолютному удлинению части стержня, которая заключена между этим сечением и заделкой.

Перемещение произвольного сечения вычисляется по формуле:

Где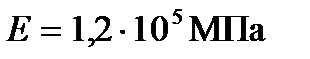

Перемещение Ш участка относительно заделки равно:

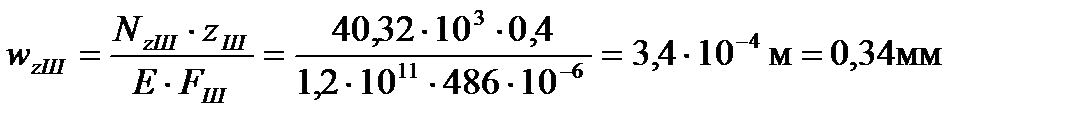
Перемещение II участка равно:

Перемещение I участка равно:

Определяем полное перемещение как сумму удлинений (укорочений) отдельных участков:

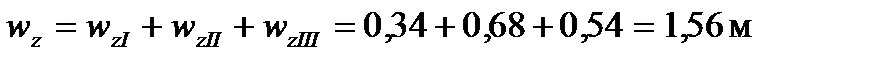
Положительное значение w_z показывает, что стержень удлинился.

ЗАДАНИЕ №2

ТЕМА: КРУЧЕНИЕ

Рис.2. Расчетная схема вала

Для заданной схемы вала требуется:

· Построить эпюры внутренних силовых факторов

· Подобрать диаметр вала из условия прочности

· Определить углы закручивания и построить эпюры

· Определить относительные углы закручивания и проверить на жесткость при циклическом нагружении

Дано: схема балки №4, материал вала Ст20

Решение

1. Определение расчетных параметров:

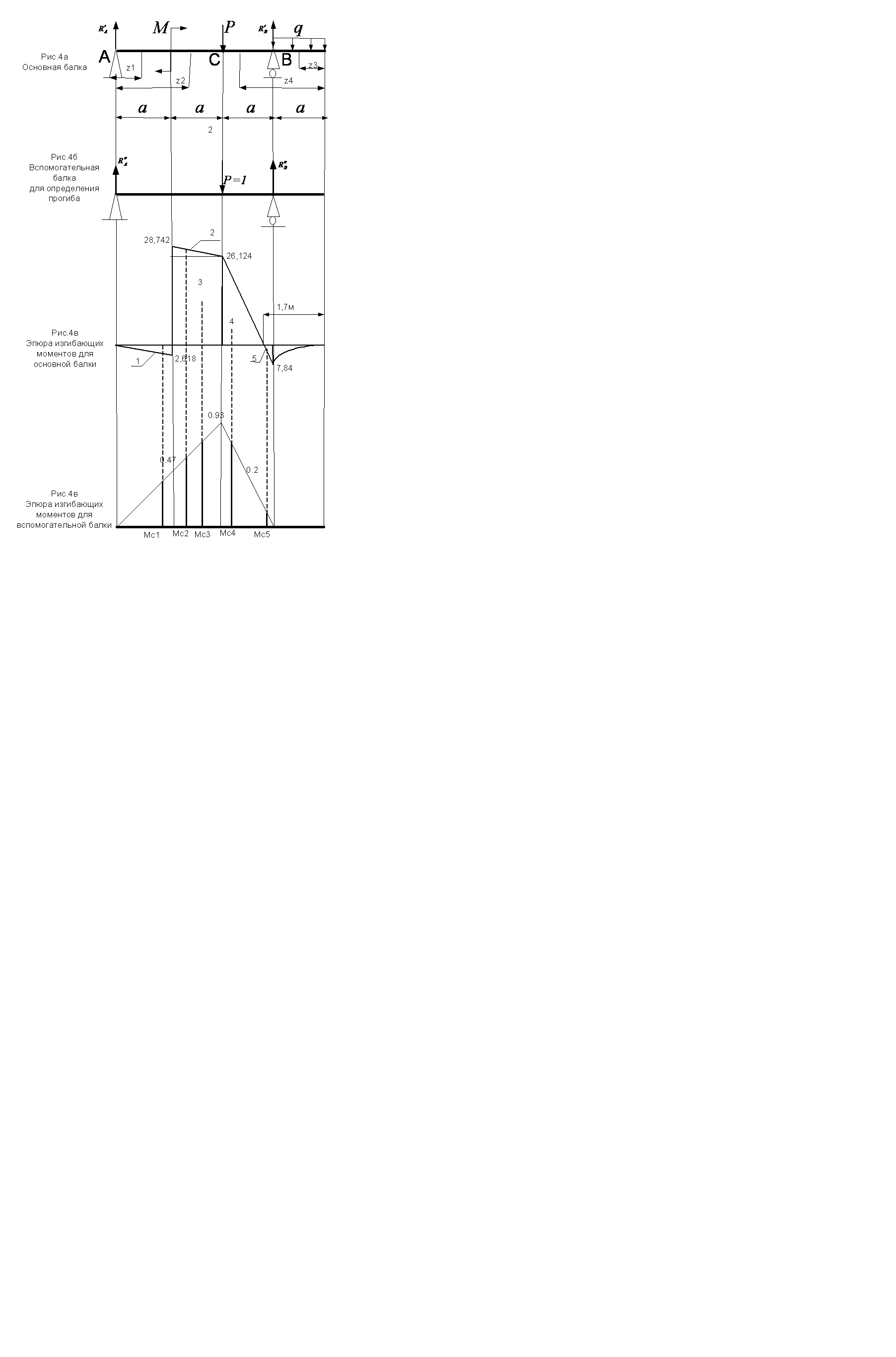
М=М₁= кНм.

М₂=М₁=31,36 кНм

М₃=0,9М₁=28,224 кНм

М₄=0,6М₁=18,816 кНм

2. Разбиваем вал на участки 1, 2, 3, 4.

3. Применяя метод сечений, определяем значения крутящих моментов на участках вала:

1 участок: (0 £ z ₁ £ а)

S М =- Т₁ + М₁= 0

Т₁= М₁= 31,36 кН× м

2 участок: (а £ z ₂ £ 2а)

S М = - Т₂ + М₂ +М₁= 0

Т₂=М₂ + М₁=31,36+31,36 =62,72 кН× м

3 участок: (2а £ z₃ £ 3а)

S М = - Т₃ +М₂+ М₁ + М₃= 0

Т ₃ = М₂ +М₁ + М₃=31,36 +31,36 +28,224 =90,944 кН× м

4 участок: (3а £ z ₄£ 4а)

S М = - Т ₄ -М ₄+М ₃+М ₂+М ₁= 0

Т₄ =-М ₄ +М ₃+М ₂+М ₁=-18,816 +28,224+31,36 +31,36 =72,128 кН× м

Эпюру крутящих моментов Т по длине вала строим в масштабе (смотри рис.2, б)

4. Определим диаметр вала из условия прочности при кручении:

где _max- максимальное расчетное напряжение, МПа;

- абсолютная величина максимального крутящего момента, Н × м;

- полярный момент сопротивления сечения вала, мм ³;

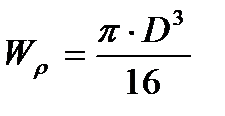
- допускаемое касательное напряжение, МПа;

= (0,7…….0,8) × [s],

где [s] - допускаемое нормальное напряжение, МПа;

где s _тек- предел текучести материала вала, МПа;

s _тек= 250 МПа, для стали марки Ст 20;

[n] - предельный коэффициент запаса прочности,

принимаем [n] = 3;

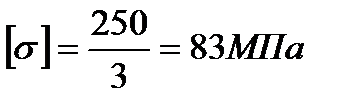
= (0,7…….0,8) × 83 = (58.....66) МПа, принимаем = 62 МПа.

;

= 0,195 м = 19,5 см.

Принимаем диаметр вала =20см =200 мм,

5. Жесткость вала:

G=8·10¹⁰H/м²– модуль сдвига для стали

I_p=πD⁴/32 -полярный момент инерции

Определим углы закручивания, начиная с заделки:

Определим относительный угол закручивания на каждом участке.

При циклическом нагружении

условие жесткости не выполняется, для того, чтобы вал деформировался в заданных пределах, необходимо увеличить его диаметр

Ответ: = 227мм

6. Строим эпюру углов закручивания. Рис.2в

ЗАДАНИЕ №3

ТЕМА: ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

Дано:

1) составное поперечное сечение рис.3

2) Размеры сечения (№ профиля) – таблица 2.

№ схемы по рис.3	Лист bxh, мм	№ швеллера	№ уголка
	16х330

Требуется:

1) Определить положение центра тяжести составного сечения;

2) Вычислить моменты инерции всего сечения относительно центральных осей;

3) Определить положение главных центральных осей

4) вычислить главные моменты инерции;

1. Составное поперечное сечение можно разбить на три простых фигуры:

1 – прямоугольник 16 х 330;

2 – швеллер № 18;

3 – уголок № 16.

2. Определение площади листа: F ₁ = b x h = 16 × 330 = 5280 мм ²= 52,8 cм ²

3. По ГОСТ 8239 - 89 и ГОСТ 8509 - 93 выписываем технические

характеристики швеллера № 18 и равнополочного уголка № 16.

Швеллер № 18

h₂ = 180 мм, b₂ = 70 мм, d = 5,1 мм, t = 8,7 мм, F ₂= 20,7 cм ², J _X2= 86 cм ⁴,

J _У2= 1090 cм ⁴, z ₀₂ = 1,94 см.

Уголок № 16

b =160 мм, d = 10 мм, F ₃= 31,43 cм ², J _X3= 774,24 cм ⁴, J _{X0 max} = 1229,1 cм ⁴,

J _{У0 min}= 319,38 cм ⁴, z ₀₃ = 4,3 см,

4. Исходя из размеров выполняем сечение в масштабе 1: 2 (смотри рисунок)

5. Проводя систему координат хОу, для каждой фигуры находим положения центров тяжести С ₁, С ₂, С ₃ и определим координаты центров тяжести:

х_с1= b₁/2 = 16/2 = 8 мм;

У _С1= h ₁/2 = 330/2 = 165 мм;

х_{с 2} = b ₁+ h ₂/2 = 16 + 90 = 106 мм;

У _С2= b ₃+ z ₀₂=160+19,4= 179,4 мм;

х_{с 3}= b ₁+z ₀₃= 16 + 43 = 59 мм;

У _С3= b ₃–z ₀₃= 160- 43 = 117 мм.

6. Вычислим координаты центра тяжести составного поперечного сечения по формулам:

;

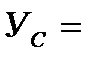
где F - площадь фигуры, cм ²;

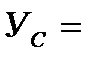
7. Вычислим моменты инерции сечения относительно центральных осей:

+ + ;

+ + ,

где 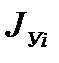- моменты инерции i - ого элемента сечения относительно его осей, параллельных осям и ;

а _i,d_i - координаты (расстояния от центральных осей до своих осей);

а ₁= У_с1- У_с = 165 – 153,46 =11,54 мм

d ₁= X_с1- X_с= 8 - 42,6 = - 34,6 мм

а ₂= У_с2- У_с= 179,4 - 153,46 = 25,94 мм

d ₂= X_с2- X_с = 106 - 42,6 = 63,4 мм

а ₃= У_с3- У_с = 117 – 153,46 = -36,46 мм

d ₃= X_с3- X_с = 59 - 42,6 = 16,4 мм

Определим моменты инерции листа, имеющего прямоугольное сечение:

= + + +

+ + +

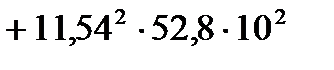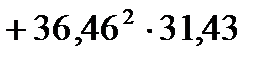
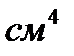
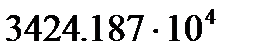
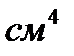
8. Определим величину центробежного момента инерции уголка, так как оси Х и У не являются главными:

= =

9. Определим величину центробежного момента инерции относительно центральных осей: и :

= + + + + +

Учитывая, что = 0 и = 0, перепишем формулу в следующем виде:

= + + +

= + + -

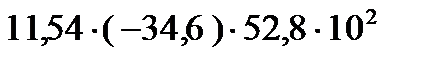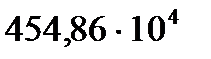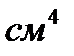
10. Определим направление главных центральных осей и .

Главные оси и проходят через центр тяжести С и повернуты относительно центральных осей на угол a ₀, величина которой определяется по формуле:

= -15,5⁰ Þ 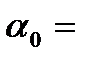-7,7 ⁰

11.Показываем на рисунке направление главных центральных осей и .

Так как угол , то главные центральные оси и получаем поворотом осей и по ходу часовой стрелки.

12. Определяем главные моменты инерции сечения:

+ - ;

+ + ;

+ +

= + -

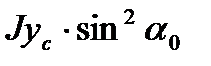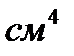
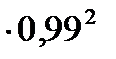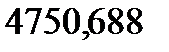
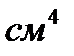
При правильном вычислении выполняется равенство:

+ = +

+ = +

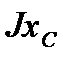Условие выполняется, значит, задача решена правильно.

Рис3. Эскиз составного сечения

ЗАДАНИЕ №4

ТЕМА: ИЗГИБ

Для балки построить эпюры внутренних силовых факторов используя метод сечений

Определить прогиб посередине балки используя правило Верещагина (энергетические способы определения перемещений). Жесткость балки определить исходя из размеров сечения и материала. Сечение двутавр №10

Дано:

а=1,4м q= 8кН/м Р=22,4 кН М= 31,36 кНм

Материал балки - Ст 10

Рис.4 Схема балки

Решение:

1. Определяем опорные реакции, применяя уравнения равновесия статики:

Основная балка: (рис.4а)

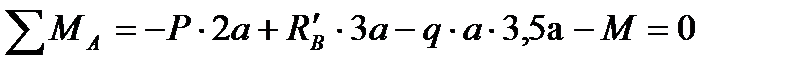
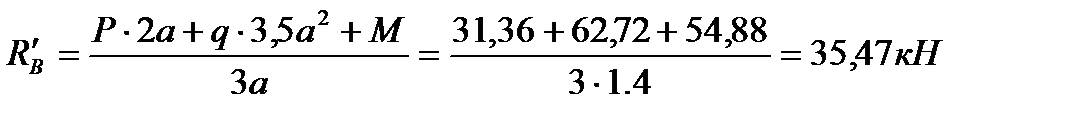
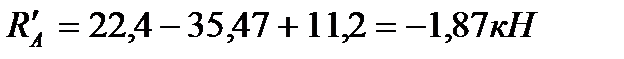
Вспомогательная балка для определения прогиба: (рис.4б)

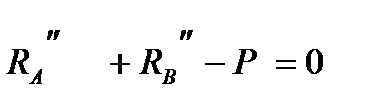
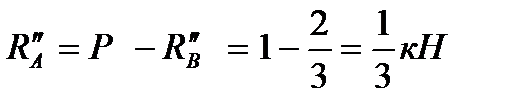
2. Разбиваем балку на 4 участка.

Применяя метод сечений, определяем значения поперечных сил Q_уи изгибающих моментов М_Х на участках балки

I участок: (0 £ z ₁ £ 1, 4)

Основная балка:

Вспомогательная балка для определения прогиба:

II участок: (1,4 £ z₂ £ 2,8)

Основная балка:

Вспомогательная балка для определения прогиба:

III участок: (0 £ z ₃ £ 1,4)

Основная балка:

Вспомогательная балка для определения прогиба:

IV участок: (1,4 £ z ₃ £ 2,8)

Основная балка:

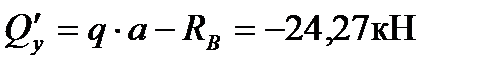
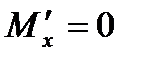
Вспомогательная балка для определения прогиба:

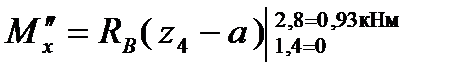
Эпюру поперечных сил и изгибающих моментов строим в масштабе:

Эпюру изгибающих моментов М _х для основной и вспомогательной балки для определений прогиба строим в масштабе смотри рисунок 4в, 4г.

3. Для Ст 20 -модуль упругости

По ГОСТ 8239 - 95 выписываем характеристики двутавра № 10:

, А = 12 , , , , , ,

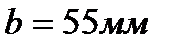Тогда жесткость балки равна:

Метод Верещагина

Перемещения по методу Верещагина определяются по формуле:

где ω- площадь эпюры изгибающих моментов для основной балки

Мс-высота (ордината) внутреннего момента под центром тяжести основной балки на единичной эпюре, которую строим для вспомогательной балки.

Определяем площади грузовых эпюр и единичные моменты под центрами тяжести грузовой эпюры (для прогиба в точке С):

1 треугольник: ω=0,5·1,4·2,618=1,8326 = 2/3·0,47=0,31 ω = 0,568

2 треугольник: ω=0,5·1,4(28,742-26,124)=1,8326 =1/3·(,93-0,47)+0,47=0,62 ω =1,142

3 прямоугольник: ω=1,4·26,124=36,573 =0,47+1/2(0,93-0,47)=0,7 ω =25,6

4 треугольник: ω=0,5(2,8-1,7)·26,124=14,368 =0,2+(0,93-0,2) ·2/3 =0,68 ω =9,866

5 треугольник: ω=0,5(1,7-1,4)·7,84=1,176 =2/3·0,2=0,13 ω =0,156

Чтобы определить прогиб в точке С нужно сложить все произведения, рассчитанные по формуле Верещагина и разделить на жесткость балки, в соответствии с правилом знаков треугольник 1и 5 берем со знаком «-», остальные - со знаком «+»

ЗАДАНИЕ № 5

Воспользуйтесь поиском по сайту: