|
Результаты выполнения программы
|
|
|
|
ОТЧЁТ
по лабораторной работе №1
«Программная реализация рекурсивных функций»
по дисциплине
«Информационные технологии и программирование»
Выполнил: студент гр. Р/б-11-о
Ивашкив Анна Владимировна
Вариант №9
Защитил с оценкой: ______
Принял: ст. преподаватель Тыщук Ю.Н.
Севастополь
2016
СОДЕРЖАНИЕ
1. Описание лабораторной работы 3
1.1. Цель работы 3
1.2. Индивидуальное задание 3
1.3. Теоретические сведения 3
2. Выполнение лабораторной работы 4
2.1. Структурная схема алгоритма работы программы 4
2.2. Текст программы 7
2.3. Таблица переменных 9
2.4. Результаты выполнения программы 9
Выводы 10
|
|
|
Приложение А. Проверка результатов выполнения программы
в приложении MathCAD 11
Описание лабораторной работы
Цель работы
Цель работы — изучение особенностей составления и использования рекурсивных функций в языках программирования С / С ++. Получение практических навыков реализации алгоритмов, использующих рекурсивные функции, средствами языков программирования С / С ++.
Индивидуальное задание
Вариант №9. Составить схему алгоритма и написать на языке С / С ++ программу вычисления суммы n элементов ряда, полученного при разложении функции f (x), используя рекурсивные функции:
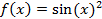 ;
;
 ;
;
 .
.
Теоретические сведения
Рекурсивной называют функцию, которая вызывает саму себя. Такая рекурсия называется прямой. Существует косвенная рекурсия, когда две или более функций вызывают друг друга. Когда функция вызывает себя, в аппаратном или программном стеке создаётся копия значений её параметров, как и при вызове обычной функции, после чего управление передаётся первому исполняемому оператору функций. При повторном вызове этот процесс повторяется. Для завершения вычислений каждая рекурсивная функция должна содержать хотя бы одну нерекурсивную ветвь алгоритма, заканчивающуюся оператором возврата. При завершении функции соответствующая часть стека освобождается, и управление передаётся вызывающей функции, выполнение которой продолжение с оператора, следующего за рекурсивным вызовом. Объявление, описание и вызов рекурсивных функций выполняется по тем же правилам, что обычных функций.
Выполнение лабораторной работы
Структурная схема алгоритма работы программы
Структурная схема алгоритма решения задачи представлена на рис. 2.1, рис. 2.2 и рис. 2.3.
|
|
|

Рис. 2.1 — Структурная схема алгоритма программы (функция main)

Рис. 2.2 — Структурная схема алгоритма программы
(функции sum _ of _ series)

Рис. 2.3 — Структурная схема алгоритма программы
(функции term _ of _ series)

Рис. 2.4 — Структурная схема алгоритма программы (функция factorial)
Текст программы
#include <conio.h>
#include <iostream.h>
#include <math.h>
double sum_of_series(double x, int k, int n);
double term_of_series(double x, int k);
long int factorial (long int k);
void main()
{
int n;
double x,sum;
clrscr();
cout<<"Vvedite znachenie argumenta 'x':";cin>>x;
cout<<"Vvedite kolichestvo chlenov ryada 'n': ";cin>>n;
sum=sum_of_series(x,1,n);
cout<<"Summa chlenov ryada: "<<sum<<endl;
cout<<"funkcia: "<<pow(sin(x),2)<<endl;
getch();
return;
}
double sum_of_series(double x, int k, int n)
{
if(k<=n)
{
return (term_of_series(x,k)
+sum_of_series(x,k+1,n));
}
else
{
return 0;
}
}
double term_of_series(double x, int k)
{
double result = 0;
result=pow(-1,k+1)*pow(2,2*k-1)*pow(x,2*k)
/factorial(2*k);
cout<<"Chlen ryada:"<<k
<<"Znachenie:"<<result<<endl;
return result;
}
long int factorial (long int k)
{
return ((k==0 || k==1)?1:k*factorial(k-1));
}
Таблица переменных
В программе использованы переменные, представленные в таблице 2.1.
Таблица 2.1 — Используемые переменные
| Переменная | Тип | Значение |
| x | d ouble | Значение аргумента |
| k | int | Порядковый номер |
| n | int | Количество суммируемых членов ряда |
| sum | double | Сумма членов ряда |
Результаты выполнения программы
Результат выполнения программы изображен на рис. 2.5.

Рис. 2.5 — Изображения окна UserScreen при выполнении программы
Выводы
Для вычисления суммы ряда, согласно заданию, была использована рекурсивная функция sum _ of _ series, которая в своем теле содержала вызов самой себя. При разработке этой функции были изучены основные принципы использования рекурсивных функций и их основные особенности:
— все функции языка С ++ (кроме функции main) могут быть использованы для построения рекурсии;
— в тексте рекурсивной функции обязательно должен быть выполнен условный оператор, который при определенных условиях вызовет завершение функции;
— обработка вызова рекурсивной функции не отличается от вызова функции обычной: перед вызовом функции в стек помещаются её аргументы, затем адрес точки возврата, затем, уже при выполнении функции — автоматические переменные, локальные относительно этой функции.
|
|
|
Полученные результаты расчета суммы ряда сравнены со значением исходной функции, а также с данными, полученными при расчете в программе MathCAD. Полученные значения близки. Заданное количество точек аппроксимирующего ряда позволяет получить значение близкое к аппроксимируемой функции (см. Приложение А, рис. А.1).
Таким образом, цель лабораторной работы достигнута, задание выполнено полностью.
ПРИЛОЖЕНИЕ А
Проверка результатов выполнения программы в приложении MathCAD
|
|
|
|
|
|
|
|
|
|
| Рис. А.1. — График пересечений заданных функций |
|
|
|
|
|
|
|
|
|