Изучение поведения функций.

Дифференциальное исчисление

Дифференциальное исчисление совместно с интегральным исчислением составляет важнейшую часть математического анализа. Центральным понятием дифференциального исчисления является понятие производной. К нему приводят соображения механического и геометрического характера.

Пусть путь точки выражается как функция от времени . Возникает вопрос, чему равна скорость точки в момент времени t₀. Для равномерного движения скорость равна пути, деленному на время. Взяв промежуток времени , можно вычислить на нем среднюю скорость . Чем короче отрезок времени , тем точнее средняя скорость соответствует мгновенной скорости при . По этой причине можно определить мгновенную скорость как

Геометрическая задача, приводящая к понятию производной, связана с проведением касательных к произвольной кривой. Пусть нужно провести касательную к графику кривой в точке , где . Задача решается так: выберем на графике точку M и проведем секущую MM₀. Ее тангенс угла наклона . При движении точки M к точке M₀ секущая переходит в касательную, следовательно, тангенс ее угла наклона равен .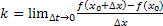

Математическое определение производной

Производной функции в точке называется предел

Механический смысл производной – скорость изменения функции. Геометрический смысл производной – тангенс угла наклона касательной.

Итак, если функция имеет производную, то к ней можно провести касательную. Интуитивно ясно, что в этой точке график не может иметь излома. По этой причине дифференцируемые во всех точках функции называются гладкими.

Если функция имеет производную в каждой точке, где она определена, то множество значений производной образует новую функцию, которая называется производной и обозначается через . Часто под производной понимают именно функцию.

Значение производной связано со следующим обстоятельством: если уравнение прямой y = kx + b, то при k > 0 прямая указывает своим направлением, что функция, касательной к которой является y = kx + b, возрастает, а при k < 0 убывает. При k = 0 можно ожидать, что функция меняет фазу возрастания на фазу убывания или наоборот, т. е. имеет экстремум. Итак, производная – важнейший инструмент изучения поведения функций.

Первой задачей, связанной с использованием производной, является вычисление производных от элементарных функций, и также установление общих свойств производных.

Производные элементарных функций

1.

2.

3.

4.

5.

6.

7.

8.

Свойства производных

1. Производная суммы функций равна сумме их производных

2. Производная функции, умноженной на число, равна производной этой функции, умноженной на число

3. Производная произведения функций u(x) и v(x)

4. Производная частного

Следствие:

5. Производная сложной функции

6. Для обратной функции имеем

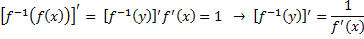
Следствие:

С понятием производной связано еще одно понятие – дифференциал. Это понятие выражает наличие линейной составляющей у приращения функции. Если Δy=A Δx+o(Δx), где o(Δx) – бесконечно малый член такой, что o(Δx)/ Δx →0, при Δx→0, говорят, что функция дифференцируема, а выражение A Δx называется дифференциалом. Обозначается символом dy.

Теорема. Для того, что бы функция была дифференцируемой, необходимо и достаточно, что бы существовала конечная производная y′(x₀). При этом коэффициент A= y′(x₀).

Дифференциал независимой переменной x – это приращение Δx. Его обозначают через dx. Из этого следует dy= y′(x₀)dx. Отсюда запись для производной y′ = dy/dx.

Геометрически Δy – приращение кривой, а dy – приращение касательной. При приближенных вычислениях можно использовать дифференциал следующим образом

Δy= f(x₀+ Δx) – f(x₀) ≈ f’(x₀) Δx => f(x₀+ Δx) ≈ f(x₀)+f′(x₀) Δx

Пример.

Вычислить . Рассмотрим функцию , . Пусть x₀ = 9, Δx = 1, тогда .

Второе приближение: , , тогда

.

Основные теоремы:

Говорят, что функция y = f(x) возрастает (аналогично определение убывания) в точке x₀, если f(x) < f(x₀) при x < x₀ и f(x) > f(x₀) при x > x₀ в некоторой окрестности x₀.

Лемма. Если функция имеет производную f'(x) > 0, то она возрастает в точке x₀.

Действительно в некоторой окрестности точки x₀ верно неравенство (f(x) – f(x₀))/(x – x₀) > 0, т.е. знаки разностей, стоящих в числителе и знаменателе, соответствуют.

Теорема Ферма. Пусть функция f(x) определена на отрезке и в его внутренней точке с принимает наибольшее (наименьшее) значение. Если функция дифференцируема, то f(c)=0.

Допустив, что f′(c) ≠ 0, получим, что f(c) или >0 и функция возрастает в точке x₀, или <0 и функция убывает, чего не может быть.

Теорема Ролля.

Пусть функция определена на отрезке [a; b] вместе со своей производной и f(a) = f(b). Тогда между a и b существует точка с такая, что f'(c)=0.

Если f(x)=const, то f′=0 в любой точке отрезка. В противном случае по 2-й теореме Вейерштрасса достигается наибольшее и наименьшее значения. Одно из них не равно f(a), следовательно, наибольшее и наименьшее значения f(x) принимает в некоторой внутренней точке с отрезка [a; b]. По теореме Ферма f′(c)=0.

Теорема Лагранжа.

Пусть функция f(x) со своей производной определена на отрезке [a; b] тогда внутри отрезка найдется точка с, такая, что f′(с)= (f(b) – f(a))/(b – a).

Следует рассмотреть функцию F(x)=f(x) – f(a) – ((f(b) – f(a))/(b – a))(x – a). Она удовлетворяет теореме Роля, а, следовательно, F′(x)=f′(x) – (f(b) – f(a))/(b –a) обращается в некоторой точке с в ноль. Формула Лагранжа называется формулой конечных приращений. Для отрезка [x₀, x₀+ Δx] она имеет вид (f(x₀, x₀+ Δx)-f(x₀))/ Δx = f′(x₀+θ Δx), где θ заключено между 0 и 1.

Теорема Коши.

Пусть функции f(x) и g(x) дифференцируемы на отрезке [a; b] и g(x) ≠ 0 на том отрезке. Тогда .

Рассмотрим функцию F(x) = f(x) – f(a) – . F(a) = F(b) и . По теореме Роля существует точка такая, что =0. Это и есть искомая точка.

Производные высших порядков. Если взять производную от функции y = f(x), то получится новая функция От нее тоже можно попытаться взять производную – вторую: Продолжая этот процесс, можно получить производные высших порядков y⁽ⁿ⁾ =f⁽ⁿ⁾ (x). Иногда этот процесс обрывается. По этой причине в теоремах заранее оговаривают, что имеют ввиду функцию, дифференцируемую нужное число раз.

Правило Лопиталя. Пусть при и при . Тогда в случае существования производных и ( имеем: . Действительно, . Остается перейти к пределу при .

Ряд Тейлора. Для удобства вычислений было бы желательно любую функцию представить как сумму бесконечного степенного ряда по аналогии с многочленами.

f(x)=a₀+a₁(x-x₀)+a₂(x-x₀)²+…

Допустим, что функция дифференцируема бесконечное количество раз. Тогда

……………………………………..

…………………………………….

Таким образом, коэффициенты разложения должны выражаться через значения производных функции в точке, в окрестности которой функция разлагается в ряд. Можно формально записать связь функции и ряда:

+…

Однако, для настоящего разложения нужно установить, что сумма ряда действительно сходится к значению функции. Для этого следует изучить разность – это так называемый остаточный член.

Заменим x₀ на переменную z и получим функцию .

Далее φ(x₀) = r_n(x) и φ(x) = 0. Вычислением легко показать, что . Если взять произвольную дифференцируемую функцию ψ^-1(z) ≠ 0 в промежутке (x₀, x), по теореме Коши , откуда r_n(x)= , где . При получаем – остаточный член в форме Лагранжа.

Простые разложения получаются для ряда элементарных функций.

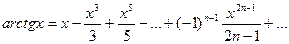
Изучение поведения функций.

Поделиться:

Воспользуйтесь поиском по сайту: