Описание лабораторного макета

Лабораторная работа 2.3

ИССЛЕДОВАНИЕ АЛГОРИТМОВ ЭФФЕКТИВНОГО КОДИРОВАНИЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ СООБЩЕНИЙ

Цель работы

1.1 Изучение информационных характеристик источника дискретных сообщений и принципов эффективного кодирования сообщений.

1.2 Изучение алгоритмов и исследование особенностей эффективного кодирования Хаффмана и Шеннона-Фано.

Ключевые положения

2.1 Информационные характеристики источника дискретных сообщений.

Под информацией понимают совокупность неизвестных для получателя сведений. Для определения количественной меры информации в теории и технике связи в основу положены вероятностные характеристики передаваемых сообщений, которые показывают их степень неопределенности.

Таким образом, количество информации I (a) в сообщении a с вероятностью его появления P (a) определяется как

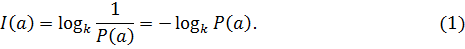
Логарифмическая мера обладает свойством аддитивности (количество информации, которое содержится в нескольких независимых сообщениях равно сумме количества информации каждого сообщения). Т.к. 0 < P (a) 1, то величина I (a) является неотрицательной и конечной. Если P (a) = 1, то количество информации равно нулю (сообщение об известном событии никакой информации не несет).

Единицы измерения количества информации зависят от выбора основания логарифма. Обычно используют основание логарифма k = 2. В этом случае информация измеряется в двоичных единицах (дв. ед.), или битах (1 бит определяется как количество информации в сообщении, вероятность которого P (a) = 0,5).

Знание количества информации в отдельных сообщениях недостаточны для оценки информационных процессов, требуется оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик источника является энтропия.

Энтропия источника H (A) – это среднее количество информации в одном знаке (измеряется в бит/знак). Таким образом, среднее количество информации определяется как математическое ожидание для M_A независимых знаков

Физически энтропия выражает меру неопределенности состояния источника сообщений, она является объективной информационной характеристикой источника.

Из выражения (2) следует, что энтропия неотрицательна. При этом энтропия равна нулю только тогда, когда вероятность одного из сообщений равно 1, а остальные имеют нулевую вероятность.

Энтропия достигает максимального значения в случае, когда все передаваемые M_A сообщений равновероятны и независимы:

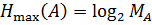. (3)

В общем случае для энтропии справедливо выражение .

Очень часто . Тогда дв. ед. /знак. Следовательно, при передаче информации двоичными символами, каждый символ не может переносить более чем 1 дв. ед.

Избыточность источника характеризует уменьшение энтропии источника по сравнению с максимальной энтропией. Основные причины избыточности:

- различные вероятности отдельных знаков;

- наличие статистических связей между знаками источника.

Количественно избыточность источника оценивается коэффициентом избыточности

Производительность источника R _и, бит/с – это среднее количество информации, которое выдает источник в единицу времени

где T _ср – средняя длительность одного знака и определяется как

где T_i – длительность i -го знака.

 

 

2.2 Алгоритмы эффективного кодирования сообщений.

Согласно с теоремой кодирования Шеннона для канала без помех дискретный источник сообщений с алфавитом A = { a ₁, a ₂,…, a_k,} и вероятностями сообщений P (a ₁), P (a ₂),…, P (a_k) может быть закодирован эффективным префиксным кодом таким образом, что

(7)

где – средняя длина кодовых комбинаций и определяется как

Теорема кодирования Шеннона для канала без помех указывает на возможность создания методов эффективного кодирования дискретных сообщений, в результате которых средняя длина кодовой комбинации не может быть меньше энтропии, но может приближаться к ней сколь угодно близко.

Т.к. в большинстве случаев знаки имеют разные вероятности, то кодовые комбинации должны иметь различные длины с целью уменьшения избыточности передаваемых сообщений. Такое кодирование называется эффективным, или сжатием информации.

Для оценки эффективности выбранного метода кодирования вводится понятие эффективность кодирования

Также можно рассчитать коэффициент сжатия по сравнению с равномерным кодом

где – минимальное целое число, при котором выполняется равенство-неравенство.

Основной принцип эффективного кодирования состоит в том, что более вероятным знакам должны соответствовать более короткие кодовые комбинации, а знакам с малой вероятностью – более длинные.

Префиксным называется кодирование, в результате которого ни одна из коротких кодовых комбинаций не является началом более длинных комбинаций. Тем самым префиксное кодирование обеспечивает однозначную разделимость кодовых комбинаций при декодировании.

 

Алгоритм Хаффмана. Используется для кодирования независимых знаков. В начале алгоритма Хаффмана должна быть таблица частот (вероятностей) знаков в сообщении. На основании этой таблицы строится дерево кодирования Хаффмана по следующему алгоритму:

1. Все знаки располагаются в порядке убывания их вероятностей сверху-вниз (каждому соответствует свой узел дерева).

2. Два знака с наименьшими вероятностями ветками объединяются в составной знак с суммарной вероятностью объединяемых знаков (далее два участвовавших в объединении знака не рассматриваются, а составной знак рассматривается наравне с остальными).

3. Одной ветке, например верхней, присваивается символ “1”, другой ветке – “0” (или наоборот).

4. Шаги, начиная со второго, повторяются до тех пор, пока в списке знаков не останется только один. Он и будет считаться корнем дерева.

Для определения кодовой комбинации каждого из знаков, входящего в сообщение, необходимо пройти путь от корня дерева к первоначальным узлам (знакам), накапливая биты (0 или 1) при перемещении по ветвям дерева.

Пример 1. Задан источник дискретных сообщений с объемом алфавита M_A = 6 с вероятностями знаков: P (А)=0,3; P (Е)=0,25; P (В)=0,22; P (Г)=0,1; P (Д)=0,08; P (Б)=0,05. Построить дерево кодирования Хаффмана и определить кодовые комбинации знаков сообщения.

Построим дерево кодирования Хаффмана

Рисунок 1 – Дерево кодирования Хаффмана

 

На основании кодового дерева запишем соотствующие знакам кодовые комбинации: А – 11; Е – 10; В – 00; Г – 010; Д – 0111; Б – 0110.

 

Алгоритм Шеннона-Фано. Также используется для кодирования независимых знаков. В начале алгоритма Шеннона-Фано должна быть таблица частот (вероятностей) знаков в сообщении.

1. Все знаки располагаются в порядке убывания их вероятностей сверху-вниз.

2. Вся группа знаков делится на две подгруппы, суммарные вероятности знаков которых приблизительно равны.

3. Всем знакам верхней подгруппы присваивается “0”, нижней – “1”.

4. Шаги, начиная со второго (применительно к образовавшимся подгруппам), повторяются до тех пор, пока в подгруппах останется по одному знаку.

Кодовая комбинация получается, как последовательность бит, соответствующих группам, в которых участвовал при разбиении данный символ и выписывается слева-направо.

Пример 2. Задан источник дискретных сообщений с объемом алфавита M_A = 6 с вероятностями знаков: P (А)=0,3; P (Е)=0,25; P (В)=0,22; P (Г)=0,1; P (Д)=0,08; P (Б)=0,05. Построить таблицу разбиений на подгруппы по алгоритму Шеннона-Фано и определить кодовые комбинации знаков сообщения.

В таблице 1 проиллюстрируем принцип алгоритма Шеннона-Фано.

Таблица 1 – алгоритм Шеннона-Фано

Знак ai	Вероятность P (ai)	Подгруппы	Кодовые комбинации
I	II	III	IV
А	0,3
Е	0,25
В	0,22
Г	0,1
Д	0,08
Б	0,05

 

Недостатки алгоритмов Хаффмана и Шеннона-Фано:

- если до начала кодирования сообщений не известны вероятности знаков, то требуется два прохождения по передаваемой последовательности: одно для составления таблицы вероятностей и кода, второе для кодирования;

- необходимость передачи таблицы кодовых комбинаций (кода) вместе со сжатым сообщением, что приводит к уменьшению суммарного эффекта сжатия;

- для двоичного источника сообщений с энтропией меньше 1 непосредственное применение кода Хаффмана/Шеннона-Фано не дает эффекта;

- избыточность закодированного сообщения равна нулю только в случае, когда вероятности кодируемых знаков являются целыми отрицательными степенями двойки (1/2; 1/4; 1/8 и т.д).

В большинстве случаев, средняя длина кодовой комбинации при сжатии методом Шеннона-Фано такая же, как и при сжатии методом Хаффмана. Но существуют случаи, когда в отличие от метода Хаффмана, кодирование методом Шеннона-Фано не будет оптимальным.

3 Ключевые вопросы

3.1 Что такое информация и как определяется ее количество?

3.2 Что такое энтропия источника? Когда она максимальна?

3.3 Что такое избыточность источника и каковы ее причины?

3.4 Сформулировать теорему кодирования Шеннона для канала без помех.

3.5 В чем заключается основной принцип эффективного кодирования?

3.6 Что такое префиксность?

3.7 Описать алгоритм кодирования методом Хаффмана.

3.8 Описать алгоритм кодирования методом Шеннона-Фано.

3.9 Перечислить недостатки методов эффективного кодирования Хаффмана и Шеннона-Фано.

Домашнее задание

4.1. Выучить раздел “Эффективное кодирование дискретных источников” по конспекту лекций и ключевым положениям. Также можно воспользоваться литературой [1, с. 295-298; 2, с. 307-310; 3, с. 876-885].

4.2. Задан источник дискретных сообщений с объемом алфавита M_A = 5. Количество появлений знаков задано в таблице 2. Построить дерево Хаффмана (таблицу разбиений на подгруппы методом Шеннона-Фано), записать кодовые комбинации, определить H (A), K _изб, , μ и η.

Таблица 2 – Количество появлений знаков алфавита дискретного источника

№ варианта	Количество появлений знаков алфавита дискретного источника
А	Б	В	Г	Д

4.3. Подготовиться к обсуждению по ключевым вопросам.

Лабораторное задание

5.1. Запустить программу “Кодирование Хаффмана”/“Кодирование Шеннона-Фано”, используя иконку “Лабораторные работы” на рабочем столе, а затем папку ОТПИ (ТИ). Изучить схему макета.

5.2. Исследовать источник дискретных равновероятных сообщений. Установить объем алфавита равным 5, затем создать поля, и оставить знаки равновероятными. Запустить алгоритм. Пошагово пронаблюдать процесс кодирования на макете. Записать кодовые комбинации, значение энтропии и рассчитать среднюю длину кодовых комбинаций. Сравнить с равномерным кодом.

Нажать кнопку “Очистить”.

Провести аналогичные исследования для равновероятных сообщений объема алфавита равного 8. Сделать выводы.

5.3. Исследовать источник дискретных не равновероятных сообщений. Установить объем алфавита равным 5, затем создать поля, в которые записать количество появлений знаков как в домашнем задании. Пошагово пронаблюдать процесс кодирования на макете. Сравнить результаты с выполненным домашним заданием. Сделать выводы.

Установить объем алфавита любым от 10 до 16. Создать поля со случайным количеством появлений знаков нажав кнопку “случайные”. Запустить алгоритм. Зарисовать процесс кодирования и записать значение энтропии. Записать кодовые комбинации, рассчитать среднюю длину кодовых комбинаций, эффективность кодирования и коэффициент сжатия. Сделать выводы о возможности декодирования сообщений.

5.4. Исследовать источник дискретных сообщений с максимальной эффективностью кодирования. Установить объем алфавита равным 6. Установить вероятности знаков равных отрицательным степеням двойки (для этого можно установить количество появлений: 16; 8; 4; 2; 1; 1). Запустить алгоритм. Записать кодовые комбинации и рассчитать среднюю длину кодовых комбинаций. Сравнить ее с энтропией. Сделать выводы.

Описание лабораторного макета

Лабораторная работа выполняется на компьютере с использованием виртуального макета, реализованного в среде Matlab. Структурная схема макета приведена на рис. 2. В состав лабораторного макета входит: источник дискретных сообщений, генератор случайных значений и кодер Хаффмана / Шеннона-Фано. Объем алфавита источника M_A устанавливается в пределах от 2 до 16. Переключатель позволяет устанавливать частоты появлений знаков вручную или с помощью генератора случайных значений. Кодер работает в пошаговом режиме, результат работы которого отображается на дисплее.

 

Рисунок 2 – Структурная схема лабораторного макета

 

Требования к отчету

7.1 Название лабораторной работы.

7.2 Цель работы.

7.3 Результаты выполнения домашнего задания.

7.4 Структурные схемы исследований и результаты выполнения пп. 5.2…5.4 лабораторного задания (построение дерева кодирования Хаффмана / алгоритма Шеннона-Фано, расчеты средней кодовой длины, коэффициента сжатия и т.п.).

7.5 Выводы по каждому из пунктов задания, в которых представить анализ полученных результатов (совпадение теоретических и экспериментальных данных и т.п.).

7.6 Дата, подпись студента, виза преподавателя с оценкой по 100-бальной системе.

Литература

1. Панфилов И.П., Дырда В.Е. Теория электрической связи: Учебник для техникумов – М.:Радио и связь, 1991. – 344с.

2. Стеклов В.К., Беркман Л.Н. Теорія електричного зв’язку; за ред. Стеклова В.К. – К.: Техніка, 2006 – 552с.

3. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. 2-е издание: Пер. с англ. – М.: Издательский дом “Вильямс”, 2003 – 1104с.

Поделиться:

Воспользуйтесь поиском по сайту: