 |
Движение воды в зонах аэрации и насыщения
|
|
|
|
Содержание
Введение
1. Движение воды в зонах аэрации и насыщения
2. Движение подземных вод в водоносных пластах. Определение скорости движения подземных вод
3. Установившееся и неустановившееся движение подземных вод. Методы моделирования фильтрации
4. Приток воды к водозаборным сооружениям
4.1 Приток безнапорных вод в совершенную горизонтальную дрену (канаву)
4.2 Расчет притока грунтовых вод в скважину
4.3 Расчет притока напорных вод в совершенную дрену
4.4 Расчет притока артезианских вод в скважину
5. Методы определения коэффициента фильтрации горных пород. Определение радиуса влияния
Заключение
Список источников литературы
Введение
Гидрогеология — наука, изучающая подземные воды Земли, их историю, происхождение, формирование, состав, режим, геологическую и геохимическую деятельность. Но главной целью гидрогеологических исследований остается выявление новых резервов питьевой воды. В связи с быстрым ростом численности населения нашей планеты проблема запасов природных вод становится особенно острой. В ряде районов уже сейчас испытывается большой недостаток пресной воды, некоторые страны импортируют воду из других государств.
По количеству водных ресурсов Россия занимает одно из первых мест в мире. Однако промышленность и население нашей страны распределены неравномерно, в связи с чем и у нас в отдельных районах возникают очень большие потребности в питьевой воде. Такое положение сложилось в отдельных районах Урала. В РФ, к тому же, есть ряд засушливых районов с отсутствием водных ресурсов или острым их недостатком.
Роль подземных вод в жизни человека, животных и растений исключительно велика, в связи с этим значение гидрогеологии для народного хозяйства переоценить трудно.
|
|
|
Движение воды в зонах аэрации и насыщения
В зоне аэрации, т. е. в толще пород, расположенной между дневной поверхностью и зеркалом грунтовых вод, находятся:
а) водяной пар, заполняющий поры породы;
б) гигроскопическая влага, обусловливающая гигроскопическую влажность пород;
в) пленочная вода, обволакивающая зерна пород в виде пленок различной толщины, и
г) капиллярная вода, располагающаяся в виде капиллярной каймы над зеркалом грунтовых вод.
Движение подземных вод в зоне аэрации может происходить в виде передвижения пара, в виде пленочного движения, свободного просачивания и капиллярного движения.
Движение парообразной и гигроскопической влаги. А. Ф. Лебедевым было экспериментально доказано, что влага в парообразном состоянии передвигается от участка с большей упругостью водяного пара к участку с меньшей его упругостью. Упругость же зависит от температуры и влажности пород. Таким образом, если между различными участками горных пород появляется разница в температуре или влажности, возникает движение водяных паров. При одинаковой температуре движение направлено от более влажных частиц к менее влажным; при одинаковой влажности — от более к менее нагретым. Поэтому летом парообразная влага движется сверху вниз, а зимой — снизу вверх.
Гигроскопическая влага также передвигается в порах пород в виде водяного пара.
Движение воды в пленочном состоянии. По А. Ф. Лебедеву, движение воды в пленочном состоянии происходит под действием молекулярных сил и не подчиняется влиянию силы тяжести.
Рассмотрим движение пленочной воды на примере. Допустим, что мы имеем две одинаковые по диаметру частицы породы, соприкасающиеся между собой. Частица с центром О1 покрыта пленкой воды толщиной Р1, а вторая частица — более тонкой пленкой, толщиной Р2. Рассмотрим влияние частиц породы на частицу воды, расположенную в точке С. Легко убедиться, что расстояние О1С=R+P1 и оно больше, чем О2С=R+P2 т. е. частица 2 будет оказывать большее притяжение на частицу воды в точке С, чем частица породы с центром О1, В результате частица воды С перейдет на пленку, обволакивающую частицу породы 2. Движение частиц воды происходит до тех пор, пока толщина пленок на обеих частицах породы станет одинаковой.
|
|
|
Движение воды в виде просачивания. Просачивание в породах может происходить в виде отдельных струек и в виде сплошной массы воды. В первом случае отдельные струйки воды движутся самостоятельно, разрозненно. Вначале происходит смачивание частиц грунта, после чего под действием сил тяжести избыточная вода в виде гравитационной просачивается вниз.
Такой вид движения Г. Н. Каменский назвал свободным просачиванием. Второй вид движения наблюдается в случае, если породы насыщены водой полностью. Движение воды здесь происходит сверху вниз под действием силы тяжести. Этот вид движения влаги назван инфильтрацией.
Капиллярное движение имеет место как в верхней части зоны аэрации при просачивании и инфильтрации, так и над зеркалом грунтовых вод (в капиллярной зоне). В первом случае капиллярное движение происходит сверху вниз (капиллярное всасывание), во втором — снизу вверх {капиллярное поднятие).
В породах, насыщенных водой, т. е. в зоне насыщения, движение воды может происходить в двух формах:
1) ламинарного, при котором струйки воды текут параллельно, без перемешивания и
2) турбулентного, при котором происходит хаотическое движение частиц жидкости и интенсивное перемешивание ее слоев. Переход от ламинарного движения к турбулентному и обратно происходит при достижении определенной скорости частиц жидкости, называемой критической скоростью. Движение подземных вод в нескальных породах происходит по типу ламинарного.
Чтобы установить закономерности движения жидкости в породах, французский ученый X. Дарси в 1856 г. поставил несложный опыт, который заключался в следующем. В цилиндр, наполненный песком, наливали слой воды, поддерживая ее уровень постоянным. Вода после просачивания через песок выливалась через кран в нижней части цилиндра. В цилиндр были вставлены изогнутые трубки, так называемые пьезометры. Вода в них устанавливалась на различных уровнях (в верхнем пьезометре — выше) в связи с тем, что в процессе фильтрации через поры грунта вода преодолевала сопротивление и на это терялась часть напора.
|
|
|
В результате проведенных исследований Дарси установил, что количество воды, профильтровавшейся через песок в единицу времени (расход, О), прямо пропорционально разности уровней воды в пьезометрических трубках (∆Н=Н2 — Н1), площади поперечного сечения цилиндра (F) и некоторому коэффициенту пропорциональности (К) и обратно пропорционально высоте слоя песка (I). Оказалось, что коэффициент К зависит от свойств песка и его стали называть коэффициентом фильтрации (Кф). Эта зависимость получила название закона Дарен и обычно записывается в следующем виде (1):
 (1)
(1)
Выражение 
обозначают буквой / и называют напорным, градиентом или гидравлическим уклоном. Тогда можно записать
 (2):
(2):
Если разделить обе части уравнения на F, то получим скорость фильтрации (υ) (2):
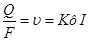 (3):
(3):
Таким образом, скорость фильтрации прямо пропорциональна коэффициенту фильтрации и напорному градиенту. Формула (3) представляет собой уравнение прямой линии, в связи с чем закон Дарси называют линейным законом фильтрации.
Если в выражении (3) принять I=1, что имеет место при уклоне, равном 45°, получим
 (4):
(4):
т. е. коэффициент фильтрации — это та скорость просачивания, которую имел бы поток при уклоне, равном единице.
Не следует при этом смешивать скорость фильтрации со скоростью движения частиц воды. Дело в том, что Дарси при расчетах принимал площадь поперечного сечения потока (F)равной сечению цилиндра, тогда как в действительности вода передвигалась в породе только по порам. Чтобы получить действительную скорость (и)движения подземных вод в порах грунта, необходимо расход воды разделить на площадь поперечного сечения и пористость грунта (n).
 (5):
(5):
|
|
|
Так как
 ,
,
то
 (6):
(6):
Это выражение показывает, что действительная скорость движения подземных вод больше скорости фильтрации, так как величина пористости всегда меньше единицы.
Необходимо заметить, что коэффициент фильтрации выражают в м/сут, хотя в некоторых случаях применяют см/с и км/год.
Если движение подземных вод происходит в крупных пустотах горных пород, то оно становится турбулентным и подчиняется нелинейному закону фильтрации, который выражается уравнением Шези — Краснопольского
 (7):
(7):
Таким образом, скорость фильтрации при турбулентном движении пропорциональна коэффициенту фильтрации и напорному градиенту в степени ½
|
|
|


