Кластеризация данных

Решение задачи общей нелинейной регрессии в системе STATISTICA Neural Networks

http://www.statsoft.ru/statportal/tabID__32/MId__141/ModeID__0/PageID__160/DesktopDefault.aspx

 

Постановка задачи

Рассматривается реальный физический процесс, который, достаточно хорошо описывается пятью переменными в виде z = f (x,y, factor1, factor2), где

z - зависимая переменная, показатель выхода процесса;
x - первая непрерывная независимая переменная;
y - вторая непрерывная независимая переменная;
factor1 - первый независимый фактор, принимающий всего два значения m и s;
factor2 - второй независимый фактор, принимающий всего два значения l и d.

За историю наблюдения за процессом накопился массив данных, которые сохранены в таблице системы STATISTICA. - Рис.1.

 

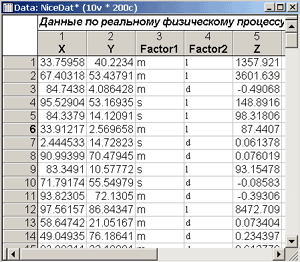
Рис.1. Таблица исходных данных о процессе.

 

Цель исследования - построение математической модели физического процесса на основе исходных данных, которая по заданной четверке значений (x, y, factor1, factor2) выдавала бы отклик z с точностью не хуже 5%.

Нейросетевые алгоритмы хороши, когда:

1. зависимость между переменными есть;
2. зависимость определенно нелинейная;
3. о явном виде зависимости сказать что-либо сложно,

 

Универсальных правил выбора топологии нейронной сети для решения той или иной задачи нет.

Теорема Колмогорова о полноте утверждает, что нейронная сеть способна воспроизвести любую непрерывную функцию.

В 1988 году обобщили теорему Колмогорова и показали, что:

любая непрерывная функция может быть аппроксимирована трехслойной нейронной сетью с одним скрытым слоем и алгоритмом обратного распространения ошибки с любой степенью точности.

 

Поиск нужной конфигурации сети:

· в Модуле Neural Networks системы STATISTICA

· инструмент “ Intelligent Problem Solver”

 

Запуск модуля Neural Networks:

· воспользуемся одноименной командой

· основное меню системы STATISTICA - Statistics.

· Команда Neural Networks

· вызов стартовой панели модуля STATISTICA Neural Networks (SNN).

Разделы.

Раздел Problem Types.

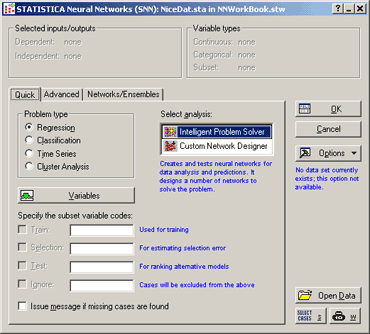
Рис.3. Стартовая панель модуля SNN.

 

· Во вкладке Quick - Быстрый доступны три, наиболее часто используемые опции.

· В разделе Problem Type - Класс задач – выбрать класс задач.

· Построение многомерной з ависимости – это построение многомерной регрессии =>

 

· Класс задач следует указать Regression - Регрессия.

 

доступны классы задач:

· Regression - Регрессия

· Classification – Классификация

· Time series - Прогнозирование временных рядов

· Cluster analysis - Кластерный анализ.

 

Указать переменные для проведения Анализа:

· кнопка Variables =>

· появляется диалоговое окно Select input (independent), output (dependent) and selector variables =- Укажите входные (независимые), выходные (зависимые) и группирующие переменные.

 

Задать три списка переменных:

· Continuous outputs - Непрерывные выходящие, в нашем случае, - это переменная z.

· Continuous inputs - Непрерывные входящие, в нашем примере, - это переменные x и y.

· Categorical inputs - Категориальные входящие, у нас это переменные Factor1 и Factor2.

Раздел Subset variable - Разбиение на подмножества:

· н еобязателен для заполнения

· служит для выбора переменной, в которой содержатся коды для разбиения данных на:

ü обучающее

ü контрольное

ü тестовое множества.

 

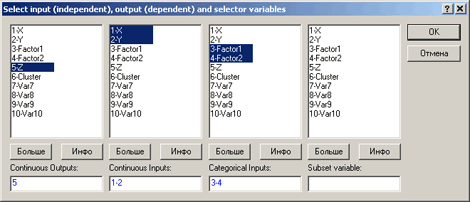
Рис.4. Выбор переменных для Анализа.

 

Раздел Select analysis - Выбор анализ:

доступны 2 опции:

· Intelligent Problem Solver - нам требуется, устанавливается по умолчанию

· Custom Network Designer

Нажмем кнопку OK.

 

Появляется окно настройки процедуры Intelligent Problem Solver:

· окно содержит большое количество опций, распределенных в различных вкладках

· нам понадобится вкладка Quick - Быстрый и её раздел Optimization Time - Время оптимизации (содержит группу опций, отвечающих за время исполнения алгоритма поиска нейронной сети)

· 2 возможности:

1)задать количество сетей, которые необходимо протестировать (подходят ли они для решения задачи);

вручную задать время выполнения алгоритма. Для этого необходимо воспользоваться опцией Hours/Minutes - Часы/Минуты.

 

Воспользуемся 1-й опцией. В разделе Optimization Time - Время оптимизации в разделе Networks tested - Количество тестируемых сетей укажем 100.

Рис.5. Задание количества тестируемых сетей.

 

Для запуска процедуры поиска сетей нажмем ОК.

Состояние алгоритма поиска отображается в диалоговом окне IPS Training In Progress - Процесс поиска сети, см. Рис.6.

 

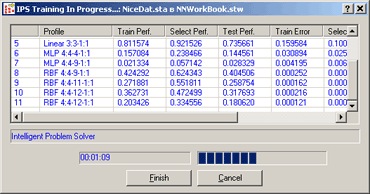
Рис.6. Процесс поиска сети.

 

· информация о времени исполнения алгоритма

· о рассмотренных нейронных сетях

 

Цель алгоритма поиска:

· перебор ряда нейросетевых конфигураций

· выбор наилучшей с точки зрения:

ü минимума ошибки на выходе сети и

ü максимума её производительности

 

Сети необходимо:

· Обучать

· рассчитывать их ошибки и производительности

· эти показатели сравнивать

 

Каждая нейронная конфигурация описывается строкой в информационном поле диалогового окна. Показатели:

· Profile - Тип сети

· Train (Select, Test) Performance - Производительность сети на обучающем (контрольном, тестовом) множестве

· rain Error - Ошибка обучения.

 

Раздел Profile - Тип сети описывает:

· топология нейронной сети = её класс (персептрон, сеть RBF и т.д.)

· количество входных и выходных переменных

· количество скрытых слоев

· число элементов на каждом скрытом слое.

 

Алгоритм поиска сети разбивает (по умолчанию) все множество наблюдений на:

· Training – Обучающее

· Selection – Контрольное:

· Test - Тестовое

 

Training – Обучающее - обучение сети = изменение весовых коэф. каждого из нейронов пропорционально ошибке на выходе

Selection – Контрольное:

контрольное множество в процедуре изменения весов нейронов не участвует

служит для кросс – проверки - контроля способности сети к обобщению данных, на которых она не обучалась

 

На каждом шаге алгоритма обучения:

· рассчитывается ошибка для всего набора наблюдений из контрольного множества

· сравнивается с ошибкой на обучающем множестве

· Как правило, ошибка на контрольном множестве превышает ошибку на обучающем множестве, так как:

· алгоритм обучения нацелен на минимизацию ошибки на выходе сети

 

Если наблюдается рост ошибки на контрольном множестве и её уменьшение на обучающем множестве:

· сеть "зазубрила" предъявленные ей наблюдения

· не способна к обобщению

· такое состояние называется переобучением - переобучения надо избегать.

Алгоритм Intelligent Problem Solver:

· самостоятельно отслеживает переобучение

· при завершении обучения возвращает сеть в наилучшее состояние (Retain Best Network - Восстановить наилучшую сеть).

Test - Тестовое множества:

· не участвует в обучении вообще

· после завершения обучения исп-ся для:

ü расчета производительности полученной сети

ü её ошибки на данных, о которых "ей вообще ничего неизвестно".

 

Хорошая сеть:

· ошибка одинаково мала на всех трех подмножествах.

 

Производительность сети в задаче регрессии – это:

· отношениестандартного отклонения ошибок сети к стандартному отклонению исходных данных (SD-ratio).

· Эмпирическое правило гласит, что если SD-ratio не превышает значения 0.2, сеть подобрана хорошо.

· Производительность рассчитывается для каждого из трех подмножеств

· разброс значений производительности на каждом из подмножеств д.б. небольшим.

 

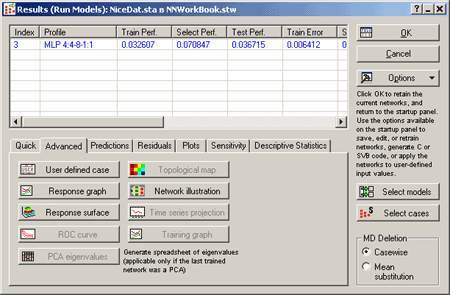
Рис.7. Диалоговое окно результатов поиска сети.

 

Итог:

· отобрана сеть - трехслойный персептрон

· 8 нейронов на скрытом слое

· производительностью 0.07.

 

Выбор нужной сети из списка, предлагаемого Intelligent Problem Solver:

· окно Results - Результаты

· кнопка Select Models - Выбрать модели

· В появившемся диалоговом окне подсветить нужную нейронную сеть

· нажать ОК

 

Посмотреть иллюстрацию выбранной сети:

· Вкладка Advanced - Дополнительно диалогового окна результатов.

· кнопка Network Illustration

 

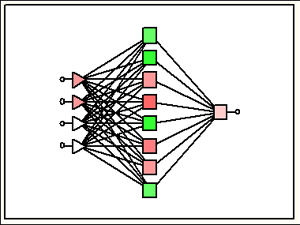
Рис.8. Иллюстрация выбранной нейронной сети.

 

Построить график зависимости наблюдаемых значений выходной переменной z от предсказанных значений – отражает качество работы нейронной сети:

· вкладка Plots – Графики

· кнопка Graph X versus Y - График X от Y

· предварительно указав в качестве X - axis - Observed - Наблюдаемые, Y - axis - Predicted - Предсказанные.

Рис.9. График зависимости предсказанных значений Z от наблюдаемых Z.

 

Для хорошей модели:

· точки этого графика должны располагаться как можно ближе к прямой, лежащей под углом 45 градусов к осям координат.

· На первый взгляд, так оно и происходит.

Рассмотрим численные результаты:

· Вкладка Predictions - Прогнозы диалогового окна результатов

· кнопка Predictions - Прогнозы для просмотра результатов работы нейронной сети на всем наборе данных

· =>(см. Рис.10) - не все так хорошо, как хотелось бы:

 

Рис.10. Таблица результатов прогона всего набора данных через нейронную сеть.

 

· нулевые значения z - ошибки колоссальны

· значения z, не превышающие 100 - результаты сильно противоречивы

· большие значения z порядка 1000 – рез-ты хорошие

Итог:

требуемой погрешности 5% на всех данных достичь не удалось.

 

Причины заблуждения:

· Значения переменной z изменяются от 0 до 10000

· При расчете статистик производительности основную роль сыграли именно "большие" данные

· кричащая ошибка в области малых чисел была утеряна в результате усреднения всех ошибок.

 

Более точно посмотреть график:

· воспользуемся опцией Zoom – Увеличить - расположена на графич. панели инструментов (панель видна при активном графическом документе STATISTICA) в области малых значений z на графике (см. Рис.11).

 

 

Рис.11. График зависимости предсказанных значений Z от наблюдаемых Z в области малых значений Z.

 

· Отчетливо видно отсутствие какой-либо зависимости между наблюдаемыми и предсказанными значениями.

· имеются основания полагать, что функция изучаемого физического процесса не является непрерывной =>

· получили противоречащий теореме Колмогорова о полноте результат

· в некоторых областях пространства независимых переменных функция процесса ведет себя непрерывно (область больших значения z)

· желательно такие области локализовать

· Для этого осуществим разбиение данных на однородные группы, или проведем кластеризацию.

 

Кластеризация данных

Сформулируем задачу кластерного анализа:

· имеется 200 объектов (по количество доступных для построения моделей наблюдений) в 4х-мерном пространстве (x, y, factor1, factor2).

· переменную z мы отбросили (она зависит от всех остальных и заведомо не повлияет на качество кластеризации) Необходимо разбить эти объекты на ряд групп, таким образом:

1. внутри группы объекты максимально схожи между собой;
2. группы максимально между собой различаются.

 

· скорее всего, ввиду однородности, внутри каждого кластера зависимость z = f(x, y, factor1, factor2) будет непрерывной функцией

· построив для каждого из кластеров отдельную нейронную сеть, мы построим модель физического процесса.

 

Сравнение объектов.

· в рассматриваемом пространстве (x, y, factor1, factor2) ввести количеств. меру сходства между объектами

· кажется удобным введение евклидова расстояния - корень из суммы квадратов покоординатных разностей

Но различные независимые переменные могут измеряться в разных шкалах с различными диапазонами:

· значения одной переменной измеряются в сотнях и изменяются в пределах десяти

· другая переменная в среднем равна нулю и изменяется в пределах единицы =>

· вклад последней в евклидово расстояние будет пренебрежительно малым =>

· Нужна процедура стандартизации переменных - приведение всех переменных к единой шкале:

 

Стандартизация:

· данные изменяются в пределах нуля в диапазоне ±3

· большая часть всех значений будет принадлеж. интервалу (-1, 1)

· процедура стандартизации не изменяет структуру взаимодействий между переменными =>

· стандартизация не влияет на структуру кластеров

· стандартизация применима к переменным, измеряемым в непрерывной шкале

 

Cтандартизация непрерывной переменной:

· необходимо выделить соответствующий столбец

· нажать правую кнопку мыши

· из появившегося контекстного меню выбрать раздел Fill/Standardize Block - Заполнить/Стандартизовать Блок

· выполнить команду меню Standardize Columns - Стандартизовать столбцы

 

=>Эту процедуру необходимо выполнить для переменных x и y.

 

Стандартизация категориальных переменных:

· Переменная factor1 принимает значения только (s, m)

· переменная factor2 - значения (l, d)

· По умолчанию система STATISTICA уровням факторов этих переменных присвоила значения (101, 102)

· надо перекодировать, чтобы диапазон их изменения соответствовал диапазону изменения непрерывных переменных

 

Перекодировка каждой категориальной переменной:

· дважды кликнуть на ее названии в Таблице данных

· в появившемся диалоговом окне спецификаций переменных нажать кнопку Text Labels - Текстовые метки.

 

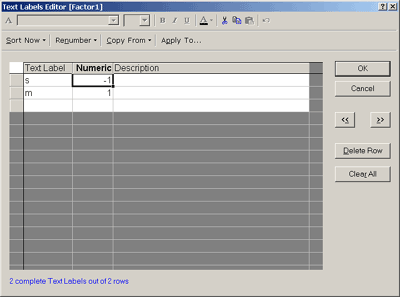
Рис.12. Изменение значений уровней факторов категориальной переменной.

 

· В разделе Numeric - Число диалогового окна Text Labels Editor - Редактор текстовых меток необходимо поставить значения -1 и 1 =>

· среднее категориальных переменных равно нулю

· диапазон значений сравним с диапазоном изменения непрерывных переменных

 

Замечание:

· округленный до целых результат формальной стандартизации категор. переменных приводит к тому же результату

· Но если просто выполнить стандартизацию категор. переменных, текстовые значения будут утеряны, что может привести к некорректным результатам.

 

Число кластеров:

· Эксперты, имеющие представление о природе процесса, могут предположительно указать на число кластеров

· существует агломеративный метод иерархической классификации, или иерархический кластерный анализ

Иерархический кластерный анализ:

· на первом шаге каждый объект выборки рассматривается как отдельный кластер

· Процесс объединения происходит последовательно:

· на основании матрицы расстояний объединяются наиболее близкие объекты

· Если матрица сходства первоначально имеет размерность mxm, то полностью процесс кластеризации завершается за m-1 шагов =>

· в итоге все объекты будут объединены в один кластер

 

Последоват-ть объединения м.б. представлена в виде графа - дерева (дендрограммы):

· На оси абсцисс - имена наблюдений

· по оси ординат, - расстояние объединения наблюдений в кластеры

· чем выше расположена ветвь дерева на дендрограмме, тем позднее было проведено объединение объектов.

 

Проведем иерархический кластерный анализ на стандартизованных данных:

· команды меню Statistics - Multivariate Exploratory Techniques - Cluster Analysis - Анализ - Многомерный разведочный анализ - Кластерный анализ

· В появившемся окне Clustering method - Методы кластеризации выберем Joining (tree clustering) - Иерархическая классификация

· нажмем ОК

· В окне Cluster Analysis: Joining (Tree Clustering) - Кластерный анализ: иерархическая классификация выберем вкладку Advanced – Дополнительно

· В качестве переменных для анализа выберем x, y, Factor1, Factor2

· В разделе Cluster - Объекты выберем Cases (Rows) - Наблюдения (строки)

· В качестве меры сходства в разделе Distance measure - Мера близости укажем Euclidian distances - Евклидово расстояние

· Остальные параметры оставим по умолчанию

· Вид диалогового окна со всеми нужными установками представлен на Рис.13.

 

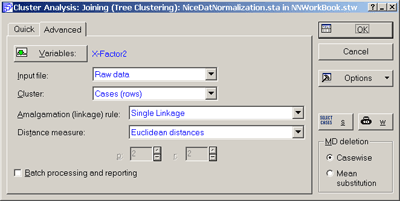
Рис.13. Диалоговое окно задания параметров иерархической классификации.

 

· Нажмём ОК:

В появившемся окне результатов объединения:

· отменим опцию Rectangular Branches - Прямоугольные ветви и

· нажмем кнопку Vertical icicle plot - Вертикальная дендрограмма

· Результат построения графика - Рис.14.

 

Рис.14. Вертикальная дендрограмма древовидной классификации для переменных x, y, factor1, factor2.

 

древовидная диаграмма:

· отображает историю объединения объектов в кластеры

· Чем выше ветви дерева - графа, тем позднее объекты были объединены

· на Рис.14 отчетливо выделяются 4 ветви дерева, объединенные на одинаковой высоте

· Каждая из этих ветвей имеет продолжение в виде скоплений ветвей меньшей высоты – кучностей

· структура скоплений не обладает ярко выраженной иерархией.

· можно утверждать, что все множество данных хорошо разделяется на 4 кластера

· график показывает: однородность данных внутри кластера и максим. отдаленность самих кластеров достигнуты

 

Выявление переменных, "ответственных" за кластеризацию.

· Чем меньше переменных ответственны за разбиения данных на кластеры, тем легче понять физический разбиения. Проведем иерархическую классификацию для переменных всех переменных, кроме x

· Последовательность действий аналогична предыдущему анализу

· Результат кластеризации приведен в виде дендрограммы на Рис.15.

 

4

Рис.15. Вертикальная дендрограмма древовидной классификации для переменных y, factor1, factor2.

 

· Высота больших ветвей диаграммы осталась прежней ->расстояния между кластерами остались прежними.

· высоты скоплений ветвей уменьшились ->внутриклассовые различия стали значительно меньше =>

· в отсутствие переменной x получена более качественная кластеризация

 

Теперь необходимо разбить объекты по кластерам:

воспользуемся итеративной процедурой, методом к-средних

· процесс классификации начинается с задания начальных условий:

ü количество образуемых кластеров

ü центры этих кластеров

· каждое многомерное наблюдение совокупности относится к тому кластеру, центр которого ближе всех к этому наблюдению

· Затем выполняется проверка на устойчивость классификации

· Если классификация устойчива, процесс останавливается. В противном случае, происходит очередная процедура разбиения объектов по кластерам.

 

Выполним метод K-средних на стандартизованных данных:

· воспользуемся командами меню Statistics - Multivariate Exploratory Techniques - Cluster Analysis - Анализ - Многомерный разведочный анализ - Кластерный анализ

· В окне Clustering method - Методы кластеризации выберем К-means clustering - Кластеризация методом К-средних

· нажмем ОК

· В окне Cluster Analysis: К-means clustering - Кластерный анализ: кластеризация методом К-средних выберем вкладку Advanced – Дополнительно

· В качестве переменных для анализа выберем y, Factor1, Factor2

· В разделе Cluster - Объекты выберем Cases (Rows) - Наблюдения (строки)

· В поле Number of Clusters - Число кластеров введем 4

· Вид диалогового окна со всеми нужными установками представлен на Рис.16.

· нажмем ОК

· Вкладка Advanced - Дополнительно окна результатов - кнопка Save classifications and distances - Сохранить результаты классификации и расстояния

· В появившейся Таблице результатов скопируем переменную Cluster и добавим ее в исходный файл данных (Добавление переменных: дважды щёлкнуть мышью на пустой клетке строки названий переменных – окно - указать название)

· В строках данной переменной содержатся номера кластеров, к которым были отнесены многомерные объекты.

 

Кластеризация проведена.

 

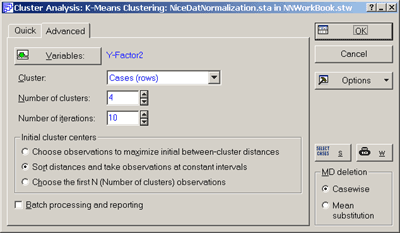
Рис.16. Диалоговое окно задания параметров кластеризации методом K-средних.

 

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: