Совместное действие изгиба и кручения

Задача № 5

Вариант 0

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ

Исходные данные:

L=15 м, z₁=0 м, z₂=9 м, z_p1=4 м, z_p2=15 м, z_qH=0 м, z_qK=7 м, P₁=-30 кН, P₂=50 кН, q=-20 кН/м, m=-20 кНм, J_пр/J_л=1

Расчетная схема:

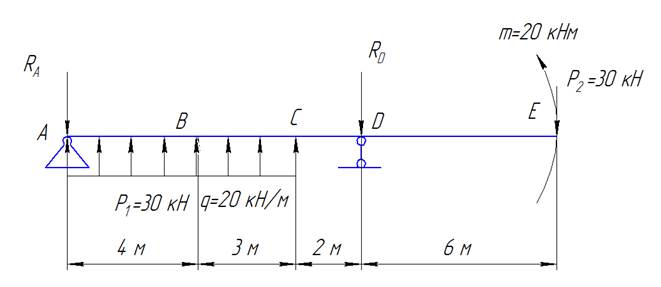
Определяем опорные реакции. Для этого составим два уравнения равновесия:

Проверка

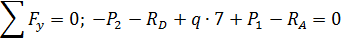
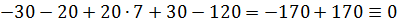
Реакции определены верно

разделим ось балки на участки

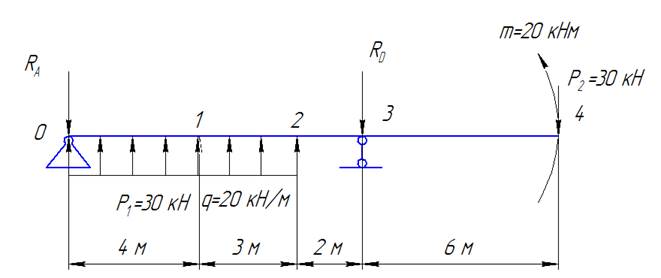
построим эпюру изгибающих моментов от заданной нагрузки

Для участка 0-1:

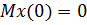
Для участка 1-2:

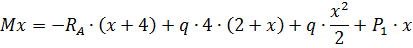
Точка экстремума

Минимальный момент:

Для участка 4-3:

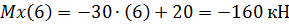
Для участка 2-3:

Эпюра имеет вид

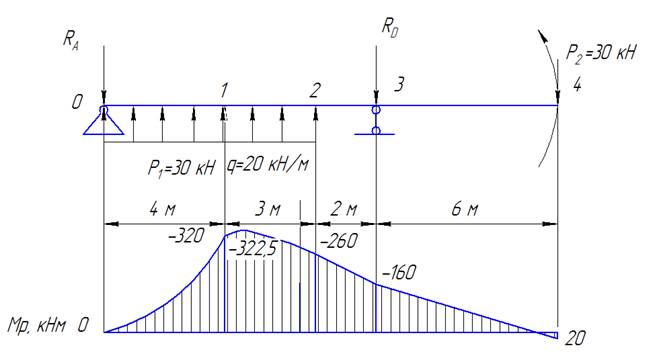
Прикладываем в сечение Z_{Р 2} единичную нагрузку и строим эпюру моментов

Реакции опор составляют:

Эпюра моментов имеет вид:

Прикладываем в сечение Z_{Р 2} единичный момент и строим эпюру моментов

Эпюра моментов имеет вид:

 

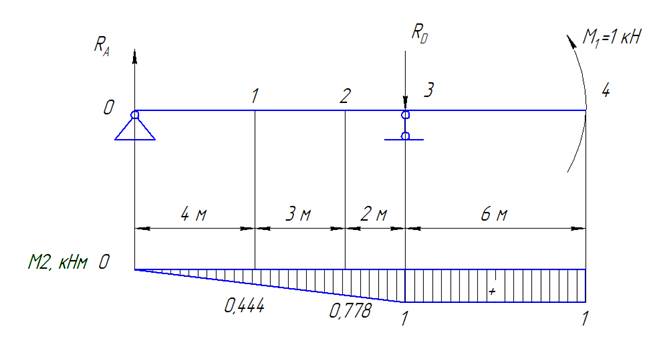
Вектор прив. перемещений

- 4977,44395

-1864,513327

Вектор действит. перемещений

-1,352566291

-0,50666123

Задача № 6

Вариант 0

СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ

Пространственный консольный брус с ломаным очертанием осевой линии нагружен сосредоточенной силой F =1 кН или равномерно распределенной нагрузкой q =1 кН/м. Вертикальные элементы бруса имеют круглое поперечное сечение диаметром d=0,068 , горизонтальные элементы - прямоугольное сечение (b×c). Ширина сечения b = d +20 мм=0,088 м, а высота сечения с = 0,5 b=0,044 м. а=1,9 м

Требуется:

1. Построить в аксонометрии шесть эпюр: M_x, M_y, M_z, Q_x, Q_y, N_z;

2. Указать вид сопротивления для каждого участка бруса;

3. Определить на каждом участке нормальные напряжения от совокупности внутренних усилий N_z, M_x, M_y и касательные напряжения от крутящего момента M_z (напряжениями от Q_x и Q_y можно пренебречь);

4. Найти расчетное напряжение по III теории прочности на участке, где возникают одновременно нормальные и касательные напряжения.

Расчетная схема

1. Построить в аксонометрии эпюры Mx, My, Mz, Nz, Qx, Qy. Заметим, что так как заданная система пространственная, при произвольном характере нагружения, в опорном сечении, где установлена заделка, возникает шесть опорных реакций (три опорные силы и три момента). Для определения опорных реакций, в данном случае, можем применить шесть уравнений равновесия статики. Так как число независимых уравнений равновесия равно числу опорных реакций, то можно сделать вывод, что рассматриваемая система в виде ломаного бруса, с заделанным одним концом, является статически определимой. Поэтому рассматриваемая система разрешима по методу сечений. Далее, учитывая особенности конструкции, определение величин внутренних усилий можно осуществить без предварительного вычисления величин опорных реакций.

Брус имеет три участка АВ, ВС и СD. При этом, после рассечения бруса на две части будем рассматривать равновесие оставшейся части, не связанной с заделкой (чтобы избежать предварительного определения опорных реакций в заделке бруса). Внутренние силовые факторы можно рассматривать как реакции, действующие в сечении на оставшуюся часть со стороны отброшенной части, поэтому процесс определения шести величин Mx, My, Mz, Nz, Qx, Qy может быть сведен к известному процессу определения опорных реакций.

Участок АВ

Участок ВC

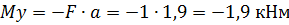
Участок CD

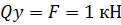
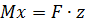
Эпюры показаны на рисунке ниже

2. Установить вид сопротивления для каждого участка бруса. По эпюрам устанавливаем вид сопротивления на каждом участке бруса. На участке АВ возникают изгибающий момент My и поперечная сила Qx, что свидетельствует о наличии поперечного изгиба. На участке ВС возникает изгибающий момент My, продольная сила N, что свидетельствует о наличии поперечного изгиба с растяжением. На участке СD действуют изгибающий момент Mx, крутящий момент Mz, поперечная сила Qy, что свидетельствует о наличии косого изгиба.

3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N, M_x,M_y и M_z (касательными напряжениями от Q_x и Q_y можно пренебречь).Участок АВ. Наибольшая величина изгибающего момента M_y,судя по эпюре возникает в сечении, бесконечно близком к точке В. Максимальные нормаль­ные напряжения при изгибе определяются по формуле:

Участок ВС. По эпюрам M_y и Nz устанавливаем, что опасным является сечение, бесконечно близкое к точке С.

При действии растягивающей силы N во всех точках поперечного сече­ния возникают одинаковые нормальные напряжения:

Участок СD. По эпюрам M_x, M_y M_z видим, что равными по опасности будут сечения, бесконечно близкое к D

При кручении сечения возникают касательные на­пряжения, максимальные значения которых определяются по фор­муле:

гдеW_p - момент сопротивления при кручении. Известно, что

W_p = b×c³ = 0,493×0,044³ = 42×10^-6 м³,

Здесьb - коэффициент,зависящий от от­ношения большей стороны прямоугольника к меньшей (в данном случае при b/c= 2, b = 0,493).

Тогда

4. Проверка прочности при расчетным сопротивле­нииR = 180 МПа.Расчетное напряжение по третьей теории прочности для плоского напряженного состояния определяется по формуле:

Нормальные и касательные напряжения возникают на участке CD

Проверка прочности по третьей теории:

Задача № 7

ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЕЙ

Вариант 0

Для стойки двутаврового поперечного сечения (ГОСТ 8239-72), одинаково закрепленной в обеих плоскостях потери устойчивости и центрально сжатой силой F по заданной схеме требуется:

1. Определить грузоподъемность F указать положительные и отрицательные стороны конструкции колонны из двутавра;

2. Для найденной грузоподъемности F, в целях лучшего использования материала, заменить двутавр более рациональным сечением из двух двутавров или двух швеллеров, соединенных планками на сварке, подобрать для нового варианта сечение, сравнить его по площади с первоначальным и вычертить в масштабе с указанием числовых размеров. Расчетное сопротивление материала R = 190 МПа.

Исходные данные

l=3,6 м, Номер двутавра по ГОСТ 8239-72 -30,

Расчетная схема

1. Расчет на устойчивость стойки из двутавра. Из сортамента ГОСТ 8239-72выписываем необходимые дан­ные для двутавра №30: A = 46,5×10^-4 м²;i_x = 0,123 м;i_y = 0,0269 м.

Тогда имеем:

Для нахождения величины нужно знать максимальную гиб­кость стойки, которая определится из формулы

 

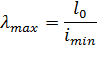
гдеl₀ - приведенная(свободная) длина стойки, l₀ = m*l.Здесь m -коэффициент приведенной длины, зависящий от способа закрепле­ния концов стойки (для нашего примера m = 0,7),l - длина стойки; i_min - минимальный радиус инерции сечения стойки (в данном слу­чае - радиус инерции относительно оси y).Таким образом,

 

находим при = 93,7,интерполируя до третьего знака после запятой:

при = 90 = 0,69;

при = 100 = 0,6.

Поэтому при = 93,7

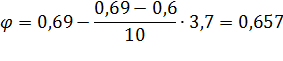
Подставляя значения A, и R в формулу, получим допус­тимое значение сжимающей силы с точки зрения устойчивости рассматриваемой стойки:

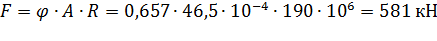
Преимуществом стойки из двутавра является простота конст­рукции и малая трудоемкость изготовления и монтажа, недостат­ком - неравная устойчивость в разных плоскостях.

2. Подбор сечения стойки из двух швеллеров. При рассмотрении этого вопроса составное сечение стойки следует рас­сматривать как цельное, и поэтому расчет приведенной гибкости можно не выполнять. Подбор составного сечения стойки будем производить путем последовательного приближения. Для этого за­даемся произвольным значением , подбираем сечение и сопостав­ляем возникающие в нем напряжения с расчетным сопротивлени­ем. Эта операция производится до тех пор, пока напряжение, возникающее в стойке, будет достаточно близким к расчетному сопротивлению(отклонение не должно превышать ±5%).

Примем = 0,6. Определим требуемую площадь А сечения двух швеллеров:

По ГОСТ 8240-72принимаем швеллер № 22, для которого

Для обеспечения равноустойчивости стойки из двух швеллеров нужно, чтобы гибкость ее была примерно одинаковой в обеих плоскостях. Для принятого сечения из двух швеллеров определим максималь­ную гибкость:

 

находим значение jдля полученной гибкости:

при = 100 = 0,6;

при = 110 = 0,52.

Поэтому при =

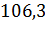
Определяем напряжение в стойке:

Перегрузка составляет

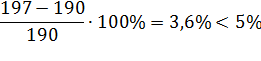
Перегрузка составляет 3,6%,что допустимо.

Окончательно принимаем стойку из двух швеллеров №22.Из сортамента ГОСТ 8240-72выписываем необходимые данные:

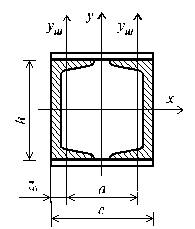
I_x = 2110×10^-8 м⁴,I_y =151 ×10^-8 м⁴,z₀ = 0,0221 м,h = 0,22 м,b = 0,082 м.

Момент инерции поперечного сечения стойки из двух швелле­ров относительно оси x: Момент инерции составного сечения относительно оси yможно изменять, сближая или удаляя швеллеры один относительно другого. Определим расстояние между швел­лерами из условия, что I_y = 1,2×I_x. Имеем с = а +2×z₀ ,где а - расстояние между собственными осями yкаждого из швеллеров. Тогда:

Отсюда

Монтажное расстояние между швеллерами будет с = а + 2×z₀ = = 0,1933 + 2×0,0221 = 0,2375 м, принимаем c = 0,238 м. Сравнивая сечение из двух швеллеров с заданным двутавровым, видим, что площадь заданного сечения составляет 46,5×10^-4 м²,а полученного из двух швеллеров - 41,4×10^-4 м².Таким образом, расход металла на стойку из двутавра (без учета металла на соединительные планки) будет меньше в 50,1/ 46,5 = 1,08 раза, или на 8%,чем на стойку из двух швеллеров.

Однако конструкция стойки из двух швеллеров трудоемка в изготовлении по сравнению со стойкой из двутавра.

Чертеж сечения из двух швеллеров №22

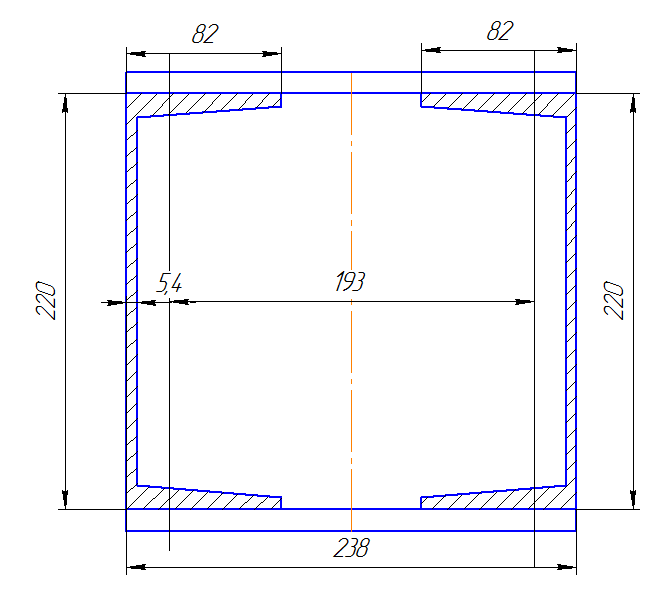
Поделиться:

Воспользуйтесь поиском по сайту: