 |
Обучение решению задач на смекалку (головоломки)
|
|
|
|
Из всего многообразия головоломок наиболее приемлемы в старшем дошкольном возрасте(5-7 лет) головоломки с палочками (можно использовать спички без серы). Их называют задачами на смекалку геометрического характера, так как в ходе решения, как правило, идет трансфигурация, преобразование одних фигур в другие, а не только изменение их количества. В дошкольном возрасте используются самые простые головоломки. Для организации работы с детьми необходимо иметь наборы обычных счетных палочек для составления из них наглядно представленных задач-головоломок. Кроме этого, потребуются таблицы с графически изображенными на них фигурами, которые подлежат преобразованию. На обратной стороне таблиц указывается, какое преобразование надо проделать и какая фигура должна получиться в результате.
Задачи на смекалку различны по степени сложности, характеру преобразования (трансфигурации). Их нельзя решать каким-либо усвоенным ранее способом. В ходе решения каждой новой задачи ребенок включается в активный поиск пути решения, стремясь при этом к конечной цели, требуемому видоизменению или построению пространственной фигуры.
Для детей 5-7 лет задачи на смекалку можно объединить в 3 группы (по способу перестроения фигур, степени сложности).
Задачи на составление заданной фигуры из определенного количества палочек: составить 2 равных квадрата из 7 палочек, 2 равных треугольника из 5 палочек.
Задачи на изменение фигур, для решения которых надо убрать указанное количество палочек.
Задачи на смекалку, решение которых состоит в перекладывании палочек с целью видоизменения, преобразования заданной фигуры.
В ходе обучения способам решения, задачи на смекалку даются в указанной последовательности, начиная с более простых, с тем чтобы усвоенные детьми умения и навыки готовили ребят к более сложным действиям. Организуя эту работу, воспитатель ставит цель - учить детей приемам самостоятельного поиска решения задач, не предлагая никаких готовых приемов, способов, образцов решения.
|
|
|
К такому самостоятельному поиску решения самых простых задач первой группы дети подготовлены в результате повседневной работы. Для этого достаточно дополнительно поупражнять их в составлении геометрических фигур (квадратов, прямоугольников, треугольников) из счетных палочек.
Составление геометрических фигур
(подготовительные игровые упражнения для детей 5 лет)
Цель. Упражнять детей в составлении геометрических фигур на плоскости стола, анализе и обследовании их зрительно-осязательным способом.
Материал: счетные палочки длиной 5 см (15-20 штук на ребенка), 2 толстые нитки длиной 25-30 см.
Ход работы. Воспитатель предлагает детям назвать известные им геометрические фигуры. После перечисления сообщает цель: "Будем составлять фигуры на столе и рассказывать о них". Дает задания:
1. Составить квадрат и треугольник маленького размера.
Вопросы для анализа: "Сколько палочек потребовалось для составления квадрата? Треугольника? Почему? Покажите стороны, углы, вершины фигур".
2. Составить маленький и большой квадраты.
Вопросы для анализа: "Из скольких палочек составлена каждая сторона большого квадрата? Весь квадрат? Почему левая, правая, верхняя и нижняя стороны квадрата составлены из одного и того же количества палочек?"
Можно дать задание на составление большого и маленького треугольника. Анализ выполнения задания проводится аналогично.
3. Составить прямоугольник, верхняя и нижняя стороны которого будут равны 3 палочкам, а левая и правая -2.
|
|
|
После анализа детям предлагают составить любой четырехугольник и доказать правильность выполнения задания.
4. Составить из ниток последовательно фигуры: круг и овал, большие и маленькие квадраты, треугольники, прямоугольники и четырехугольники. Маленькие фигуры составляются из нитки, сложенной вдвое.
Анализ фигур проводится по схеме: "Сравните и скажите, чем отличаются, чем похожи фигуры. Докажите, что фигура составлена правильно".
Уточнение представлений детей о геометрических фигурах; их элементарных свойствах (количество углов и сторон), упражнение в составлении будут способствовать усвоению детьми способов решения головоломок первой группы. Их предлагают детям в определенной последовательности:
Составить 2 равных треугольника из 5 палочек.
Составить 2 равных квадрата из 7 палочек.
Составить 3 равных треугольника из 7 палочек.
Составить 4 равных треугольника из 9 палочек.
Составить 3 равных квадрата из 10 палочек.
Из 5 палочек составить квадрат и 2 равных треугольника.
Из 9 палочек составить квадрат и 4 треугольника.
Из 10 палочек составить 2 квадрата: большой и маленький (маленький квадрат составляется из 2 палочек внутри большого).
Из 9 палочек составить 5 треугольников (4 маленьких треугольника, полученных в результате при-строения, образуют 1 большой).
Из 9 палочек составить 2 квадрата и 4 равных треугольника (из 7 палочек составляют 2 квадрата и делят на треугольники 2 палочками).
Для того чтобы решить эти задачи, нужно владеть способом при-строения, присоединения одной фигуры к другой. Впервые получив такое задание, дети пытаются составить 2 отдельных треугольника, квадрата. После ряда безуспешных попыток догадываются о необходимости пристроения к одному треугольнику, квадрату другого, для чего достаточно 2, 3 палочек.
По мере накопления детьми опыта в решении подобных задач методом "проб и ошибок" количество неправильных проб, практических действий начинает сокращаться. Исходя из этого, воспитатель, сохраняя занимательность, игровой характер упражнений, направляет ребят на целенаправленные пробы, которым предшествует хотя бы элементарное обдумывание конкретного хода решения. В процессе поиска решения обращает внимание ребят на то, что, прежде чем составлять ответ, надо подумать, как это можно сделать. Достаточно провести 3-4 занятия, в процессе которых дети овладевают способами пристроения к одной фигуре другой так, чтобы одна или несколько сторон оказались общими.
|
|
|
Примеры (для детей 5-6 лет)
(Здесь и далее дается методика проведения части занятия с использованием занимательного материала)
Составление фигур из треугольников и квадратов
1. Пример
Цель. Учить детей составлять геометрические фигуры из определенного количества палочек, пользуясь приемом пристроения к одной фигуре, взятой за основу, другой.
Материал: У детей на столах счетные палочки, доска, мел на данном и следующем занятиях.
Ход работы. 1. Воспитатель предлагает детям отсчитать по 5 палочек, проверить и положить их перед собой. Затем говорит: "Скажите, сколько потребуется палочек, чтобы составить треугольник, каждая сторона которого будет равна одной палочке. Сколько потребуется палочек для составления двух таких треугольников? У вас только 5 палочек, но из них надо составить тоже 2 равных треугольника. Подумайте, как это можно сделать, и составляйте".
После того как большинство детей выполнят задание, воспитатель просит их рассказать, как надо составить 2 равных треугольника из 5 палочек. Обращает внимание ребят на то, что выполнять задание можно по-разному. Способы выполнения надо зарисовать. При объяснении пользоваться выражением "пристроил к одному треугольнику другой снизу" (слева и т.д.), а в объяснении решения задачи пользоваться также выражением "пристроил к одному треугольнику другой, используя лишь 2 палочки".
2. Составить 2 равных квадрата из 7 палочек (воспитатель предварительно уточняет, какую геометрическую фигуру можно составить из 4 палочек). Дает задание: отсчитать 7 палочек и подумать, как из них составить на столе 2 равных квадрата.
После выполнения задания рассматривают разные способы пристроения к одному квадрату другого, воспитатель зарисовывает их на доске.
|
|
|
Вопросы для анализа: "Как составил 2 равных квадрата из 7 палочек? Что сделал сначала, что потом? Из скольких палочек составил 1 квадрат? Из скольких палочек пристроил к нему второй квадрат? Сколько потребовалось палочек для составления 2 равных квадратов?"
2. Пример
Цель. Составлять фигуры путем пристроения. Видеть и показывать при этом новую, полученную в результате составления фигуру; пользоваться выражением: "пристроил к одной фигуре другую", обдумывать практические действия.
Ход работы. Воспитатель предлагает детям вспомнить, какие фигуры они составляли, пользуясь приемом пристроения. Сообщает, чем они сегодня будут заниматься - учиться составлять новые, более сложные фигуры. Дает задания:
1. Отсчитать 7 палочек и подумать, как можно из них составить 3 равных треугольника.
После выполнения задания воспитатель предлагает всем детям составить 3 треугольника в ряд так, чтобы получилась новая фигура - четырехугольник (рис. 2). Этот вариант решения дети зарисовывают мелом на доске. Воспитатель просит показать 3 отдельных треугольника, четырехугольник и треугольник (2 фигуры), четырехугольник.

Рис. 2 Составление фигур из треугольников
2. Из 9 палочек составить 4 равных треугольника. Подумать, как это можно сделать, рассказать, затем выполнять задание.
После этого воспитатель предлагает детям нарисовать мелом на доске составленные фигуры и рассказать о последовательности выполнения задания.
Вопросы для анализа: "Как составил 4 равных треугольника из 9 палочек? Какой из треугольников составил первым? Какие фигуры получились в результате и сколько?"
Воспитатель, уточняя ответы детей, говорит: "Начинать составлять фигуру можно с любого треугольника, а потом к нему пристраивать другие справа или слева, сверху или снизу".
3. Пример
Цель. Упражнять детей в самостоятельных поисках путей составления фигур на основе предварительного обдумывания хода решения.
Ход работы. Воспитатель задает детям вопросы: "Из скольких палочек можно составить квадрат, каждая из сторон которого равна одной палочке? 2 квадрата? (из 8 и 7). Как будете составлять 2 квадрата из 7 палочек?"
1. Отсчитать 10 палочек и составить из них 3 равных квадрата. Подумать, как надо составлять, и рассказать.
По мере выполнения воспитатель вызывает нескольких детей зарисовать составленные ими фигуры на доске и рассказать последовательность составления. Предлагает всем детям составить фигуру из 3 равных квадратов, расположенных в ряд, по горизонтали. На доске рисует такую же и говорит: "Посмотрите на доску. Здесь нарисовано, как можно по-разному решать эту задачу. Можно пристраивать к одному квадрату другой, а затем и третий. (Показывает.) А можно составить прямоугольник из 8 палочек, затем разделить его на 3 равных квадрата 2 палочками". (Показывает.) Затем задает вопросы: "Какие фигуры получились и сколько? Сколько прямоугольников получилось? Найдите и покажите их".
|
|
|
2. Из 5 палочек составить квадрат и 2 равных треугольника. Сначала рассказать, а затем составлять.
При выполнении этого задания дети, как правило, допускают ошибку: составляют 2 треугольника усвоенным способом - пристроением, в результате чего получается четырехугольник. Поэтому воспитатель обращает внимание ребят на условие задачи, необходимость составления квадрата, предлагает наводящие вопросы: "Сколько палочек нужно для составления квадрата? Поскольку у вас палочек? Можно ли составить, пристраивая 1 треугольник к другому? Как составить? С какой фигуры надо начинать составлять?" После выполнения задания дети объясняют, как они делали: надо составить квадрат и разделить его 1 палочкой на 2 равных треугольника.
4. Пример
Цель. Упражнять детей в умении высказывать предположительное решение, догадываться.
Ход работы. 1. Из 9 палочек составить квадрат и 4 треугольника. Подумать и сказать, как надо составлять. (Несколько детей высказывают предположения.)
Если дети затрудняются, воспитатель советует: "Вспомните, как составляли из 5 палочек квадрат и 2 треугольника. Подумайте и догадайтесь, как можно выполнить задание. Тот, кто первым решит задачу, зарисует полученную фигуру на доске".
После выполнения и зарисовки ответа воспитатель предлагает всем детям составить у себя одинаковые фигуры (рис. 3).

Рис. 3 Составление фигур из треугольников
Вопросы для анализа: "Какие геометрические фигуры получились? Сколько треугольников, квадратов, четырехугольников? Как составляли? Как удобнее, быстрее составлять?"
2. Из 10 палочек составить 2 квадрата - маленький и большой.
3. Из 9 палочек составить 5 треугольников.
При необходимости в ходе выполнения второго и третьего заданий воспитатель дает наводящие вопросы, советы: "Сначала подумайте, затем составьте. Не повторяйте ошибок, ищите новый ход решения. Говорится ли в задаче о размере треугольников? Это задачи на смекалку, надо сообразить, догадаться, как решить задачу".
Итак, в начальный период обучения детей 5 лет решению простых задач на смекалку они самостоятельно, в основном практически действуя с палочками, ищут путь решения. С целью развития у них умения планировать ход мысли следует предлагать детям высказывать предварительные рассуждения или сочетать их с практическими пробами, объяснять способ и путь решения.
Возможно несколько видов решения задач первой группы. Усвоив способ пристроения фигур при условии общности сторон, дети очень легко и быстро дают 2-3 варианта решения. Каждая фигура при этом отличается от прежней пространственным положением. Одновременно дети осваивают способ построения заданных фигур путем деления полученной геометрической фигуры на несколько (четырехугольник или квадрат на 2 треугольника, прямоугольник - на 3 квадрата).
Решение с детьми 5-6 лет более сложных задач на перестроение фигур следует начинать с тех, в которых с целью изменения фигуры надо убрать определенное количество палочек и наиболее простых - на перекладывание палочек.
Процесс поисков детьми решения задач второй и третьей групп гораздо сложнее, нежели первой группы. Для этого нужно запомнить и осмыслить характер преобразования и результат (какие фигуры должны получиться и сколько) и постоянно в ходе поисков решения соотносить его с предполагаемыми или уже осуществленными изменениями. В процессе решения необходим зрительный и мыслительный анализ задачи, умение представить возможные изменения в фигуре.
Таким образом, в процессе решения задач дети должны овладеть такими мыслительными операциями анализа задачи, в результате которых можно представить мысленно различные преобразования, проверить их, затем, отбросив неверные, искать и пробовать новые ходы решения. Обучение должно быть направлено на формирование у детей умения обдумывать ходы мысленно, полностью или частично решать задачу в уме, ограничивать практические пробы.
В какой последовательности надо предлагать детям 5-6 лет задачи на смекалку второй и третьей групп?
В фигуре, состоящей из 5 квадратов, убрать 4 палочки, оставив один прямоугольник (рис. 4).
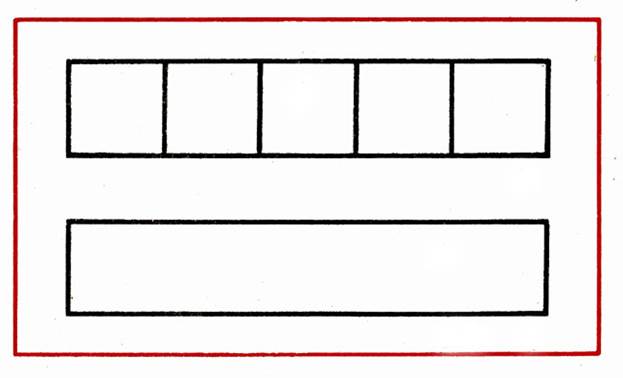
Рис. 4
В фигуре, состоящей из 6 квадратов, убрать 2 палочки, чтобы осталось 4 равных квадрата (рис. 5).
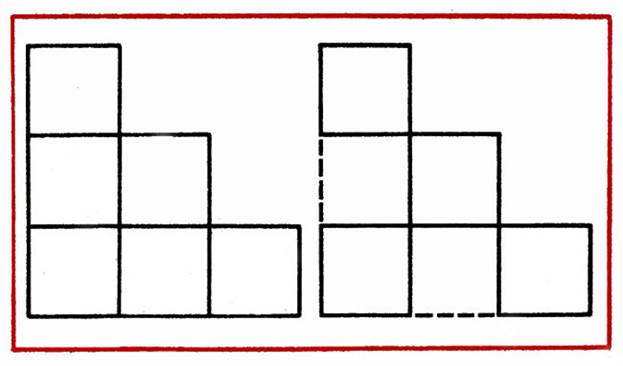
Рис. 5
Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы получился флажок (рис. 6).
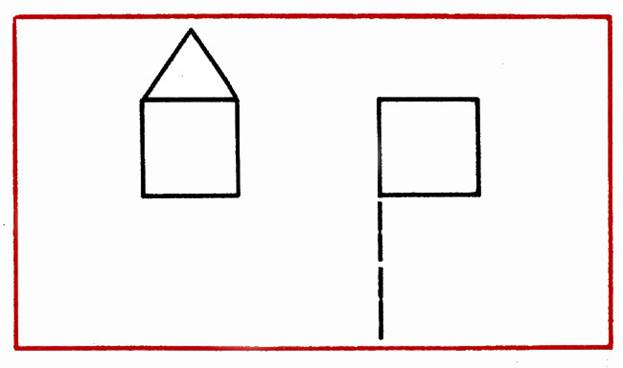
Рис. 6
В данной фигуре переложить 2 палочки, чтобы получилось 3, равных треугольника (рис. 7)
 .
.
Рис. 7
В фигуре, состоящей из 5 квадратов, убрать 3 палочки, чтобы осталось 3 таких же квадрата (рис. 8).

Рис. 8
В фигуре, состоящей из 4 квадратов, убрать 2 палочки, чтобы осталось 2 неравных квадрата (рис. 9).

Рис. 9
В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 2 неравных квадрата (рис. 10).

Рис. 10
В фигуре из 5 квадратов убрать 4 палочки, чтобы остались 3 квадрата (рис. 11).

Рис. 11
В фигуре из 4 квадратов переложить 2 палочки так, чтобы получилось 5 квадратов (рис. 12).

Рис. 12
В фигуре из 5 квадратов убрать 4 палочки, чтобы осталось 3 квадрата (рис. 13).

Рис. 13
Для этих и других аналогичных задач на смекалку характерно то, что преобразование, необходимое для решения, ведет к изменению количества квадратов, из которых составлена заданная фигура (задачи 2, 5 и др.), изменению их размера (задачи 6, 7), видоизменению фигур, например преобразование квадратов в прямоугольник в задаче 1.
В ходе занятий с целью руководства поисковой деятельностью детей воспитатель пользуется различными приемами, способствующими воспитанию у них положительного отношения к длительному настойчивому поиску, но в то же время быстроты реакции, отказа от выработанного пути поисков. Интерес детей поддерживается желанием достичь успеха, для чего нужна актив-, ная работа мысли.
Преобразование одной фигуры в другую. Изменение количества квадратов в фигуре.
1. Пример
Цель. Упражнять детей в умении решать задачи путем целенаправленных практических проб и обдумывания хода решения.
Материал: счетные палочки у детей, у воспитателя - изображенные графически задачи (на этом и следующих занятиях).
Ход работы. 1. Воспитатель показывает детям таблицу с изображенной на ней фигурой, предлагает составить из палочек такую же (рис. 4). Рассматривает ее вместе с детьми, определяет количество квадратов. Затем говорит: "Это задача. Послушайте, что нужно сделать, чтобы решить ее. Надо догадаться, какие 4 палочки убрать, чтобы получился 1 прямоугольник. Сначала подумайте, как это можно сделать, а затем убирайте палочки".
После того как будет решена задача, воспитатель вызывает одного ребенка к доске, тот показывает и рассказывает, как нужно ее решить. Педагог одобряет попытки детей действовать самостоятельно.
2. Дана фигура из 6 квадратов. Надо убрать 2 палочки, чтобы осталось 4 таких же квадрата (рис. 5).
После составления детьми по образцу такой фигуры идет анализ по вопросам: "Сколько квадратов в фигуре? Как расположены? Как считаете, какие из палочек, образующих квадраты, надо убрать, чтобы сразу уменьшилось их количество?"
Дети самостоятельно решают задачу. Воспитатель в случае затруднения помогает им, ориентируя на поиск правильных способов.
2. Пример
Цель. Упражнять детей в умении осуществлять целенаправленные пробы, ограничивать количество практических проб за счет обдумывания хода поисков, догадки.
Ход работы. 1. Дана фигура из 5 квадратов. Надо убрать 3 палочки, оставив 3 квадрата (рис. 8). Воспитатель задает вопросы, побуждает детей к решению задачи: "Сколько квадратов в фигуре? Сколько должно остаться? Сколько палочек нужно убрать? Эта задача на смекалку, надо догадаться, какие 3 палочки нужно убрать, чтобы квадратов стало меньше - 3?"
Дети приступают к решению. Воспитатель напоминает о необходимости предварительного обдумывания хода поисков решения. В случае затруднения он напоминает условие задачи, предлагает не повторять пробных действий, которые не приводят к правильному решению.
Один из детей, решивших задачу в числе первых, зарисовывает и объясняет решение у доски.
2. Дана фигура из 4 равных квадратов. Надо убрать 2 палочки, чтобы получилось 2 неравных квадрата (рис. 9).
Вопросы для анализа составленной по образцу фигуры: "Сколько квадратов? Можете ли доказать, что они равны? Подумайте, как решить задачу".
По предложению воспитателя один ребенок объясняет у доски решение задачи.
3. Пример
Цель. Высказывать предположительный ход поиска решения, проверять его путем целенаправленных поисковых действий.
Ход занятия. 1. Дана фигура из 5 равных квадратов; надо убрать 4 палочки, чтобы стало 3 равных квадрата (рис. 13).
Воспитатель, обращаясь к детям, говорит: "Рассмотрите фигуру, подумайте, как можно решить задачу, какие из палочек убрать, чтобы изменилась эта фигура. Сначала расскажите, а потом убирайте палочки".
Воспитатель спрашивает некоторых детей (но так, чтобы их рассказы не слышали другие ребята), предлагает всем решить задачу самостоятельно. Дети объясняют решение задачи у доски, с тем, чтобы по ходу рассказа можно было сделать зарисовку фигур.
2. Дана фигура из 4 квадратов: надо переложить 2 палочки, чтобы получилось 5 равных квадратов (рис. 12).
Воспитатель после составления детьми фигуры и анализа задачи говорит детям, чтобы они, прежде чем переложить палочки, подумали, ведет ли это действие к увеличению количества квадратов, рассказали о том, как они думают решать задачу. В ходе проверки решения воспитатель подчеркивает, что решить задачу можно по-разному.
В процессе обучения на занятиях, дети 5-6 лет активно включаются не только в практический поиск решения, но и в умственный. Об этом свидетельствуют их высказывания, рассуждения о путях решения. Так, детям была дана фигура из 5 квадратов; надо убрать 4 палочки, чтобы осталось 3 таких же квадрата (рис. 14). Отвечая на вопрос воспитателя о том, как будут решать задачу, одни отвечают: "Я беру вот эти палочки (а, б и к) и эту (в). Что же тогда получится? (Задумывается.) Нет, не знаю как". Другие рассуждают: "Я думаю, что убрать надо 2 угловые палочки (е, ж) и еще где-то посмотреть надо". "Я догадалась. Посмотрела и догадалась: если эти убрать (показывает на г, д, и, з), то будет 3 квадрата: один, два, три".

Рис. 14
В ходе выполнения заданий дети овладевают умением на основе обдумывания процесса поиска (анализа задачи) предполагать решение, проверять его практически, искать новые пути, обосновывать их.
Для обучения детей самостоятельному анализу задачи, поиску решения, умению догадываться целесообразно использование различных методических приемов, указаний о необходимости поискового подхода к решению задачи: "Сначала подумайте, как бы вы решили задачу, и расскажите об этом. Проверьте свое предположение, переложив палочки или даже не трогая их. Если считаете, что ошиблись, надо придумать, как решить задачу по-другому, а не повторять своих ошибок. Надо внимательно рассмотреть фигуру и догадаться, как решить задачу". Оценка, подтверждение правильности или ошибочности хода: "Эту палочку ты убрал правильно, подумай, как дальше решать задачу" - и другое стимулируют активность ребят, помогают им находить правильное решение.
В работе с детьми 7-го года жизни усложняется характер задач на преобразование фигур. Решаются они путем сочетания практических и мысленных проб или только в плане умственного действия - в уме, с обоснованием, выражением в речи хода решения.
Последовательность выполнения детьми 6-7 лет задач на преобразование фигур.
Переложить 1 палочку чтобы домик был перевернут в другую сторону (рис. 15).

Рис. 15
В фигуре, состоящей из 9 квадратов, убрать 4 палочки, чтобы осталось 5 квадратов (рис. 16).

Рис. 16
В фигуре из 6 квадратов убрать 3 палочки, чтобы осталось 4 квадрата (рис. 17).

Рис. 17
В фигуре, похожей на ключ, переложить 4 палочки, чтобы получилось 3 квадрата (рис. 18).

Рис. 18
В фигуре из 6 квадратов убрать 2 палочки так, чтобы осталось 4 равных квадрата (рис. 19).
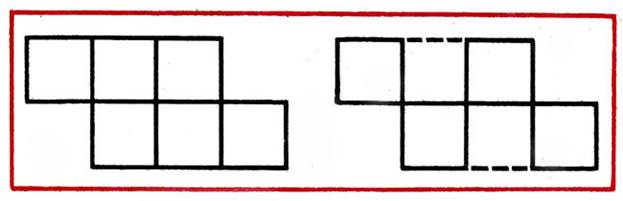
Рис. 19
В фигуре, изображающей стрелу, переложить 4 палочки так, чтобы получилось 4 треугольника (рис. 20).

Рис. 20
В фигуре из 5 квадратов переложить 3 палочки, чтобы стало 4 квадрата (рис. 21).

Рис. 21 В фигуре переложить 3 палочки так, чтобы получилось 4 равных треугольника 
Рис. 22
В фигуре, состоящей из 4 квадратов, переложить 3 палочки так, чтобы получилось 3 таких же квадрата (рис.23).
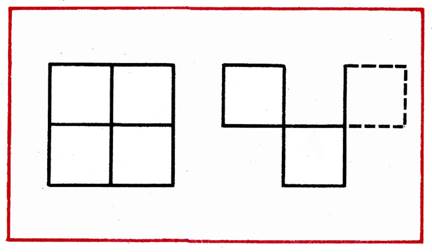
Рис. 23
Переложить 4 палочки так, чтобы из топора получилось 4 равных треугольника (рис. 24).
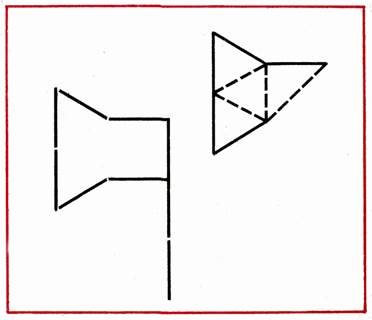
Рис.24
В фигуре, напоминающей фонарь, переложить 4 палочки, чтобы получился четырехугольник, состоящий из 4 равных треугольников (рис. 25).

Рис. 25
Переложить 2 палочки так, чтобы фигура; похожая на корову, смотрела в другую сторону (рис. 26).

Рис. 26
Какое наименьшее количество палочек нужно переложить, чтобы убрать мусор из совочка? (рис. 27.)

Рис. 27
В подготовительной к школе группе обучение детей решению задач на смекалку способствует дальнейшему развитию их умственной деятельности, способности планировать ход поисков.
Примеры (для детей 6-7 лет)
Преобразование фигур
1. Пример
Цель. Упражнять детей в умении осуществлять целенаправленные поисковые действия умственного и практического плана, частичном мысленном решении задачи.
Ход работы. Воспитатель сообщает детям: "Сегодня будем решать новые, более сложные задачи на смекалку. Составьте из палочек вот такую фигуру (показывает) и расскажите, из каких геометрических фигур она состоит".
1. Дана фигура из 6 квадратов. Надо убрать 2 палочки, чтобы осталось 4 квадрата (рис. 19).
Воспитатель помогает детям в нахождении способов решения: "Подумайте, какие палочки надо убрать, чтобы квадратов стало меньше. Не торопитесь перекладывать палочки, сначала подумайте, как надо решать задачу. Убирать палочки можно только в том случае, если уменьшается количество квадратов в фигуре".
Решение задачи проверяется у доски.
2. Дана фигура, похожая на стрелу. Надо переложить 4 палочки, чтобы получилось 4 треугольника (рис. 20).
После анализа и уточнения условия задачи воспитатель спрашивает, кто из детей уже догадался, как решить ее. По заданию воспитателя некоторые дети высказывают предположительное решение так, чтобы не слышали другие. Воспитатель предлагает им проверить догадки практически. Поощряет действия, направленные на мысленное решение задачи, рассуждения, подчеркивает, что эта задача имеет несколько решений, которые зарисовываются на доске.
2. Пример
Цель. Планировать в уме полный или частичный ход решения, представлять изменения, которые произойдут в фигуре в результате преобразования, высказывать предположения.
Ход работы. В фигуре, похожей на лампу, переложить 3 палочки так, чтобы стало 4 равных треугольника (рис. 22).
Вопросы для анализа: "Как вы считаете, какие палочки и куда надо переложить? Что изменится в результате этого?"
Воспитатель предлагает детям высказать свои предположения и решать задачу.

Рис. 28
В случае неправильного хода поисков (как показано на рис. 28) воспитатель поясняет, что при решении некоторых головоломок геометрические фигуры (треугольники, квадраты) могут находиться на расстоянии одна от другой.
3. Пример
Цель. Учить детей решать задачи на основе мысленного анализа путем выдвижения Гипотезы (предположения) и проверки ее.
Материал: магнитная доска с составленной на ней из палочек фигурой.
Ход работы. В фигуре фонаря переложить 4 палочки так, чтобы получился четырехугольник, состоящий из 4 равных треугольников (рис. 24).
Воспитатель говорит детям: "Вы решали много задач на составление фигуры из палочек. Эту задачу составлять из палочек не будете. Смотрите на доску, где зарисована эта задача, и попробуйте решить ее". Затем задает вопросы: "Из. скольких палочек составлена фигура фонаря? Сколько палочек нужно переложить, чтобы получилась другая фигура? Какая фигура должна получиться? Рассмотрите этот четырехугольник (показывает верхнюю часть фигуры). Какие здесь фигуры? Как можно составить такую фигуру?"
Далее детям предлагается проверить на магнитной доске ход решения, который они считают верным. Неверные пути дважды практическим способом не проверяются; в таких случаях воспитатель стимулирует поиск нового пути решения.

Рис. 29
В подготовительной к школе группе многие дети при условии систематического обучения целенаправленно анализируют задачи на смекалку и обнаруживают простые рациональные способы их решения. Так, в задаче по преобразованию стрелы в 4 равных треугольника (показана на рис. 29) дети осмысленно объясняют возможные преобразования. Например, рассуждают: "Я вот так переложу палочки: эту (а) сюда, эту и эту (б и в) тоже вниз, чтобы получились треугольники, а эту (ж)... сейчас подумаю, куда ее положить... Вниз можно или сюда, и должно получиться 4 треугольника (рис. 29, б)", "Я думаю так решить эту задачу: 3 палочки (з, и, к) положить вот так, сверху, получится 3 треугольника, а эту (ж) - она ведь здесь не нужна - я положу сверху, получатся 4 треугольника, мы так раньше составляли" (рис. 29, в).
В ходе обучения время поиска детьми решения задачи сокращается, меняется характер проб, обдумывание решения начинает занимать все большее место. Поэтому на определенном этапе предложенную задачу дети смогли решить, анализируя ее на основе только графического изображения. Практическое составление и видоизменение фигур служило здесь средством проверки.
В результате регулярно организуемых педагогом занятий, упражнений по решению задач-головоломок дети приобретают способность подходить к каждой нестандартной задаче творчески, с позиции поиска нового пути решения, а не использования уже известного им. Характер поисковых действий при этом постепенно меняется: от практических ("проб и ошибок") - к целенаправленным практическим действиям (с целью намеченного преобразования), и от них - к мысленным пробам через предугадывание пути решения.
От решения задач-головоломок с помощью воспитателя (на основе частичных подсказок, использования наводящих вопросов, подтверждения частичного решения) дети переходят к полностью самостоятельному быстрому решению задач.
Дети 6-7 лет могут сами придумывать элементарные задачи на смекалку (головоломки с палочками). Для этого педагогу необходимо провести с детьми беседу о том, как придумываются такие задачи, что в них задано (какая-либо фигура), какое преобразование требуется осуществить (видоизменить фигуру, уменьшить или увеличить количество квадратов, треугольников, прямоугольников).
Головоломки с палочками, придуманные детьми:
Переложить 6 палочек, чтобы из корабля получился танк (рис. 30, а). (Ренат М., 6 лет 10 мес.)
В фигуре переложить 3 палочки, чтобы получился воздушный змей (рис. 30, б). (Лена М., 7 лет.)
Переложить 5 палочек, чтобы из вазы получился телевизор (рис. 30, в).
Переложить 1 палочку так, чтобы получилось 5 равных квадратов (рис. 30, г).
Переложить 3 палочки так, чтобы получилось 4 равных треугольника (рис. 30, д). (Илья М., 4 года 7 мес.).

Головоломки с палочками
Эти задачи очень просты, в каждой из них требуется произвести преобразование фигур путем перекладывания палочек. Они придуманы детьми по аналогии с теми задачами, что решались ими ранее, но, безусловно, являются показателем более высокого уровня развития пространственного представления, мышления.
Дети способны представить возможные пространственные, качественные изменения не только в ходе решения предложенной им задачи, но и в составляемой ими самостоятельно. Все это свидетельствует о развитии у них смекалки и сообразительности. При этом смекалку следует понимать как способность быстро устанавливать связи между частями задачи, направлять решение на правильный поиск его, исключая при этом ошибочный путь, отбрасывать несущественные элементы задачи.
Только на основе анализа условий задачи, самостоятельных поисков в результате овладения умственными операциями (обобщение, сравнение, анализ и др.) становится возможным проявление смекалки и самостоятельное умозаключение.
По мере овладения детьми приемами решения задач изменяется соотношение действий и рассуждений в ходе их решения. В начале обучения дети с трудом обосновывают свои до конца неосознанные практические действия, поэтому и процесс поиска складывается в основном из одних практических проб. Словесное выражение хода решения отражено в замечаниях: "Эти возьму", "Сюда положу", "Так нужно" и др. Под влиянием упражнений у детей начинают преобладать рассуждения, действия же становятся более целесообразными, сокращается их количество, назначение. Меняется характер и роль рассуждений: от рассуждений в процессе практических действий - к рассуждениям, предваряющим эти действия (выдвижение предположения, гипотезы решения). Кроме того, меняется качество рассуждений, которые сопровождают практические действия. Дети 6-7 лет аргументируют решение, доказывают правильность или ошибочность хода, исходя из данных задачи и цели трансфигурации. Они овладевают умением предполагать решение и проверять его без практических действий, т. е. в процессе умственного действия находить правильное решение задачи.
Задачи-смекалки геометрического характера частично включаются непосредственно в содержание занятий по формированию элементарных математических представлений в старшей и подготовительной к школе группах с целью активизации детской мысли, развития логического мышления, выработки умения догадываться, смекалки и сообразительности, что важно человеку для жизни, трудовой деятельности. При этом следует соблюдать строгую последовательность в усложнении самих задач, требований к организации поиска решения их детьми. - От занятия к занятию уточняется и усложняется анализ задач, характер поисковых действий, уровень проявления самостоятельности мышления и решения, сочетание действий и рассуждений.
|
|
|


