для комплексной контрольной работы

Вопросы по дисциплине «Математика»

№1. 1. Сформулировать понятие множества. Изложить действия над множествами, разъяснить их суть и перечислить их свойства.

2. Запишите множество А, элементы которого - натуральные числа от 1 до 10 и множество В, элементами которого являются делители числа 24.

3. Найдите:

1) объединение А и В; 2) пересечение А и В; 3) разность А и В.

 

№2. 1. Опишите основные элементы математической логики. сформулируйте законы алгебраической логики, определите простейшие операции над высказываниями.

2. Сформулируйте отрицания следующих высказываний:

1)Число 4 удовлетворяет неравенству х<8 и неравенству x>2,5.

2) Не все простые числа нечётные.

Для каждого из высказываний укажите, что является истинным: само высказывание или его отрицание.

3. Приведите примеры дизъюнкции, конъюнкции, импликации и эквиваленции высказываний из элементарной математики.

 

№3. 1. Изложить принцип математической индукции. Определить шаги индукции. Раскрыть сущность метода математической индукции.

2. Запишите шаги индукции для доказательства равенства .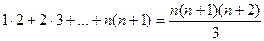

3. Докажите данное равенство, пользуясь методом математической индукции (выполните третий шаг индукции).

№4.. 1. Сформулировать теорему и записать формулу бинома Ньютона. Перечислить свойства бинома. Записать формулу для вычисления биномиальных коэффициентов.

2. Вычислите .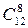

3. Найдите 9-й член в разложении бинома Ньютона

 

№5. 1. Дать определение целой рациональной и дробно-рациональной функции, правильной и неправильной рациональной дроби.

2. Из заданных дробей выбрать правильные дроби

; ; ; ; ; ..

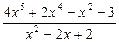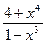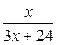3. Из неправильной дроби 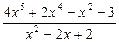выделите целую часть и запишите указанную дробь в виде суммы целой части и правильной дроби.

 

№6. 1. Назвать виды простейших дробей и записать их формулы. Изложить суть разложения рациональной дроби на сумму простейших дробей.

2. Из заданных дробей выбрать простейшие дроби и указать их тип:

; ; ; ; ; ; ; ; ; .

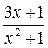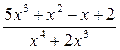3.. Представьте данную правильную дробь в виде суммы простейших дробей с неопределенными коэффициентами в числителях дробей (без вычисления коэффициентов):

; 3) 4)

 

№7. 1. Записать формулы представления рациональной дроби в виде суммы простейших дробей с неопределенными коэффициентами. Изложить метод неопределенных коэффициентов.

2. Проверьте правильность найденных коэффициентов разложения .

3. Представьте данную правильную дробь в виде суммы простейших дробей с неопределенными коэффициентами в числителях дробей и вычислите коэффициенты разложения:

 

№8. 1..Дать понятие комплексного числа. Записать три формы представления комплексных чисел. Дать геометрическую интерпретацию комплексного числа и его изображения на комплексной плоскости, действительной и мнимой части комплексного числа, его модуля и аргумента.

2. Даны комплексные числа: z₁=-4 и z₂=4+4i.

Найдите: а) действительную и мнимую части указанных чисел;

б) числа, комплексно-сопряженные данным

3. Найдите: а) модули и аргументы указанных чисел; б) запишите указанные числа в тригонометрическом и показательном виде.

 

№9. 1. Записать формулу тригонометрического представления комплексного числа, определить действия над числами в тригонометрической форме, записать соответствующие формулы.

2. Даны комплексные числа и . Укажите модуль и аргумент каждого числа, найдите их произведение и частное.

3. Вычислите а) 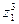; б) .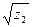

№10. 1. Дать определение матрицы, определить виды матриц. Изложить линейные операции над матрицами и их свойства, записать соответствующие формулы.

2. Найдите линейную комбинацию двух матриц , если , , , .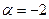

3. Проверить, коммутируют ли матрицы и .

 

№11. 1. Дать определение определителя квадратной матрицы. Записать формулы для вычисления определителей 2-го порядка. Сформулировать правило Саррюса и теорему Лапласа и записать соответствующие формулы для вычисления определителя 3-го порядка.

2.1)Вычислите определитель второго порядка: ;

2) Вычислите определитель 3-го порядка (любым из способов).

№12.. 1.. Дать определение определителя квадратной матрицы. Изложить свойства определителя, способы вычисления определителей

2. В ычислите определитель 2-го порядка 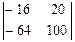, используя его свойства

3. Вычислите определитель методом понижения его порядка .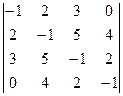

 

№13. 1. Определить понятие обратной матрицы. Изложить ее свойства. Изложить алгоритм вычисления обратной матрицы.

2. Определите, существует ли матрица, обратная для заданной матрицы . Ответ поясните.

3. Найти матрицу, обратную для А. и выполнить проверку.

 

№14.. 1. Дайте определение минора порядка k для произвольной матрицы, ранга и базисного минора матрицы. Приведите примеры. Назовите способы нахождения ранга матрицы

2. Определите, между какими значениями заключается ранг матрицы А= .

3. Определите ранг матрицы А любым способом и укажите какой-нибудь базисный минор.

№15. 1.Определить понятия системы линейных алгебраических уравнений с n неизвестными, ее решения, совместности, определенности, несовместности, неопределенности, эквивалентности, эквивалентных преобразований. Сформулировать критерий совместности системы.

2. Дана расширенная матрица системы . Запишите систему, соответствующую данной матрице. Пользуясь критерием Кронекера-Капелли, сделайте вывод о совместности либо несовместности данной системы.

3. Дана расширенная матрица системы .. Запишите систему, соответствующую данной матрице. Найдите все базисные решения данной системы.

 

№16. 1. Записать систему линейных алгебраических уравнений в матричном виде. Изложить сущность решения систем линейных алгебраических уравнений методом обратной матрицы.

2. Запишите систему в матричном виде и найдите неизвестные с помощью обратной матрицы.

3. Решите матричное уравнение .

 

№17. 1.. Сформулировать теорему Крамера. Записать формулы Крамера. Раскрыть сущность решения систем линейных алгебраических уравнений методом Крамера.

2. Пользуясь формулами Крамера, решите систему .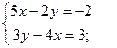

3. При каком значении параметра a система имеет единственное решение? Найдите это решение.

№18. 1. Изложить алгоритм метода Гаусса, раскрыть его сущность и виды решений в зависимости от полученной ступенчатой матрицы. Определить понятие базисных и свободных неизвестных, общего и частного решения для систем с бесконечным множеством решений.

2. Составьте расширенную матрицу системы .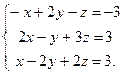

3. С помощью метода Гаусса найти неизвестные в системе.

 

№19. 1. Дать понятие вектора на плоскости и в пространстве, определить линейные операции над векторами в геометрической форме, изложить их свойства.

2. Вектор 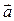задан координатами точки начала и конца , вектор задан координатами точек начала и конца и . Изобразите данные векторы в прямоугольной декартовой системе координат на плоскости.

3. Постройте векторы и на той же плоскости.

 

№20. 1. Дать понятие базиса на плоскости и в пространстве, сформулировать теоремы о разложении произвольного вектора по базису на плоскости и в пространстве. Определить понятия проекции точки и вектора, координат вектора в данном базисе. Записать формулу для вычисления длины вектора

2. Дан вектор . Написать разложение данного вектора по векторам прямоугольного декартова базиса.

3. Найти координаты и составляющие вектора ., вычислить его длину.

 

№23. 1. Изложить понятие прямоугольной декартовой системы координат. Определить линейные операции над векторами в прямоугольных декартовых координатах и записать соответствующие формулы.

2. Даны векторы и . Найти векторы и .

3. Являются ли данные векторы коллинеарными?

.

№21. 1. Дать определение скалярного произведения векторов, изложить его свойства, записать формулу для вычисления в координатной форме. Изложить механический смысл скалярного произведения.

2. При каком значении λ векторы и взаимно перпендикулярны?

3. В треугольнике с вершинами А(2; -1; 3), В(1; 1; 1) и С(0;0;5) определите угол при вершине А.

 

№22. 1. Дать определение векторного произведения векторов: изложить его свойства, геометрический смысл, вычисление в координатной форме.

2. Даны векторы 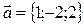и 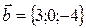.. Найти их векторное произведение

3. Вычислить площадь параллелограмма, построенного на данных векторах.

 

№24. 1. Дать определение смешанного произведения векторов, изложить его свойства, геометрический смысл, вычисление в координатной форме.

2. Проверьте компланарность векторов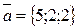

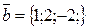
3. Вычислите высоту наклонного параллелепипеда, построенного на данных векторах.

 

№25. 1. Дать понятие числовой функции, ее области определения и области значений. Определить способы задания функции. Сформулировать простейшие свойства. функций

2. Для функции 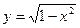найти ее область определения, область значений, нули функции, доказать ее четность.

3. Построить график заданной функции.

№26. 1. Дать понятие обратной и сложной функции, неявно заданной функции, параметрически заданной функции.

2. Найдите функцию, обратную для если она существует.

3. Постройте графики указанных функций в одной системе координат и найдите их точки пересечения.

 

№27 1. Определить способы задания прямой на плоскости и вывести различные виды уравнений прямой на плоскости в зависимости от способа задания..

2. Составить уравнение высоты ADтреугольника, заданного точками , , ..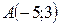

3. Записать различные виды уравнений полученной прямой, определить ее угловой коэффициент, построить на плоскости Оху.

 

№28. 1. Разъяснить критерии определения взаимного расположения прямых на плоскости в зависимости от видов уравнений прямых. Записать условия параллельности и перпендикулярности прямых. Дать определение угла между двумя прямыми и расстояния от точки до прямой. Записать формулы для определения угла между двумя прямыми и расстояния от точки до прямой.

2. Найти угол между прямыми х + 5у – 3 = 0 и 2х – 3у + 4 = 0.

3. Написать уравнение прямой, проходящей через точку , параллельной прямой 2х – 3у + 4 = 0, и найти расстояние между указанными прямыми.

№29. 1. Дать определение окружности, записать ее геометрическое, каноническое, нормальное, параметрические и алгебраическое уравнения., сформулировать геометрические свойства.

2. Написать уравнение окружности радиуса 2 с центром в точке (-1; 4).

3. Найти координаты центра и радиус окружности

 

№30. 1. Дать определение эллипса, записать его геометрическое, каноническое, нормальное, параметрические и алгебраическое уравнения, определить основные параметры., сформулировать геометрические свойства.

2. Написать каноническое уравнение эллипса с фокусами на оси Ох, если его большая ось равна 8, а малая – 6.

3. Доказать, что кривая, определяемая уравнением , является эллипсом, найти его центр симметрии, большую и малую оси.

 

 

Преподаватель О.В.Гальцова

 

 

РАССМОТРЕНО

на заседании цикловой комиссии

естественно-математических дисциплин,

протокол №__ от «___»__________2011

Председатель комиссии______________ И.В. Алексеенко

 

Поделиться:

Воспользуйтесь поиском по сайту: