 |
Определение параметров рабочего тела в точках цикла
|
|
|
|
Содержание
Задание
1. Расчет начальных параметров
1.1 Молярная масса газовой смеси
1.2 Газовая постоянная рабочего тела (смеси газов)
1.3 Массовые теплоемкости газовой смеси
1.4 Показатель адиабаты.
2. Определение параметров рабочего тела в точках цикла
3. Расчет процесса цикла
3.1 Процесс адиабатного состояния
3.2 Процесс подвода теплоты по изохоре
3.3 Процесс подвода теплоты по изобаре
3.4 Процесс адиабатного расширения
3.5 Процесс отвода теплоты по изохоре
4. Расчет характеристик цикла
5. Исследование цикла
5.1 Влияние степени сжатия на термический КПД цикла
5.2 Влияние степени повышения давления на термический КПД цикла
5.3 Влияние степени изобарного расширения на термический КПД цикла
5.4 Анализ
Список используемой литературы
Приложение 1
Приложение 2
Задание
1 - Рассчитать идеальный цикл ДВС со смешанным подводом теплоты, который в соответствии с рисунком 1 включает следующие термодинамические процессы изменения состояния рабочего тела:
а) 1-2 - адиабатное сжатие;
б) 2-3 - подвод теплоты по изохоре;
в) 3-4 - подвод теплоты по изобаре;
г) 4-5 - адиабатное расширение;
д) 5-1 - отвод теплоты по изохоре.
q”1








 Р 3 4
Р 3 4
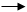 q’1
q’1

 2
2
5



 q2
q2
1

 V
V
Определить:
1.1 газовую постоянную рабочего тела;
1.2 значение давления, удельного объёма, температуры и энтропии во всех точках цикла;
1.3 для каждого из процессов, составляющих цикл, изменение внутренней энергии и энтальпии, значений теплоёмкости, теплоты и рабочего процесса;
1.4 характеристики цикла, в целом: количество подведенной и отведенной теплоты, среднее давление и термический КПД.
2 – Исследовать влияние степени сжатия, степени повышения давления и степени предварительного (изобарного) расширения на термодинамический КПД цикла.
|
|
|
Исследовать:
2.1 влияние степени повышения давления на термический КПД;
2.2 влияния степени сжатия на термический КПД;
2.3 влияние степени изобарного расширения на термический КПД.
Исходные данные для расчетов цикла ДВС.
| Состав компонентов рабочего тела,% | ε | λ | ρ | ||||
| СО2 | СО | Н2О | N2 | O2 | 18,5 | 1,5 | 2 |
| 8,5 | 6,5 | 10 | 75 | - | |||
Расчет начальных параметров
Молярная масса газовой смеси
μ=Σri*μi (1)
где n – число компонентов рабочего тела, n=4;
ri – объемная доля i-ого компонента в составе смеси;
μi – молярная масса i-ого компонента, кг/кмоль.
Рассчитываем молярную массу каждого компонента смеси:
μСО2=12+16*2=44 кг/кмоль
μСО=12+16=28 кг/кмоль
μN2=14*2=28 кг/кмоль
μН2О=1*2+16=18 кг/кмоль
Подставляя значения молярных масс каждого компонента в формулу (1), получаем общую молярную массу для газовой смеси:
μ=0,085*44+0,065*28+0,75*28+0,1*18
μ=28,36 кг/кмоль.
Газовая постоянная рабочего тела (смеси газов)
R=8314/μ (2)
где 8314 – постоянный коэффициент (константа);
μ – молекулярная масса газовой смеси, кг/кмоль
R=8314/28,36
R=293,1594 Дж/(кг*К)
R=0,293 кДж/(кг*К).
Массовые теплоемкости газовой смеси
-при постоянном объеме Сv вычисляют по формуле:
Сv=1/μ*Σri*μcvi (3)
где μcvi – молярная теплоемкость i-oro компонента смеси, при постоянном объеме, зависящая от атомности газа, кДж/(кг*К)
Определяем молярную теплоёмкость каждою из компонентов:
СО2 – трехатомный газ, μcv=29,3 кДж/(кмоль*К);
СО – двухатомный газ, μcv=20,8 кДж/(кмоль*К);
N2 – двухатомный газ, μcv=20,8 кДж/(кмоль*К);
Н2О – трехатомный газ, μcv=29,3 кДж/(кмоль*К);
Полученные значения подставляем в формулу (3)
Сv=1/28,36*(0,085*29,3+0,065*20,8+0,75*20,8+0,1*29,3);
Сv=0,7889 кДж/(кг*К).
-при постоянном давлении Ср вычисляют по формуле:
Ср=1/μ*Σri*μcpi (4)
|
|
|
где μcp – молярная теплоемкость i-ого компонента смеси, при постоянном давлении, зависящая от атомности газа, кДж/(кг*К)
Определяют молярную теплоемкость каждого из компонентов:
СО2 – трехатомный газ, μcр=37,6 кДж/(кмоль*К);
СО – двухатомный газ, μcр=29,12 кДж/(кмоль*К);
N2 – двухатомный газ, μcр=29,12 кДж/(кмоль*К);
Н2О – трехатомный газ, μcр=37,6 кДж/(кмоль*К);
Полученные значения подставляем в формулу (4):
Ср=1/28,36*(0,085*37,6+0,065*29,12+0,75*29,12+0,1*37,6);
Ср=1,0821 кДж/(кг*К).
Показатель адиабаты
k=Ср/Сv (5)
где Ср – массовая теплоемкость газовой смеси, при р=const, кДж/(кг*К);
С v – массовая теплоемкость газовой смеси, при v= const, кДж/(кг*К).
k=1,0821/0,7889
k=1,3717
Определение параметров рабочего тела в точках цикла
Для всех точек цикла определяют:
- давление Р, Па;
- температура Т, К;
- удельный объем V, м3/кг;
- энтропия S, кДж/(кг*К).
Точка 1.
Давление:
Р1=1 бар=105 Па.
Температура:
Т1=293 К.
Удельный объем:
V1=R*T1/P1 (6)
V1=293*293/105=0,859 м3/кг.
Энтропия:
S1= Сv*ln(T1/273)+R*ln((V1*μ)/22,4) (7)
S1=0,7889*ln(293/273)+0,293*ln((0,859*28,36)/22,4)
S1=0,0804 кДж/(кг*К).
где 273 – абсолютная термодинамическая температура, приблизительно соответствующая температуре тройной точки воды, т.е. нулю градусов Цельсия, К;
22,4 – объем, занимаемый 1 кмолем газа при нормальных физических условиях, м3.
Точка 2.
Давление.
Р2=Р1*εk (8)
Р2=105*18,51,3717
Р2=5,47 МПа.
где ε – степень сжатия рабочего тела.
Удельный объем:
V2=V1/ε (9)
V2=0,859/18,5
V2=0,0464 м3/кг.
Температура:
Т2=Т1*εk-1 (10)
Т2=293*18,50,3682
Т2=866,763 К.
Энтропия:
S2=S1 (11)
S2=0,0804 кДж/(кг*К).
Точка 3.
Удельный объем:
V3=V2; (12)
V3=0,0464 м3/кг.
Давление (степень повышения давления λ при изохорном подводе теплоты):
λ=Р3/Р2→Р3=λ*Р2 (13)
Р3=1,5*5,47
Р3=8,2 МПа.
где Р2 – давление в точки 2 цикла;
Р3 – в давление в точки 3 цикла.
Температура (изохора):
Р3/Р2=Т3/Т2→Т3=Р3*Т2/Р2 (14)
Т3=8,2*866/5,47
Т3=1300,1445 К.
где Т2 – температура в точке 2 цикла, К;
Т3 – температура в точке 3 цикла.
Энтропия S3:
S3=S2+Сv*ln(Т3/Т2) (15)
S3=0,0804+0,7889*ln(1300/866)
S3=0,4002 кДж/(кг*К).
где С v – массовая теплоемкость газовой смеси при постоянном объеме, Дж/кг*К;
S2 – энтропия в точке 2 цикла, кДж/(кг*К);
|
|
|
S3 – энтропия в точке 3 цикла, кДж/(кг*К).
Точка 4.
Так как в процессе 3-4 подвод теплоты осуществляется по изобаре, то есть Р=const, то давление Р4 в точке 4 цикла равно давлению Р3 в точке Р3 цикла:
Р4=Р3 (16)
Р4=8,2 МПа.
Удельный объем:
ρ=V4/V3→V4=ρ*V3 (17)
V4=2*0,0464
V4=0,0929 м3/кг.
где ρ – степень изобарного расширения.
Температура:
V3/V4=T3/T4→T4=V4*T3/V3 (18)
Т4=0,929*1300,1445/0,0464
Т4=2600,289 К.
где V3 – удельный объем в точке 3 цикла, м3/кг;
V4 – удельный объем в точке 4 цикла, м3/кг;
Т4 – температура в точке 4 цикла, К.
Энтропия:
S4=S3+Cp*ln(T4/T3) (19)
S4=0,4002+1,0821*ln(2600,289/1300,1445)
S4=1,1503 кДж/(кг*К).
Точка 5.
Удельный объем:
Так как в процессе 5-1 осуществляется отвод теплоты по изохоре, то есть V=const, то удельный объем V5 в точке 5 цикла равен удельному объему V1 в точке 1 цикла:
V5=V1 (20)
V5=0,859 м3/кг.
Давление:
Р5/Р4=(V4/V5)k→P5=P4*(V4/V5)k (21)
P5=8,2*(0,0929/0,859)1,3717
P5=0,388 МПа.
где Р5 – давление в точке 5 цикла, Па;
V5 – удельный объем в точке 5 цикла, м3/кг;
k – показатель адиабаты.
Температура:
Т5/Т4=(V4/V5)k-1→T5=T4*(V4/V5)k-1 (22)
Т5=2600,289*(0,0929/0,859)0,3717
Т5=1137,3331 К.
где Т5 – температура в точке 5 цикла, К;
V5 – удельный объем в точке 5 цикла, м3/кг.
Энтропия: Так как при адиабатном процессе изменения состояния рабочего тела происходит без теплообмена с внешней средой, то энтропия рабочего тела в точке 5 цикла не изменяется (S5=S4), поэтому энтропию рабочего тела в точке 5 цикла определяют из равенства:
S5=S4 (23)
S5=1,1503 кДж/(кг*К).
Результат расчетов представим в виде таблицы.
Параметры рабочего тела.
| Параметры рабочего тела. | Точки цикла | ||||
| 1 | 2 | 3 | 4 | 5 | |
| Р, Па | 100000 | 5472736 | 8209104 | 8209104 | 388168 |
| V,м3/кг | 0,8590 | 0,0464 | 0,0464 | 0,0929 | 0,8590 |
| Т, К | 293 | 866,7630 | 1300,1445 | 2600,2890 | 1137,3331 |
| S, кДж/(кг*К) | 0,0804 | 0,0804 | 0,4002 | 1,1503 | 1,1503 |
Расчет процессов цикла
Для каждого процесса цикла ДВС определяют следующие параметры:
- теплоемкость С, кДж/(кг*К);
- изменение внутренней энергии ΔU, кДж/кг;
- изменение энтальпии Δi, кДж/кг;
- количество подведенной или отведенной теплоты q, кДж/кг;
|
|
|
- работу расширения или сжатия l, кДж/кг.
|
|
|
12 |


