Теорема о существовании конечного предела интегральных сумм для непрерывных ф-ий

Вычисление интегралов от тригонометрических ф-ий.

1) ∫R(sinx, cosx)dx Замена перем-ных tg(x/2)=t (универ. тригонометр замена) sinx=2t/(1+t²) cosx=(1-t²)/ /(1+t²) dx=2/(1+t²)dt;∫R(2t/(1+t²), (1-t²)/ /(1+t²)) 2/(1+t²)dt=∫Ř(t)dt

2) ∫R(sinx) cosxdx=|sinx=t, cosxdx=dt|=∫R(t)dt

3) ∫R sinx(cosx)dx=|cosx=t, -sinxdx=dt|=-∫R(t)dt

4) ∫R(tgx)dx=|t=tgx, x=arctgt, dx=dt/(1+t²)|= ∫R(t)dt/(1+t²) 5) R(sinx, cosx)= R(-sinx, -cosx)

∫R(sinx, cosx)dx=|t=tgx, dx = dt/(1+ t²)| =∫Ř(t)dt

6) ∫sin ^m x cos ⁿ xdx

a)m=2k+1 ∫sin ^2k x cos ⁿ x sinxdx=∫(1-cos ² x)^k cos ⁿ x sinxdx=|t=cosx, dt=-sinxdx|=-∫(1-t ²)^k t ⁿ dt

b)n=2k+1 ∫sin ^m x cos ^2k x cosxdx= ∫sin ^m x (1-sin ² x)^k dsinx

7) ∫sin ^2p x cos ^2a xdx sin²x=(1-cos2x)/2

cos²x=(1+cos2x)/2 sinxcosx=(1/2)sin2x

8) m=-µ n=-ν замена t=tgx

1/ sin²x=1+ ctg²x 1/ cos²x=1+tg²x

9) ∫tg ^m x dx; ∫ctg ^m x dx, m-целое >0ое tg²x=1/ cos²x-1

сtg²x=1/ sin²x-1

10) ∫sinmxcosnxdx ∫sinmxsinnxdx

∫cosmxcosnxdx sinmxcosnx=(1/2)(sin(m+n)x+sin(m-n)x)

sinmxsinnx=(1/2)(cos(m-n)x-cos(m+n)x)

Теорема о существовании конечного предела интегральных сумм для непрерывных ф-ий

Пусть существует f определенная на замкнутом интервале [a,b] => ее интегр суммы стремяться к конечному пределу при ранге разбиения à 0.

ax²+bx+c=a(x+b/2a)+(4ac-b²)/(4a²) x+b/2a=t; (ax+b)/(cx+d)=t^k=>

ax+b= cx t^k+ dt^k=>x=…; dx=(…)dt

Замена переменной: ∫f(x)dx=|x= φ(t); t=g(x); dx= φ’(t)dt |=∫f(φ(t)) φ’(t)dt

Поднесение по знак дифф-ла: Если ∫f(x)dx=F(x)+C, то ∫f(n)dx=F(n)+C

интегрир по частям: ∫udv=uv-∫vdu

∫x sin x dx=|u=x; du=dx; dv=sin x dx; v= -cos x|=-xcos x-∫-cos xdx= -xcos x+sin x.

Ф-цию вида R(x,^mÖ(ax+b)/(cx+d) –называют дробно линейной ирр-тью. С помощью замены t=^mÖ(ax+b)/(cx+d) рационализируем интеграл. t^m= (ax+b)/(cx+d); x=(b-dt^m)/(ct^m-a) –рацион ф-ция от t; dx=(mt^m-1(ad-bc)dt)/(ct^m-a)² Þ òR(x,^mÖ(ax+b)/ (cx+d))dx=òR((b-dt^m)/ (ct^m-a),t) (mt^m-1(ad-bc)dt)/(ct^m-a)²= òR1(t)dt. R1(t)-рацион-ая. Вида òR(x,Öax²+bx+c)dx, -квадр-ая ирр-ть где а, b, c=const. Если трёхчлен ax²+bx+c имеет действит корни х1 х2 то ax²+bx+c=a(x-x1)(x-x2) и R(x,Öax²+bx+c)=R(x,(x-x1)Ö(x-x2)a/(x-x1)=R1(x,Ö(x-x2)/(x-x1); пусть ax²+bx+c не имеет действит корней и а>0. Тогда подстановка (Эйлера) t=Ö(ax²+bx+c) +xÖa Þax²+bx+c=t²-2xtÖa+ax²; x=(t²-c)/2t(Öa)+b –рацион функ-ция от t Ч.Т.Д; Если а<0 с>0 (ax²+bx+c)>=0) то можно сделать замену Öax²+bx+c=xt+Öc {}{}Опред интеграл. Ограниченность интегрируемой ф-ии. {O}Разбиением t[a,b] называется произвольное мн-во точек xi, I=0,1,…,it удовлетворяющее условию x0=a<x1<x2<…<xit-1<xit{} Каждый из отрезков [xi-1,xi] назыв отрезком разбиения t{} Пусть ф-ция y=f(x) определена на [a,b] и t произвольное разбиение этого отрезка, в каждом отрезке разбиения в произвольном образе выберем (.) xiÎ[xi-1,xi] I=1,..,it и рассмотрим сумму s_t(f,x1,…,xit)= å_I=1^ixf(xI)Dx; -интегральная сумма {Определение} Число I –называется опред ò ф-ции y=f(x) на отр[a;b] и обозначается _aò^bf(x)dx Если " E >0 $d_E=d(E)>0 | при любом разбиении s мелкости |t|<d_E и любом выборе (.) xiÎ[xi-1,xi], I=1,…,it | å_I=1^itf(xi)Dx-I | <E При этом пишут I=lim s _t | t | ® 0. {T}Если ф-ция интегрируема на отр. [a,b] то она ограничина на этом отрезке {Док-во} Пусть ф-ция y=f(x) интегрируема на [a,b] но не является ограниченным. на этом отрезке. На этом отрезке рассмотрим произвольное разбиение t отрезка [a,b] то она ограничена хотя бы на одном на одном отр. разбиения. Пусть это будет отр.[x_j0-1,xj0] Тогда на этом отрезке существует последов-ть точек $ {xⁿ_jo}>0 | lim_n®¥f(xⁿ_jo)=¥ Рассмотрим сумму s_t=å_I=1^itf(xI)Dxi=f(xio)Dxjo +å_I=1^itf(x)Dxi=f(xjo)Dxjo+B Зафиксируем произвольным образом xiÎ[xi-1,xi] i¹jo lims_t(f,x1,…,x₀ⁿ,..,xit) =lim(f(xjo)Dxjo+B)=¥ m>0 существует n0 | s_t(f,x1,…,x_jo⁽ⁿ⁾,…,x_it)>m Отсюда Þ, что интегр сумма при мелкости разбеения |t|®0 не могут стремится ни к какому конечному результату. Предположим, что $ I=lim_|t|®0s_tÞ "E>0 $d_E>0 | "t, |t|<d_E и любой выбор точек xi вып-ся нер-во |d_t-I|<EÞ|d_t|=|d_t-I+I|<|d_t-I|+|I| <E+|I|; M=E+|I| при любом разбиении t в частности при при |t|<d_E можно выбрать точки x1,..,x_it такие, что |s_t|>M Þф-ция не может быть не ограничена на отр[a,b]. Ч.Т.Д. Ф-ла Ньтона-Лейбница _aò^bf(x)dx=Ф(b)-Ф(а)=Ф(х)|_а^b –(1) {T} (основная теорема интегрального исчисления) Пусть ф-ция y=f(x) непрерывна на [a,b] и Ф(х)-какая либо из её первообразных. Þ (1) {Док-во} F(x)= _aò^xf(t)dt тогда ф-ции F(x) и Ф(x) первообразные для f(x) на [a,b] $ F(x)=Ф(х)+С; _aò^xf(t)dt=Ф(х)+С Если x=a то _aò^аf(t)dt=0 Þ 0=Ф(а)+СÞ С=-Ф(а)Þ _aò^xf(t)dt=Ф(х)-Ф(а) Поллагая в равенстве x=b приходим к вормуле (1) Ч.Т.Д.

18. Равномерная сх-сть ф-ых послед-стей и рядов. Признак Вейерштрасса. Ф-циональную посл-сть {fn)x)} x Î E наз. равномерно сходящейся ф-цией f на м-ж Е, если для Î e >0, сущ номер N, такой, что для " т х Î E и " n >N вып-ся: |fn(x)-f(x)|<e. Если м-ж {fn)x)} равномерно сх-ся на м-ж Е, то она и просто сх-ся в ф-ции f на м-ж. Е тогда пишут: fn à f.

наз. равномерно сх-ся рядом, если на м-ж Е равномерно сх-ся посл-сть его частичной суммы., т. е. равномерная сх-сть ряда означает:Sn(x) à f(x) Не всякий сходящийся ряд является равномерно сх-ся, но всякий равномерно сх-ся – есть сх-ся Т. (Признак Вейерштрасса равномерной сх-ти ряда): Если числовой ряд: (7), где a >=0 сх-ся и для " x Î E и " n = 1,2… если выполняется нер-во un(x)|<=an(8), ряд (9) наз абс-но и равномерно сх-ся на м-ж Е.

Док-ва:

Абсолютная сх-сть в каждой т. х следует из неравенства (8) и сх-ти ряда (7). Пусть S(x) – сумма ряда (9), а Sn(x) – его частичная сумма.

Зафиксируем произвольное e >0 В силу сх-ти ряда (7) сущ. номера N, " n >N и вып. нерво . Следовательно: |S(x)-Sn(x)| = . Это означает, что Sn(x) à S(x) что означает равномерную сх-сть ряда..

19. Степенные ряды. Теорема Абеля. Степенным рядом наз ф-ный ряд вида: a₀+a₁x+a₂x²+… + a_nxⁿ =  (1) xÎR членами которого Степенным рядом наз также ряд: a₀+a₁(x-x0)+a₂(x-x0)²… + a_n(x-x0)ⁿ = 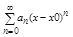(2) Степенной ряд (1) сх-ся абс-но по крайней мере в т. х = 0, а ряд (2) в т х = х0, т.е в этих случаях все кроме 1 равны 0. являются степенные ф-ции. Числа an Î R, наз коэффициентами ряда(1). Ряд (2) сводится к ряду (1) по ф-ле у = х-х0.Т Абеля: 1Если степенной ряд (1) сх-ся в т. х0 ¹ 0, то он сх-ся абсолютно при любом х, для которого |x|<|x0|, Если степеннгой ряд (1) расх-ся в т. х0, то он расх-ся в любой т. х, для которой |x|>|x0|

20. Радиус сх-ти и интервал сх-ти степенного ряда. Рассмотрим степенной ряд: (1) Число (конечное или бесконечное) R>=0 наз радиусом сх-ти ряда (1) если для любого х такого, что |x|<R ряд (1) сх-ся, а для " х таких. что |x|>R ряд расх-ся интервалом сх-ти. Т1 Для всякого степенного ряда (1) сущ-ет радиус сх-ти R 0<=R<=+¥ при этом, если |x|<R, то в этой т. х ряд сх-ся абс-но. Если вместо х взять у = х-х0, то получится: интервал сх-ти: |x-x0<R| будет: (x0-R, x0+R)При этом если |x-x0|<R, то ряд сх-ся в т. x абс-но иначе расх-ся. На концах интервала, т. е. при x = -R, x=+R для ряда (1) или x = x0-R, x=x0+R для ряда (3) вопрос о сх-ти решается индивидуально. У некоторых рядов интервал сх-ти может охватывать всю числовую прямую при R = +¥ или вырождаться в одну точку при R=0. Интервал на числовой оси состоящий из т. х для которых |x|<R, т. е. (-R, +R) наз. Т2 Если для степенного ряда (1) сущ-ет предел (конечный или бесконечный): , то радиус сх-ти будет равен этому пределу. Если сущ-ет предел степенного ряда, то радиус сх-ти равен 1/пределот ряда Если степенной ряд (1) имеет радиус сх-ти R>0, то на любом отрезке действительной оси вида |[-r,r] целиком лежащем внутри интервала сх-ти ряд (1) сх-ся равномерно.

На любом отрезке |x-x0|<=r сумма степенного ряда является непрерывной ф-цией.

Если ф-ция f(x) на интервале (x0-R, x0+R) является суммой ряда, то она дифференцируема на этом интервале и её производная f’(x) находится дифференцированием ряда. Степенной ряд можно почленно интегрировать на любом отрезке целиком принадлежащем интервалу сходимости при этом полученный степенной ряд имеет тот же радиус сходимости что и исходный ряд.

Поделиться:

Воспользуйтесь поиском по сайту: