 |
Общие сведения по КИХ-фильтрам
|
|
|
|
Содержание
Введение
Общие сведения по КИХ-фильтрам
Расчет цифрового фильтра
Модель цифрового фильтра и описание блоков модели
Моделирование работы цифрового фильтра в MatLab
Введение
С физической точки зрения цифровая фильтрация – это выделение в определенном частотном диапазоне с помощью цифровых методов полезного сигнала на фоне мешающих помех (рис. 1).
Рис. 1 Фильтрация помех с помощью цифрового ПФ.
По своим частотным свойствам фильтры делятся на:
– фильтры нижних частот (ФНЧ) – Low pass – рис.2а;
– фильтры верхних частот (ФВЧ) – High pass – рис.2б;
– полосовые фильтры (ПФ) – Band pass – рис.2в;
– режекторные фильтры (РФ) – Band stop – рис.2г.
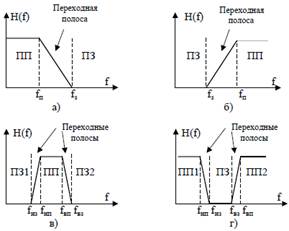
Рис. 2 Идеальные частотные характеристики фильтров.
На рис. 2 приняты следующие обозначения:
ПП – полоса пропускания – частотная область, внутри которой сигналы проходят через фильтр практически без затухания;
ПЗ – полоса задерживания – выбирается разработчиком такой, чтобы обеспечить затухание сигнала не хуже заданного;
Переходная полоса – частотная область между ПП и ПЗ (характеризуется скоростью спада, обычно выражается в дБ/декаду);
fп - частота среза полосы пропускания – точка на уровне 3дБ;
fз - частота среза полосы задерживания – определяется уровнем пульсаций ЧХ в ПЗ;
fнп, fвп – нижняя и верхняя частоты среза полосы пропускания;
fнз, fвз – нижняя и верхняя частоты среза полосы задерживания.
Частота среза в этом случае является условной границей между частотой среза полосы пропускания и частотой среза полосы задерживания.
АЧХ реальных фильтров (рис. 3, на примере ФНЧ) имеют пульсации в полосе пропускания δп и задерживания δз (нестабильность ЧХ в ПП и ПЗ). Часто в литературе они имеют другое название:
|
|
|
Rз – максимальное подавление в полосе задерживания, дБ;
Rп – минимальное подавление в полосе пропускания, дБ.
Пульсации ЧХ в ПП вносят определенные искажения в сигнал, поэтому они более значимы при определении параметров цифровых фильтров.
Рис. 3 Реальная АЧХ цифрового фильтра (на примере ФНЧ).
Математически работа цифрового фильтра во временной области описывается разностным уравнением:
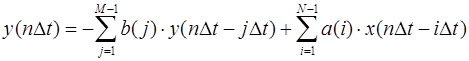, (1)
где 
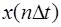и 
- 
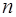- тые отсчеты входного и выходного сигналов фильтра, взятые через интервал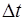 
; 
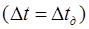и 
– постоянные коэффициенты цифрового фильтра.
Цифровые фильтры принято делить на два класса:
− нерекурсивные фильтры;
− рекурсивные фильтры.
Нерекурсивные фильтры называют еще фильтрами с конечной импульсной характеристикой (КИХ-фильтры), а рекурсивные фильтры - фильтрами с бесконечной импульсной характеристикой (БИХ-фильтры). В иностранной литературе их называют:
− FIR (Finite Impulse Response) – фильтр с конечной импульсной характеристикой;
− IIR (Infinite Impulse Response) – фильтр с бесконечной импульсной характеристикой.
Если в выражении (1) положить коэффициенты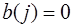 
, то фильтр, реализующий этот алгоритм, называется нерекурсивным. Его работа описывается уравнением:
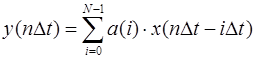, (2)
вычисляющим свертку двух последовательностей: коэффициентов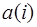 
и дискретных отсчетов входного сигнала 
.
Если хотя бы один коэффициент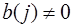 
, то фильтр, реализованный согласно выражения (1), называется рекурсивным. Очевидно, что БИХ-фильтр представляет собой устройство с обратной связью, а КИХ-фильтр - без обратной связи.
Общие сведения по КИХ-фильтрам
Нерекурсивные фильтры работают в соответствии с выражением (2). Раскроем сумму:
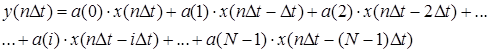(3)
КИХ-фильтр производит взвешенное суммирование (с коэффициентами 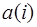) предшествующих отсчетов входного сигнала. Величину 
называют порядком фильтра, 
– шаг дискретизации. Структурная схема КИХ-фильтра представлена на рис. 4.
|
|
|
Рис. 4 Структурная схема КИХ-фильтра.
В этом фильтре дискретные выборки из сигнала 
, задержанные на интервалы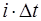 
, взвешиваются с коэффициентами 
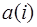и суммируются с образованием отклика 
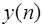. Фильтр, представленный на рис. 4 называют еще трансверсальным фильтром. Основными элементами фильтра являются:
− линия задержки с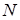 
отводами;
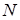− умножителей;
− многовходовый параллельный сумматор.
КИХ-фильтры всегда устойчивы. Форма частотной характеристики КИХ-фильтров слабо чувствительна к точности коэффициентов. Главным преимуществом КИХ-фильтра является линейность его ФЧХ.
Z - преобразование (3):
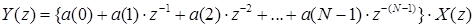. (4)
Тогда передаточная характеристика КИХ-фильтра:
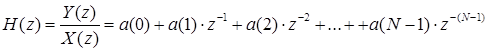. (5)
Если в (2.9) произвести замену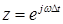 
, то ЧХ КИХ- фильтра будет иметь вид:
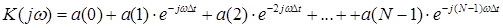. (6)
Из выражения (6) следует, что при заданном (фиксированном) шаге дискретизации можно реализовать самые разнообразные формы ЧХ цифрового фильтра, подбирая (рассчитывая) должным образом весовые коэффициенты .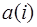
Расчет цифрового фильтра
Расчет цифрового фильтра будем проводить в пакете программ MatLab с помощью инструмента Filter Design & Analysis Tool.
После расчета цифрового фильтра в инструменте Filter Design & Analysis Tool получились значения для порядка фильтра, графики АЧХ и ФЧХ.
Порядок фильтра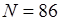 
.
Графики АЧХ в линейном и логарифмическом масштабах показаны на рис. 5 и рис 6 соответственно.
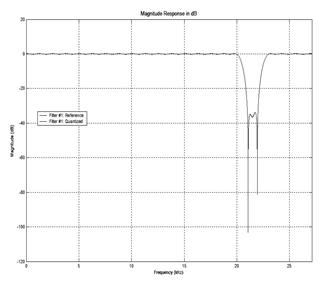
Рис. 5 График АЧХ в линейном масштабе.
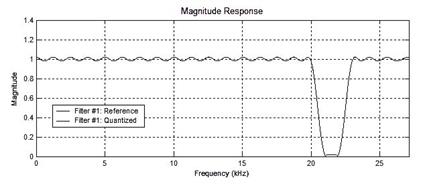
Рис. 6 График АЧХ в логарифмическом масштабе.
Графики АЧХ в логарифмическом масштабе и ФЧХ, где фаза измеряется в радианах, показаны на рис. 7.
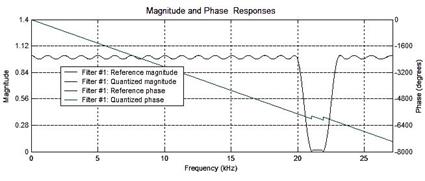
Рис. 7 Графики АЧХ и ФЧХ.
|
|
|
