Пример 4 - корреляция между индивидуальным и среднегрупповым профилями

Выборке петербуржцев в возрасте от 20 до 78 лет (31 мужчина, 46 женщин), уравновешенной по возрасту таким образом, что лица в возрасте старше 55 лет составляли в ней 50%[29], предлагалось ответить на вопрос: "Какой уровень развития каждого из перечисленных ниже качеств необходим для депутата Городского собрания Санкт-Петербурга?" (Сидоренко Е.В., Дерманова И.Б., Анисимова О.М., Витенберг Е.В., Шульга А.П., 1994). Оценка производилась по 10-балльной шкале. Параллельно с этим обследовалась выборка из депута­тов и кандидатов в депутаты в Городское собрание Санкт-Петербурга (n=14). Индивидуальная диагностика политических деятелей и претен­дентов производилась с помощью Оксфордской системы экспресс-видеодиагностики по тому же набору личностных качеств, который предъявлялся выборке избирателей.

В Табл. 6.6 представлены средние значения, полученные для ка­ждого из качеств в выборке избирателей ("эталонный ряд") и индиви­дуальные значения одного из депутатов Городского собрания.

Попытаемся определить, насколько индивидуальный профиль де­путата К-ва коррелирует с эталонным профилем.

Таблица 6.6

Усредненные эталонные оценки избирателей (п=77) и индивидуальные показатели депутата К-ва по 18 личностным качествам экспресс-видеодиагностики

Наименование качества	Усредненные эталонные оценки избирателей	Индивидуальные показатели депутата К-ва
1. Общий уровень культуры	8,64
2. Обучаемость	7,89
3. Логика	8,38
4. Способность к творчеству нового	6,97
5.. Самокритичность	8,28
6. Ответственность	9,56
7. Самостоятельность	8,12
8. Энергия, активность	8,41
9. Целеустремленность	8,00
10. Выдержка, самообладание	8,71
И. Стойкость	7,74
12. Личностная зрелость	8,10
13. Порядочность	9,02
14. Гуманизм	7.89
15. Умение общаться с людьми	8,74
16. Терпимость к чужому мнению	7.84
17. Гибкость поведения	7,67
18. Способность производить благоприятное впечатление	7,23

Таблица 6.7

Расчет d² для рангового коэффициента корреляции Спирмена между эталонным и индивидуальным профилями личностных качеств депутата

Наименование качества	Ряд 1: ранг качества в эталонном профиле	Ряд 2: ранг качества в индивидуальном профиле	d	d2
1 Ответственность			-1
2 Порядочность		8,5	-6,5	42,25
3 Умение общаться с людьми		13,5	-10,5	110,25
4 Выдержка, самообладание			-8
5 Общий уровень культуры
6 Энергия, активность
7 Логика		8,5	-1,5	2,25
8 Самокритичность
9 Самостоятельность
10 Личностная зрелость
И Целеустремленность	И
12 Обучаемость	12,5		-2,5	6,25
13 Гуманизм	12,5	И	1,5	2,25
14 Терпимость к чужому мнению			-2
15 Стойкость
16 Гибкость поведения			-2
17 Способность производить благоприятное впечатление		13,5	3,5	12,25
18 Способность к творчеству нового	18.
Суммы				487,5

Как видно из Табл. 6.6, оценки избирателей и индивидуальные показатели депутата варьируют в разных диапазонах. Действительно оценки избирателей были получены по 10-балльной шкале, а индивидуальные показатели по экспресс-видеодиагностике измеряются по 20-ти балльной шкале. Ранжирование позволяет нам перевести обе шкалы измерения в единую шкалу, где единицей измерения будет 1 ранг, а максимальное значение составит 18 рангов.

Ранжирование, как мы помним, необходимо произвести отдельно по каждому ряду значений. В данном случае целесообразно начислять большему значению меньший ранг, чтобы сразу можно было увидеть, на каком месте по значимости (для избирателей) или по выраженности (у депутата) находится то или иное качество.

Результаты ранжирования представлены в Табл. 6.7. Качества перечислены в последовательности, отражающей эталонный профиль.

Сформулируем гипотезы.

H₀: Корреляция между индивидуальным профилем депутата К-ва и эталонным профилем, построенным по оценкам избирателей, не от­личается от нуля.

H₁: Корреляция между индивидуальным профилем депутата К-ва и эталонным профилем, построенным по оценкам избирателей, стати­стически значимо отличается от нуля. Поскольку в обоих сопоставляемых ранговых рядах присутствуют

группы одинаковых рангов, перед подсчетом коэффициента ранговой

корреляции необходимо внести поправки на одинаковые ранги Т_а и Т_b:

где а - объем каждой группы одинаковых рангов в ранговом ряду А,

b - объем каждой группы одинаковых рангов в ранговом ряду В.

В данном случае, в ряду А (эталонный профиль) присутствует одна группа одинаковых рангов - качества "обучаемость" и "гуманизм" имеют один и тот же ранг 12,5; следовательно, а =2.

T_а=(2³-2)/12=0,50.

В ряду В (индивидуальный профиль) присутствует две группы одинаковых рангов, при этом b₁=2 и b₂=2.

T_a=[(2³-2)+(2³-2)]/12=1,00

Для подсчета эмпирического значения r_s используем формулу

В данном случае:

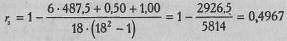
Заметим, что если бы поправка на одинаковые ранги нами не вносилась, то величина r_s была бы лишь на (на 0,0002) выше:

При больших количествах одинаковых рангов изменения г₅ могут оказаться гораздо более существенными. Наличие одинаковых рангов означает меньшую степень дифференцированное™ упорядоченных переменных и, следовательно, меньшую возможность оценить степень связи между ними (Суходольский Г.В., 1972, с.76).

По Табл. XVI Приложения 1 определяем критические значения г, при N=18:

Ответ: Hq отвергается. Корреляция между индивидуальным профилем депутата К-ва и эталонным профилем, отвечающим требова­ниям избирателей, статистически значима (р<0,05) и является положи­тельной.

Из Табл. 6.7 видно, что депутат К-в имеет более низкий ранг по шкалам Умения общаться с людьми и более высокие ранги по шкалам Целеустремленности и Стойкости, чем это предписывается избиратель­ским эталоном. Этими расхождениями, главным образом, и объясняется некоторое снижение полученного r_s.

Сформулируем общий алгоритм подсчета r_s.

АЛГОРИТМ 20

Расчет коэффициента ранговой корреляции Спирмена r_s.

1. Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные А и В.

2. Проранжировать значения переменной А, начисляя ранг 1 наимень­шему значению, в соответствии с правилами ранжирования (см. п.2.3). Занести ранги в первый столбец таблицы по порядку номе­ров испытуемых или признаков.

3. Проранжировать значения переменной В, в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.

4. Подсчитать разности d между рангами А и В по каждой строке таблицы и занести в третий столбец таблицы.

5. Возвести каждую разность в квадрат: d². Эти значения занести в четвертый столбец таблицы.

6. Подсчитать сумму квадратов ∑ d ².

7. При наличии одинаковых рангов рассчитать поправки:

где а - объем каждой группы одинаковых рангов в ранговом ряду А;

b - объем каждой группы одинаковых рангов в ранговом ряду В.

8. Рассчитать коэффициент ранговой корреляции г₅ по формуле:

а) при отсутствии одинаковых рангов

б) при наличии одинаковых рангов

где ∑ d ² - сумма квадратов разностей между рангами*

Т_а и T_b, - поправки на одинаковые ранги;

N - количество испытуемых или признаков, участвовавших в ранжировании.

9. Определить по Табл. XVI Приложения 1 критические значения г_s для данного N. Если r_s превышает критическое значение или по крайней мере равен ему, корреляция достоверно отличается от 0.

 

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: