Применение критерия Н Крускала-Уоллиса для решения задачи 3

Вначале сформулируем гипотезы.

H₀: Четыре возрастные группы испытуемых-руководителей промышлен­ного предприятия не различаются по уровню фактора N из 16PF¹.

H₁: Четыре возрастные группы испытуемых-руководителей промышлен­ного предприятия различаются по уровню фактора N из 16PF.

В Табл. 9.4 реализованы первые шаги алгоритма в подсчете критерия Н.

^{_________________}

¹ 16PF - принятое в иностранной н отечественной литературе сокращение для обо­значения 16-факторного личностного опросника Р.Б. Кеттелла.

 

 

Таблица 9.4

Подсчет ранговых сумм по четырем возрастным группам испытуемых по фактору N из 16PF (N=28)

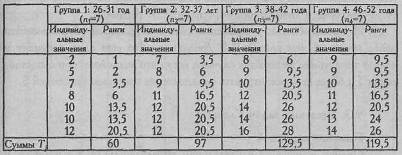
Проверим, совпадает ли общая сумма рангов с расчетной величиной:

Суммы равны, мы можем переходить к расчету эмпирического значения Н. Все расчеты будем выполнять с точностью до сотых долей единицы.

Поскольку сопоставляется 4 группы испытуемых, а не 3, мы не можем воспользоваться специальной таблицей для критерия Н и долж­ны обратиться к Табл. IX Приложения 1 для определения критических значений критерия χ ²_r. Для этого определим количество степеней свобо­ды для данного количества групп (с =4):

v = c – 1=4 – 1=3

H_эмп< χ ²_кр.

Ответ: H₀принимается. Четыре возрастные группы руководи­телей промышленного предприятия не различаются по уровню фактора N 16-факторного личностного опросника Р.Б. Кеттелла.

Итак, мы смогли убедиться в том, что критерий Н оказывается менее мощным, чем критерий S Джонкира. Это еще один аргумент впользу того, чтобы во всех тех случаях, когда это возможно, при сопостав­лении 3 и более выборок отдавать предпочтение критерию тенденций S.

Решения задач Главы 3

Решение задачи 4

Оценки отношения к наказаниям определены для 3-х условий, и вопрос задачи требует проверки достоверности тенденции в оценках. Целесообразнее всего было бы использовать критерий тенденций L Пейджа, но количество испытуемых п=16, а критические значения кри­терия L определены только для n ≤12. Используем вначале критерий Фридмана, а затем все же попробуем использовать критерий L, разде­лив выборку на 2 части.

Решение задачи с использованием критерия χ ²_r Фридмана

Сформулируем гипотезы:

H₀: Испытуемые примерно в одинаковой степени оправдывают (признают возможными) телесные наказания, которые их ребенок может получить от них самих, от бабушки и от воспитательницы (или учительницы).

H₁: Испытуемые в разной степени оправдывают телесные наказания; которые их ребенок может получить от них самих, от бабушки и от воспитательницы (или учительницы).

Проранжируем оценки каждого испытуемого по трем условиям. Ранжирование производится по строкам, при этом меньшая оценка по­лучает меньший ранг, большая оценка - наибольший ранг (Табл. 9.5).

 

Таблица 9.5

Оценки допустимости телесных наказаний со стороны разных людей и их ранги (n =16)

Испытуемые	Условие 1: "Я сам"	Условие 2: "Бабушка"	Условие 3: "Учительница"
Оценка	Ранг	Оценка	Ранг	Оценка	Ранг
				1.5		1.5
		2.5		2.5
		2.5		2.5
		2,5		2.5
		2,5		2,5
		2,5		2,5
		2.5		2.5
Суммы				34,5		19,5
Средние	4.44	3,75	2,50

Как видно из Табл. 9.5, суммы рангов по каждому условию со­ставляют: 42; 34,5; 19,5, что в сумме равняется 96.

Расчетная сумма рангов:

Реально полученная и расчетная суммы совпадают, мы можем переходить к дальнейшим расчетам.

Определим эмпирическое значение χ ²_r:

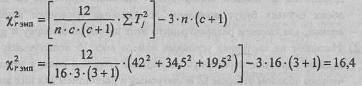
В нашем случае количество условий с =3, однако п>9, поэтому мы не можем воспользоваться таблицами, специально рассчитанными для критерия χ ²_r. Нам придется сопоставлять полученное эмпирическое значение с критическими значениями критерия χ ²_r. Число степеней сво­боды определяем по формуле:

v = c –1=3–1=2.

По Табл. IX Приложения 1 определяем критические значения для v =2:

Ответ: H₀ отклоняется. Принимается H_1. Испытуемые в раз­ной степени оправдывают телесные наказания, которые их ребенок может получить от них самих, от бабушки и от воспитательницы (учительницы).

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: