Вторая матрёшка. Линии на высоту.

На пути подсчёта линий нас подстерегают две опасности.

Первая - формальная. Почему-то общепринято считать вертикальное и горизонтальное разрешения. Однако из-за структуры матрицы (расположения пикселей) оказывается, что диагональное примерно в 1,4 раза больше. Этим поспешила воспользоваться одна известная фирма, которая просто повернула матрицу на 45 градусов и назвала модным словом "Супер ЦЦД". С 3 миллионов сенсоров электроника камеры интерполировала 6-мпиксельную картинку. Скептики тут же принялись мерить разрешение своими мирами и с удивлением обнаруживали что таки-да, "дед Мороз существует" - матрица на уровне 5-6мегапиксельных "обычных". Но никто не догадался повернуть миру под 45 градусов - тогда всё станет на свои места - разрешение "обычных" увеличится, а "супер" - снизится, и хвалёные 6 мегапикселей будут на уровне полутора "обычных". А поскольку в реальной жизни редко встречаются ровные параллельные линии, то в среднем разрешение как было на уровне 3-амегапиксельных, так и осталось, что блестяще подтверждается тем фактом, что многие владельцы "волшебных" камер, поиграв с интерполированным разрешением, вернулись на стандартное 3Мп для экономии места на флеш-карте, т.к. не заметили явных улучшений.

Вторая опасность - принципиальная и связана с размытостью понятия "линии различимы". На словах всё выглядит достаточно гладко и понятно. В реальности выясняется, что

• "различимость" линий не дискретна (различимы - неразличимы), а непрерывна - (различимы хорошо, не очень, плохо, очень плохо и т.п.). На самом деле просто плавно падает контраст с единицы до нуля. Поэтому разные наблюдатели видят переход от "плохо различимы" к "практически не различимы" в РАЗНЫХ местах. Этот эффект не зависит от фотосистемы и наблюдается и в плёночной фотографии.
• в цифровой фотографии кроме этого из-за структуры матрицы добавляются цветные разводы, муар и даже "греческий орнамент", что ещё более усложняет процесс визуального тестирования.

На иллюстрации приведён типичный (не самый сложный) пример. В зависимости от "строгости" наблюдателя колебания разрешения легко достигают 20-40%. В результате ценность цифр, приводимых в обзорах, становится сомнительной. Как мы видели из предыдущей таблицы, максимальные цифры для 3Мп и 5Мп отличаются всего лишь на 30%, поэтому 20-40% - это катастрофически много.

Лирическое отступление.
Похожая ситуация складывается с другими "паспортными" параметрами бытовой техники - например мощностью и частотным диапазоном недорогих аудиосистем. Мощность можно измерять при разных значениях искажений, а нижнюю границу частотного диапазона - при разном падении АЧХ, чем изготовители активно пользуются. В результате мы часто видим пластиковые компьютерные колонки за 50уе с диапазоном от 40Гц и качественные HiFi колонки за 600 уе с диапазоном от 45Гц. Угадайте, у кого из них басы глубже на самом деле?

Аналогия с акустикой не случайна. Действительно, если принять звуковое давление на средних частотах за единицу ("нормировка АЧХ"), то с понижением частоты оно будет плавно падать до нуля и обычно нижней границей называют ту частоту, при которой давление равно либо 0,5, либо 0,25, либо 0,1 (в зависимости от методики, соответственно и результаты - разные). При этом сама АЧХ(Амплитудно-Частотная Характеристика) достаточно объективна и даёт гораздо бОльшее представление чем сухая цифра "границы". Нельзя ли и в оптике вместо "границы" разрешения снять плавную кривую падения контраста при росте частоты штрихов? Именно эта кривая и получила название Modular Transfer Function (MTF) - функция передачи модуляции. Более подробно (на английском) можно почитать здесь, а кратко я изложу ниже. Итак, если вместо "классических" штрихов с прямоугольным графиком яркости использовать "синусоидальные", а функцию "контраста" от частоты определить как (Iw-Ib)/(Iw+Ib), где Iw и Ib - яркости изображений "самой белой" и "самой тёмной" точки на данной частоте линий, то MTF(частоты)=КОНТРАСТ(частоты)/КОНТРАСТ(низкой частоты). Таким образом, на низкой частоте MTF равна единице, а с ростом плавно падает до нуля (когда изображения линий сливаются, контраст становится нулевым). Классически определяемое "разрешение" соответствует частоте, при которой MTF становится равной примерно 0,1.

Как и АЧХ в акустике, MTF способна дать гораздо больше информации. Так, два объектива, имеющие одинаковое разрешение (скажем, 1600lph) могут иметь разные графики MTF - у одного график опускается сразу от 50lph вниз, плавно достигая 0,1 при 1600 lph, а у другого держится возле 0,95 "до последнего", и лишь начиная с 1200lph круто падает вниз. При частоте 800-1000lph у первого будет MTF 0,25, а у второго - 0,95. В результате снимки первого будут заметно более вялыми ("мыльными"). Тем не менее формальное разрешение у них действительно одинаково.

Ну уж теперь-то, кажется, всё строго. Измеряем MTF, публикуем сравнение графиков и строим аппараты по ранжиру... Но не будем торопиться. Всё опять не так просто.

Третья матрёшка. MTF.
Измерения и влияние шарпенинга.

Измерить MTF можно даже в домашних условиях. Для этого потребуется всего лишь струйный принтер (720dpi и выше), несколько листов фирменной "струйной" бумаги, а также несколько небольших бесплатных программ, скачанных из Сети. Как это всё сделать, подробно описано у меня в статье Измеряем MTF самостоятельно. В частности, я снимал графики для нескольких объективов к Canon D60. Результаты для угла кадра представлены ниже (линии на высоту кадра можно получить умножением цифр на оси Х примерно на 30, график просто в привычных "плёночных" координатах):

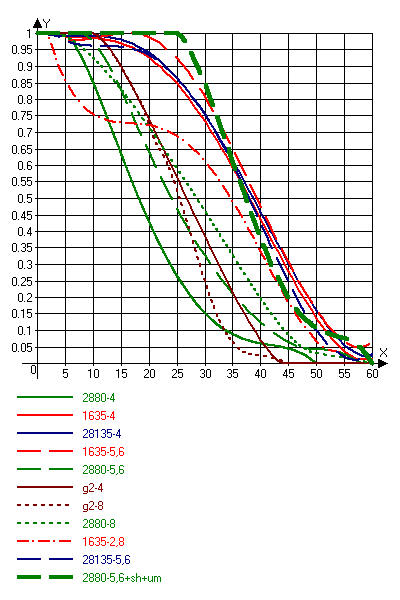
Подробное обсуждение этих графиков есть по упомянутой ссылке, нас же здесь интересует сравнение красных и зелёных линий. Красные принадлежат профессиональному объективу 16-35mm/2.8L стоимостью под полторы тысячи долларов. Зелёные - наидешевейшему, наибюджетнейшему пластмассовому 28-80mm/3,5-5,6 за 100 долларов. Если сравнивать тонкие линии - всё логично и "L-ка" оставляет бюджетник далеко позади. Но взгляните на толстый зелёный пунктир! Он отличается от остальных "всего лишь" другими (+1деление) установками шарпенинга на камере (на самом деле - в RAW-конверторе, но это одно и то же) и очень умеренным шарпенингом в Фотошопе (ещё грубо говоря "1 деление"). Но в результате он полностью догнал L-ку! (Понятно, что если применить шарп к L-ке она вновь всех "сделает", но речь сейчас о другом!)

Мы подошли к ключевому моменту. Поставьте себя на место производителя фотокамеры. У Вас есть два пути увеличения разрешения - сделать замечательный резкий объектив уровня L-оптики (+500-1000долларов к цене камеры в зависимости от размера матрицы) или просто "перешить" в её процессоре уровень шарпенинга на одно-два "деления" в большую сторону (бесплатно!!!). Как Вы думаете, что выбирают реальные производители? Разумеется шарпенинг! В результате увеличиваются шумы и понижается реальная чувствительность (если её определять как значение при фиксированном уровне шума). Но это никого не волнует, потому что уровень шума измерять толком не научились, в обзорах он фигурирует редко, а вот высокое разрешение (вместе с мегапикселями и зумом) - сильный маркетинговый козырь. Косвенное подтверждение тому - наличие ISO400 и даже иногда ISO800(!) в камерах с матрицами 1/2,5"! Что мы имеем ещё плохого от "встроенного" шарпенинга, кроме увеличения шумов? Мы имеем, образно говоря, "потолок" детализации. Т.е. дальнейший шарпенинг в Фотошопе больше не приводит к её увеличению без сопутствующих артефактов и искажений, "несовместимых с жизнью", в отличие от камер без встроенного шарпа. Там с помощью Фотошопа иногда можно вполне "догнать" разрешение до "накачанных" лидеров (разумеется ценой того же шума, но у нас по крайней мере есть выбор!).