 |
Задача о выборе наиболее экономного маршрута доставки груза.
|
|
|
|
Основы динамического программирования
Понятие о ДП. Принцип оптимальности
ДП – это решение задач математического программирования, которые м.б. представлены в виде многошагового (многоэтапного) процесса.
Стратегия – последовательность взаимосвязанных решений.
Оптимальная стратегия – стратегия, обеспечивающая получение наилучшего результата с т. зр. заранее выбранного критерия.
Принцип оптимальности: оптимальная стратегия обладает тем свойством, что каковы бы ни были первоначальное состояние и решение, принятое в начальный момент, последующие решения должны составлять оптимальную стратегию относительно состояния, являющегося результатом первоначального решения.
Условно - оптимальным называется решение, найденное при условии, что последующий шаг закончился определенным образом, т.е. принятие решений в обратном направлении (от конца к началу).
Безусловная оптимизация – принятие решений в прямом направлении (от начала к концу).
Общая постановка задачи ДП
Рассмотрим некоторый развивающийся во времени управляемый процесс, т.е. такой, на развитие которого можно влиять принимаемыми решениями (изменение состава оборудования, изменение объёмов поставок сырья и т.п.).
Предполагается, что процесс распадается на N шагов (этапов).
Состояние процесса на начало каждого шага будем характеризовать вектором состояния s i = (si 1; …; sim).
Множество всех состояний, в которых может находиться процесс на начало i -го шага, обозначим через Si.
Начальное состояние процесса считается известным, т.е. вектор s о задан.
Развитие процесса заключается в последовательном переходе из одного состояния в другое.
|
|
|
Если процесс находится в состоянии s i, то состояние s i +1 на следующем шаге определяется не только вектором s i, но и решением u i, принятым на i -м шаге:
s i +1 = φ(s i; u i).
Решение на каждом шаге выбирают из некоторого множества Ui возможных решений.
Развитие процесса описывают последовательностью состояний s 0; s 1; …; s N -1; s N, где s i ϵ Si.
Стратегия –это любая последовательность u 0; u 1; …; u N -1 допустимых решений, переводящую процесс из начального состояния s 0 в конечное s N.
Каждой стратегии надо сопоставить некоторую оценку – значение целевой функции fN (s).
Зададим целевую функцию в виде суммы оценочных функций ri (s i; s i +1), значения которых получаются на каждом шаге процесса при переходе из состояния s i в состояние s i +1, т.е.

Многошаговый процесс полностью описан, если заданы: допустимое множество состояний Si, допустимое множество решений Ui, правило перехода из одного состояния в другое под воздействием выбранного решения, целевая функция.
Формулировка общей задачи динамического программирования (ОЗДП):
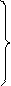
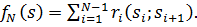
при условиях (1)
s 0 – вектор начального состояния процесса,
s i +1 = φ(s i; u i), s i ϵ Si, u i ϵ Ui (i = 0, …, N -1).
Пример.
Задача о выборе наиболее экономного маршрута доставки груза.
На данной сети дорог имеется несколько маршрутов, по которым можно доставлять груз из пункта 1 в пункт 10 (рис. 1).
Рисунок 1 – Граф перевозки грузов
Известны стоимости перевозки единицы груза между отдельными промежуточными пунктами сети (они проставлены на сети у соответствующих рёбер).
Требуется в системе дорог выбрать маршрут доставки груза из пункта 1 в пункт 10, которому соответствуют наименьшие затраты.
Дл решения задачи методом ДП разобьём все пункты сети на группы (табл. 1)
Таблица 1
| I | II | III | IV | V |
К группе I отнесём пункт 1, к группе II – пункты, в которые можно попасть непосредственно из пункта 1 (таковыми будут 2; 3; 4), к группе III отнесём пункты, в которые можно попасть непосредственно из любого пункта группы II (таковыми будут 5; 6; 7), и т.д.
|
|
|
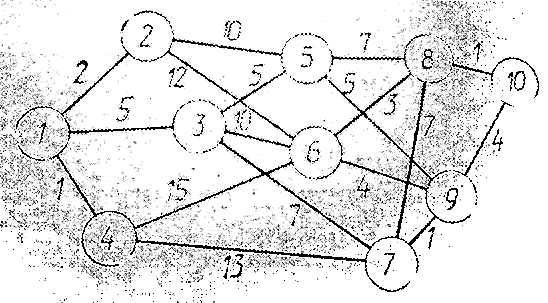
Рисунок 2
В результате движения транспорта с грузом из пункта 1 в пункт 10 примет поэтапный характер: на первом этапе транспорт перемещается из пункта 1 в какой-то пункт II, на втором этапе – из пункта группы II в пункт группы III и т.д.
Вместе с этим и процесс нахождения наиболее экономного маршрута из пункта 1 в пункт 10 распадается на шаги.
На каждом шаге надо так выбрать маршрут следования груза в пункт соседней группы, чтобы затраты были минимальны.
После разбиения на группы, пункты, оказавшиеся в одной и той же группе, дорогами не соединены.
Принцип оптимальности, применительно к рассматриваемой задаче: оптимальный маршрут доставки груза из пункта 1 в пункт 10 обладает тем свойством, что, каков бы ни был маршрут достижения некоторого промежуточного пункта сети, дальнейший маршрут следования должен совпадать с оптимальным маршрутом для части маршрута, начинающейся с этого пункта.
В данном случае процесс состоит из четырёх шагов (рис. 2).

Рисунок 2
Будем оптимизировать каждый шаг, начиная с последнего – четвёртого.
На этом шаге в пункт 10 можно попасть из пункта 8 или 9, причём из каждого пункта только одним способом.
Если предпоследний, третий шаг, привёл груз в пункт 8, то дальше следует двигаться по маршруту 8-10, и затраты на перевозку единицы груза будут равны единице; если же в пункт 9 – то следует двигаться по маршруту 9-10, на котором затраты составят 4 единицы.
Условное оптимальное решение помечаем на сети стрелкой, выходящей из соответствующего кружка, а величину затрат записываем в нижней половинке кружка.
Переходим к оптимизации предпоследнего, третьего шага.
Для этого рассмотрим все возможные исходы предшествующего, второго шага.
После этого шага груз может оказаться только в одном из пунктов – 5, 6, 7.
Для каждого пункта выбираем условное оптимальное решение – оптимальный маршрут в пункт 10 и соответствующие минимальные затраты.
Так, если груз оказался в пункте 5, то далее можно следовать либо через пункт 8, либо через пункт 9.
|
|
|
В первом случае затраты равны 7+1=8 единицам, во втором – 5+4=9 единицам.
Значит, условный оптимальный маршрут из пункта 5 в пункт 10 проходит через пункт 8, а условные оптимальные затраты составляют 8 единиц.
На ребре 5-8 сети ставим стрелку, а в кружке 5 записывам минимальные затраты: 8=7+1.
Ребро 5-9 остаётся без стрелки.
Аналогично для пункта 6 находим условно-оптимальный маршрут 6-8-10 с затратами в 4 единицы; для пункта 7 – условно-оптимальный маршрут 7-9-10 с затратами в 5 единиц.
Далее оптимизируем путь доставки груза на втором шаге процесса.
Для этого рассматриваем все возможные исходы первого шага.
После первого шага груз мог оказаться только в одном из пунктов: 2, 3 или 4.
При нахождении условного оптимального решения в каждом из этих пунктов надо просмотреть все возможные маршруты из этого пункта и для каждого из них найти сумму затрат на этом шаге и условных минимальных затрат на оптимальном продолжении маршрута, уже построенном для следующего пункта.
Этого требует принцип оптимальности.
Из всех возможных маршрутов выбирается тот, для которого эта сумма меньше (если суммы равны, выбирается любой маршрут).
Для пункта 2 оптимальным будет маршрут 2-6-8-10 с затратами 12+4=16 единиц; для пункта 3 – маршрут 3-7-9-10 с затратами 7+5=12 единиц; для пункта 4 – маршрут 4-7-9-10 с затратами 13+5=18 единиц.
Оптимизируем, наконец, первый шаг.
Для выбора условного оптимального решения рассматриваем три возможных маршрута: через пункты 2, 3 или 4.
Устанавливаем, что наивыгоднейшим будет маршрут 1-3 с затратами в 17 единиц.
Итак, этап условной оптимизации закончен, и остаётся пройти процесс в направлении от пункта 1 к пункту 10 и прочитать оптимальный маршрут: 1-3-7-9-10.
Заметим, что на первом этапе нами выбран маршрут 1-3 доставки груза, по которому затраты в 2,5 раза превышают затраты на маршруте 1-2 и в 5 раз на маршруте 1-4.
Оказалось, что с т.зр. всего четырёхэтапного маршрута, а не донного первого этапа, следует пойти на «жертву» на первом этапе с тем, чтобы минимизировать общие затраты на всём четырёхэтапном маршруте.
|
|
|
Это иллюстрирует одну из главных особенностей метода: выбирать решение на каждом шаге, руководствуясь не выгодой, получаемой на данном шаге, а общей выгодой, получаемой по окончании всего процесса.
Применённый метод рассуждения не только позволил найти оптимальный маршрут доставки груза из пункта 1 в пункт 10, но и всю структуру оптимальных маршрутов относительно пункта 10 для данной сети дорог.
Например, наиболее экономный маршрут доставки груза из пункта 4 в пункт 10 пройдёт через пункты 7 и 9.
Этот факт для практических нужд часто более ценен, чем нахождение только одного оптимального маршрута (рис. 3).
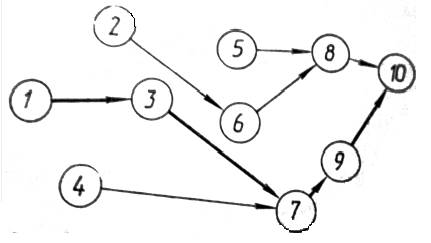
Рисунок 3
|
|
|


