Динамические методы измерений силы тяжести

1. Маятниковый метод получил наиболее широкое распространение среди других динамических методов, применялся на практике в течение почти двух столетий и был доведен до высокой степени совершенства.

Маятником можно считать любое твердое тело, совершающее свободные колебания относительно горизонтальной оси. В теории метода рассматривают математический и физический маятники. Математический маятник представляет собой материальную точку с массой m, подвешенную на абсолютно нерастяжимой и невесомой нити длиной ℓ (рис. 1.2.)

Угол φ₀ соответствует максимальному отклонению маятника от положения равновесия и называется амплитудой колебаний. Врем, необходимое маятнику для прохождения от одного крайнего положения +φ₀ до другого крайнего положения –φ₀, называется периодом колебаний Т маятника. Дифференциальное уравнение движения математического маятника имеет вид:

d²φ/dt² = - (g/ℓ) sin φ (1.7)

Решение этого уравнения дается в виде:

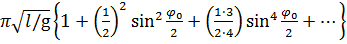(1.8.)

Как видно из последнего равенства, период зависит от амплитуды. При малых амплитудах, когда можно считать sinφ = φ, период колебаний маятника не зависит от амплитуды (это свойство маятника называется изохронностью) и равенство (2.37) приобретает вид формулы Гюйгенса:

(1.9.)

Обычно при гравиметрических измерениях амплитуда колебаний маятника не превышает 1^o, поэтому условие sinφ = φ практически выполняется и из формулы (1.9.) получим:

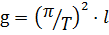(1.10.)

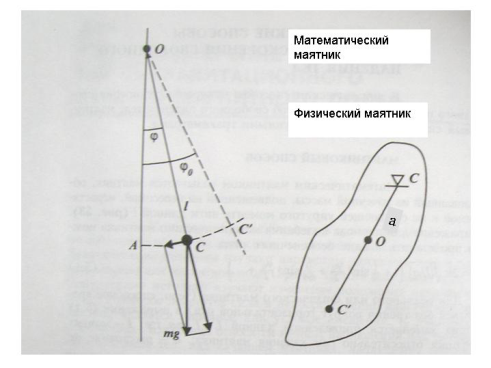
Рис. 1.2. Математический и физический маятники.

На практике осуществить математический маятник с необходимой степенью точности невозможно. Поэтому при измерениях силы тяжести используют физический маятник, который, имея определенные размеры, не является точечным и нить подвеса не является абсолютно нерастяжимой и невесомой. Уравнение движения физического маятника можно записать так:

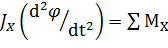(1.11)

где J_X и M_X — соответственно момент инерции и момент сил относительно оси вращения Х.

Поскольку сумма моментов действующих сил:

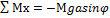, где М – масса тела, то уравнение движения принимает вид: 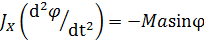(1.12.)

или 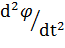= (1.13.)

где l = 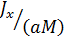(1.14.)

Выражение (1.14.) совпадает с дифференциальным уравнением колебания математического маятника, т. е. физический маятник колеблется по тем же законам, что и математический, но роль длины l для него играет величина J_X/(aM), называемая приведенной длиной физического маятника.

Обычно приведенную длину физического маятника трудно определить с достаточной точностью, например, для маятника с приведенной длиной l = 100 см (Т ≈ 1с) при заданной погрешности измерения ускорения силы тяжести 0,1 мГл период колебаний и длину надо измерять с допустимыми погрешностями соответственно 3,5 10^-8 с и 0,07 мкм. Поэтому для определения абсолютных значений g использовали специальные оборотные маятники. Абсолютное значение силы тяжести необходимо знать хотя бы в одной точке. В настоящее время таким пунктом является Потсдамский геодезический институт, к которому отнесены все гравиметрические съемки мира. Здесь определение абсолютного значения силы тяжести было проведено под руководством Гельмерта в 1898 -1904 г.г. На основании 192 определений получено абсолютное значение силы тяжести 981 274 ±3 мГл.

При современном состоянии техники точность этого метода не может быть повышена из-за ряда трудно учитываемых факторов: удлинения маятника под действием собственного веса, деформации опор, неточности измерения приведенной длины и др. Маятниковым методом проводили и относительные измерения (если в одном из пунктов известно полное значение силы тяжести g₁). В последнем случае, если измерить периоды качания маятника в двух пунктах Т₁ и Т₂, то, учитывая формулу (1.10):

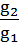= , откуда следует (1.15)

Гравиметры для относительных измерений силы тяжести применялись для создания опорных гравиметрических сетей и обеспечивали погрешности определения относительных значений силы тяжести около 0,1 мГл при весе порядка 90 кг и цикле одного измерения 15 –20 мин. Однако в последнее время они были вытеснены приборами, основанными на баллистическом способе измерений.

2. Баллистический метод основан на зависимости времени падения тел в вакууме (t) от значения силы тяжести (g):

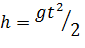, откуда 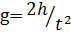(1.16.)

где h - высота, с которой падает объект при нулевой начальной скорости.

Из-за требований высокой точности определения величин h и t, только в 60-х годах 20 века, с применением лазерной техники, появилась возможность конструировать приборы для измерения силы тяжести этим методом. Кроме того, как было установлено, величины h и t нельзя отсчитывать от начала падения, так как при освобождении тело может получить дополнительное ускорение. Наиболее приемлемым оказалось бросать тело вверх и измерять время, за которое тело проходит определенный участок пути при подъеме и падении.

В этом случае формула для расчета значения g достаточно проста:

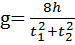, (1.17)

где t ₁ и t₂ - промежутки времени между пересечениями телом специальных щелей при движении его вверх и вниз. В различных странах за рубежом разработаны и применяются несколько типов баллистических гравиметров. Почти все они представляют собой экспериментальные образцы. В Сибирском отделении АН РФ разработан баллистический гравиметр, в котором применяется интерферометр Майкельсона с газовым лазером (рис. 1.3.). В вакуумной камере 1 падает уголковый отражатель 2, ориентируемый по вертикали в крайнем верхнем положении при помощи агатовой опоры. Оптическая система интерферометра содержит стабилизированный лазер 3, коллиматор 4. полупрозрачные зеркала 5, делящие луч на две части, и фотоумножитель 6. В счетном блоке осуществляется измерение пути и времени. Величина h определяется по числу интерференционных полос, образованных при наложении прямого и обратного луча лазера от падающего уголкового отражателя. Для обработки результатов используется компьютер. 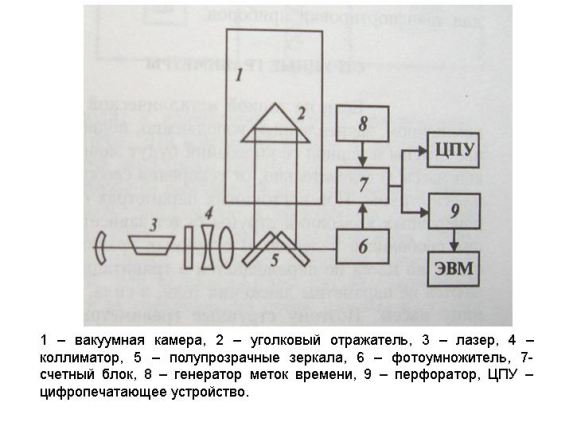Рис. 1.3. Схема баллистического интерферометра для определения абсолютных значений силы тяжести.

Один цикл измерения – подъем и падение уголкового отражателя, а также обработка результата – занимает около 12 с. За один час, включая паузы, можно сделать около 200 циклов. За несколько часов может быть достигнута точность в несколько сотых мГл. Для достижения точности выше 0,01 мГл наблюдения ведутся сутками. Полный комплект установки имеет массу в несколько сотен килограммов, но разделяется на отдельные транспортабельные части. Баллистические гравиметры-интерферометры используются сейчас для геодезических измерений и для создания опорных гравиметрических сетей.

3. Струнный метод основан на измерениях собственных поперечных колебаний струны, натянутой грузом. Если подвесить массу на тонкой металлической нити (струне), то натяжение струны и соответственно период колебаний будут зависеть от веса массы, длины и веса струны. При постоянных параметрах струны и груза изменения силы тяжести проявляются в изменении частоты колебаний струны.

Частота колебаний (f) идеально гибкой струны определяется:

f= 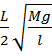, (1.18)

где L - длина струны, M - масса груза, подвешенного на струне, l - линейная плотность струны (г/см). Отсюда:

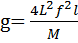. (1.19.)

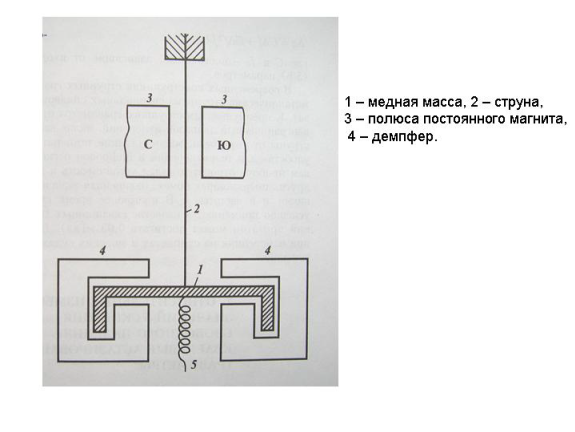
Рис. 1.4. Общая схема устройства струнного гравиметра

Этот принцип в абсолютных измерениях не используется из-за сложностей определения эффективной длины реальной струны.

Для относительных измерений используется схема, приведенная на рис. 1.4. Груз 1 подвешен на струне 2, проходящей между полюсами постоянного магнита 3, поэтому колебания струны приводят к возникновению в ней переменного тока. Чтобы ток не затухал, струна включена в контур с положительной обратной связью, образуя струнный генератор.

Частота струнного генератора умножается и сравнивается с частотой эталонного генератора. Для устранения продольных колебаний струны применяется электромагнитное демпфирование при помощи постоянных магнитов 4, возможность маятниковых колебаний ограничивают плоские горизонтальные пружины. Изменение напряженности поля Δg связано с изменением частоты колебаний струны Δ f квадратичной зависимостью:

, (1.20)

где , (1.21)

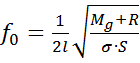, (1.22)

M - масса груза, l – длина струны, σ – плотность материала струны, S – площадь поперечного сечения струны, R – величина, зависящая от параметров вспомогательных пружин. Поскольку точное измерение величин, определяющих коэффициент С, является сложной задачей, здесь применяют способы градирование, которые используются в статических гравиметрах (см. ниже). Достоинства струнного гравиметра – практически неограниченный диапазон измерения и малая зависимость частоты колебаний струны от температуры, а также простота измерений и цифровой регистрации. Недостатки струнного гравиметра – слабая устойчивость к влиянию вибраций и других инерционных помех, а также нелинейная зависимость между Δg и f. Струнные гравиметры применяют для измерений в скважинах и иногда – на самолетах и морских судах.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: