 |
Расчет реакции электрической цепи методом переменных состояния
|
|
|
|
ВВЕДЕНИЕ
Курсовая работа по курсу «Основы радиоэлектроники» один из этапов самостоятельной работы, который позволяет определить и исследовать реакцию  (t) электрической цепи на несинусоидальное периодическое напряжение, а также закрепить знания по символическому методу и методу переменных состояния
(t) электрической цепи на несинусоидальное периодическое напряжение, а также закрепить знания по символическому методу и методу переменных состояния
РАСЧЕ РЕАКЦИИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ СИМВОЛИЧЕСКИМ МЕТОДОМ
Разложение заданного сигнала в ряд Фурье
Для разложения заданного сигнала, необходимо определить функцию, по которой происходит изменение сигнала, на промежутке равном периоду Т сигнала:
 если
если 
 если
если 
Разложим заданную функцию в ряд Фурье:

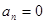

Так как заданный сигнал – нечетная функция, то 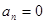 . Таким образом амплитуда комплексного напряжения для n-той гармоники описывается выражением:
. Таким образом амплитуда комплексного напряжения для n-той гармоники описывается выражением:

Нахождение Y -параметров активного четырехполюсника
Для активного четырехполюсника уравнения в Y-параметрах будет иметь вид:

Параметры  и
и  найдем из условия
найдем из условия  (короткое замыкание на выходе четырехполюсника)
(короткое замыкание на выходе четырехполюсника)

Рисунок 1.1 –Схема расчета параметров активного четырехполюсника при коротком замыкании выхода
В этом случае:
 (1.1)
(1.1)
 ;
;
 ; (1.3)
; (1.3)
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
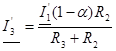 ;
;
 ;
;
 См (1.8)
См (1.8)
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 См
См
Параметры  и
и  найдем из условия
найдем из условия  (короткое замыкание на входе четырехполюсника).
(короткое замыкание на входе четырехполюсника).

Рисунок 1.2 – Схема расчета параметров активного четырехполюсника при коротком замыкании входа
В этом случае:
 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;

 ;
;
 См
См
 ;
;
 См
См
Нахождение Y -параметров пассивного четырехполюсника
Для пассивного четырехполюсника уравнения в Y-параметрах будут иметь вид:

Найдем параметры  и
и  при условии
при условии  (короткое замыкание выхода четырехполюсника).
(короткое замыкание выхода четырехполюсника).
|
|
|
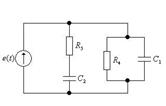
Рисунок 1.4 – Схема расчета параметров пассивного четырехполюсника при коротком замыкании выхода
В этом случае:
 ;
;  ;
;  ;
;
 См
См
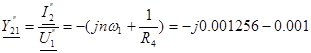 См
См
Найдем параметры  и
и  при условии
при условии  (короткое замыкание выхода четырехполюсника).
(короткое замыкание выхода четырехполюсника).

Рисунок 1.5 – Схема расчета параметров пассивного четырехполюсника при коротком замыкании входа
В этом случае:
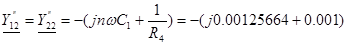 См
См
Нахождение Y -параметров сложного четырехполюсника
Матрица Y-параметров сложного четырехполюсника может быть найдена как сумма матриц Y-параметров активного и пассивного четырехполюсника. Таким образом, получаем:
 ;
;
 ;
;
 ;
;
 +
+  ;
;
Расчет коэффициента передачи
При параллельном соединении четырехполюсников коэффициент передачи можно определить по формуле:
 ,
,
где  .
.
Вычисления произведем с помощью программного продукта MathCAD 2000. результаты расчетов представлены в таблице 1.1
Расчет спектра отклика
Гармонические составляющие выходного напряжения определяются как  , результаты расчетов представим в таблице 1.1.
, результаты расчетов представим в таблице 1.1.
Таким образом реакция цепи описывается соотношением:

где  .
.
Временная функция отклика в виде 3-х гармоник имеет вид:
 (t)=119.55+95.64sin(1256.64t-0.8657)+13.22sin(3769.91t-1.23)+
(t)=119.55+95.64sin(1256.64t-0.8657)+13.22sin(3769.91t-1.23)+
+4.89sin(6283.18t-1.28)
Данные мгновенных значений напряжения  (t) для интервала времени от 0 до 5 мс представлены в таблице 1.2.
(t) для интервала времени от 0 до 5 мс представлены в таблице 1.2.
Таблица 1.1
| Гармоники | 1 | 2 | 3 | 4 | 5 |
 , мВ , мВ
| 6.366197 | 0 | 2.122065 | 0 | 1.273239 |
 , , 
| 1256.64 | 0 | 3769,91 | 0 | 6283.18 |
 , См , См
| 0.051618279+j0.00174387 | 0 | 0.0519404+j0.0040159302 | 0 | 0.0519815+j0.0064352979 |
 , См , См
| -0.00102499-j0.00125664 | 0 | -0.00102499-j0.00376992 | 0 | -0.00102499-j0.0062832 |
 , См , См
| -0.0048507184-j0.001256 | 0 | -0.0048507184-j0.003768 | 0 | -0.048507184-j0.00628 |
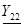 , См , См
| -0.0010287392-j0.00125664 | 0 | -0.0010287392-j0.00376992 | 0 | -0.0010287392-j0.0062832 |
 , Ом , Ом
| 387.72553-j487.23141 | 0 | 65.73629-j247.82057 | 0 | 24.70441-j155,22275 |

| 9.73558395-j11.4417114 | 0 | 2.08018708-j5.87373582 | 0 | 1.09439739-j3.68338887 |
 , мВ , мВ
| 61.9786453-j72.8401888 | 0 | 4.4142922-j12.4644492 | 0 | 1.3934294-j4.6898344 |
|
|
|
Таблица 1.2

|  , мВ , мВ
| 
|  , мВ , мВ
| 
|  , мВ , мВ
|
| 0 | 29.562 | 0.00175 | 200.62 | 0.0035 | 80.304 |
| 0.00025 | 67.078 | 0.002 | 210.566 | 0.00375 | 60.58 |
| 0.0005 | 109.798 | 0.00225 | 220.27 | 0.004 | 46.081 |
| 0.00075 | 138.707 | 0.0025 | 209.537 | 0.00425 | 38.48 |
| 0.001 | 158.795 | 0.00275 | 172.022 | 0.0045 | 28.534 |
| 0.00125 | 178.519 | 0.003 | 129.301 | 0.00475 | 18.831 |
| 0.0015 | 193.019 | 0.00325 | 100.393 | 0.005 | 29.563 |
График зависимости  (t), построенный в соответствии с таблицей 1.2, представлен на рис 1.3
(t), построенный в соответствии с таблицей 1.2, представлен на рис 1.3
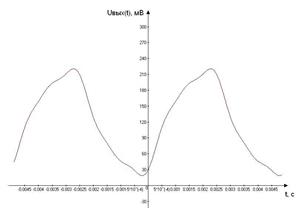
Рисунок 1.3 – Результат расчета реакции цепи на воздействие периодического негармонического сигнала
РАСЧЕТ РЕАКЦИИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ МЕТОДОМ ПЕРЕМЕННЫХ СОСТОЯНИЯ
Подлежащая расчету методом переменных состояния схема с выбранными положительными направлениями тока в ветвях приведена на рис.2.1

Рисунок 2.1-Схема для расчета реакции цепи на воздействие нескольких периодов входного сигнала методом переменных состояний
Формируем уравнения относительно переменных состояний  Запишем уравнения по законам Кирхгофа, которые содержат токи емкостей:
Запишем уравнения по законам Кирхгофа, которые содержат токи емкостей:

Так как  то:
то:
 (2.1)
(2.1)
По законам Кирхгофа, определим токи входящие в (2.1):
 (2.2)
(2.2)

Получаем:

Решая систему (2.2) получаем:

Получаем:

Для решения системы уравнений переменных состояния и нахождения отклика на заданное воздействие воспользуемся программным пакетом MathCAD2000 Professional.

Рисунок 2.2 – Реакция цепи (переходной процесс) на действие двух периодов заданного кусочно-непрерывного сигнала
Выводы
В ходе работы над курсовым проектом анализировалась схема линейной цепи. Были рассчитаны реакции  электрической цепи на несинусоидное периодическое напряжение, при параллельном соединении активного и пассивного четырехполюсник, двумя методами: а)- символичным методом, использую разложение данного сигнала в ряд Фурье, б)- методом переменных состояния (для двух периодов воздействия входного сигнала).
электрической цепи на несинусоидное периодическое напряжение, при параллельном соединении активного и пассивного четырехполюсник, двумя методами: а)- символичным методом, использую разложение данного сигнала в ряд Фурье, б)- методом переменных состояния (для двух периодов воздействия входного сигнала).
Полученные данные имеют некоторое отличие это связано с применением двух различных методов расчета. В целом полученные расхождения удовлетворяют погрешности расчетов.
СПИСОК ЛИТЕРАТУРЫ
1. Попов В.П.Основы теории цепей: Учеб для вузов. M.: Высш.шк., 1985.-490с.
2. 3ернов Н.В.,Карпов В.Г. Теория радиотехнических цепей-М. Энергия, 1972. -715с.
З. Афанасьев В.П. и др. Теория линейных электрических цепей:, Учебное пособие для вузов. -М.: Высш. шк., 1973.-592 с.
|
|
|
4. Белецкий А.Ф. Теория линейных электрических цепей: Учебн. для вузов. -М.: Радио и связь,1986.-544 с.
5. Коваль Ю.О. и др. Основы теории цепей: Учеб для вузов. M.: Харьков:ХНУРЭ; Колегиум, 2004.-436с.
6. Олександров Ю. М., Головенко В. М., Чурилов О. И. Методические указания к курсовой работе по дисциплине “Теория электрических и электронных цепей”. – Х. 2007-24с.
|
|
|


