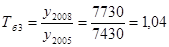 |
Расчет и анализ статистических показателей оплаты труда с использование пакета прикладных программ MS Excel
|
|
|
|
Содержание
Расчет среднегодовой заработной платы
Расчет средних значений интервалов
Расчет относительных величин
Расчет средних величин
Графическое определение моды
Графическое определение медианы
Расчет показателей вариации
Корреляционно-регрессивный анализ
Анализ рядов динамики
Расчет индексов
Расчет и анализ статистических показателей оплаты труда с использование пакета прикладных программ MS Excel
Для выполнения заданий расчетно-аналитической части в таблице 1 представлены исходные выборочные данные по организациям одной из отраслей хозяйствования в отчетном году (выборка 20 %-ная, бесповторная).
Таблица 1. Статистическая информация о результатах производственной деятельности организаций.
| № организации | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. |
| 1 | 162 | 11,340 |
| 2 | 156 | 8,112 |
| 3 | 179 | 15,036 |
| 4 | 194 | 19,012 |
| 5 | 165 | 13,035 |
| 6 | 158 | 8,532 |
| 7 | 220 | 26,400 |
| 8 | 190 | 17,100 |
| 9 | 163 | 12,062 |
| 10 | 159 | 9,540 |
| 11 | 167 | 13,694 |
| 12 | 205 | 21,320 |
| 13 | 187 | 16,082 |
| 14 | 161 | 10,465 |
| 15 | 120 | 4,32 |
| 16 | 162 | 11,502 |
| 17 | 188 | 16,356 |
| 18 | 164 | 12,792 |
| 19 | 192 | 17,471 |
| 20 | 130 | 5,85 |
| 21 | 159 | 9,858 |
| 22 | 162 | 11,826 |
| 23 | 193 | 18,142 |
| 24 | 158 | 8,848 |
| 25 | 168 | 13,944 |
| 26 | 208 | 23,920 |
| 27 | 166 | 13,280 |
| 28 | 207 | 22,356 |
| 29 | 161 | 10,948 |
| 30 | 186 | 15,810 |
Для начала рассчитаем среднегодовую заработную плату работников по формуле:
Для решения данной задачи воспользуемся пакетом MS Excel.
Полученные данные разместим в таблице 2.
Таблица 2. Среднегодовая заработная плата 1 работника, тыс. руб.
| № органи-зации | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. |
| 1 | 162 | 11,340 | 70,00 |
| 2 | 156 | 8,112 | 52,00 |
| 3 | 179 | 15,036 | 84,00 |
| 4 | 194 | 19,012 | 98,00 |
| 5 | 165 | 13,035 | 79,00 |
| 6 | 158 | 8,532 | 54,00 |
| 7 | 220 | 26,400 | 120,00 |
| 8 | 190 | 17,100 | 90,00 |
| 9 | 163 | 12,062 | 74,00 |
| 10 | 159 | 9,540 | 60,00 |
| 11 | 167 | 13,694 | 82,00 |
| 12 | 205 | 21,320 | 104,00 |
| 13 | 187 | 16,082 | 86,00 |
| 14 | 161 | 10,465 | 65,00 |
| 15 | 120 | 4,32 | 36,00 |
| 16 | 162 | 11,502 | 71,00 |
| 17 | 188 | 16,356 | 87,00 |
| 18 | 164 | 12,792 | 78,00 |
| 19 | 192 | 17,471 | 90,99 |
| 20 | 130 | 5,85 | 45,00 |
| 21 | 159 | 9,858 | 62,00 |
| 22 | 162 | 11,826 | 73,00 |
| 23 | 193 | 18,142 | 94,00 |
| 24 | 158 | 8,848 | 56,00 |
| 25 | 168 | 13,944 | 83,00 |
| 26 | 208 | 23,920 | 115,00 |
| 27 | 166 | 13,280 | 80,00 |
| 28 | 207 | 22,356 | 108,00 |
| 29 | 161 | 10,948 | 68,00 |
| 30 | 186 | 15,810 | 85,00 |
|
|
|
По данным таблицы 2 проведём аналитическую группировку совокупности включающей 30 предприятий.
Группировочным признаком является среднегодовая заработная плата.
Зададим количество групп 5.
Величину интервала определим по формуле:
ширина интервала h = 16,8.
Обозначим границы групп:
1-я группа – 36,0 – 52,8
2-я группа – 52,8 – 69,6
3-я группа – 69,6 – 86,4
4-я группа – 86,4 – 103,2
5-я группа – 103,2 – 120,0
Полученные интервальные ряды разместим в таблице 3.
Таблица 3. Интервальный ряд распределения предприятий по среднегодовой заработной плате.
| Группы предприятий по среднегодовой заработной плате, x | Число предприятий в группе, fi | Накопленная численность группы, S |
| 36-52,8 | 3 | 3 |
| 52,8-69,6 | 6 | 9 |
| 69,6-86,4 | 12 | 21 |
| 86,4-103,2 | 5 | 26 |
| 103,2-120,0 | 4 | 30 |
| Итого | 30 |
Отберем показатели характеризующие группы и определим их величины по каждой группе. Результаты группировки занесем в таблицу 4 и определим итоги по каждому показателю.
Таблица 4. Группировка предприятий по показателям характеризующим группы.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. |
| 36-52,8 | 3 | 406 | 18,28 | 133,00 |
| 52,8-69,6 | 6 | 956 | 58,19 | 365,00 |
| 69,6-86,4 | 12 | 2031 | 160,40 | 945,00 |
| 86,4-103,2 | 5 | 957 | 88,08 | 459,99 |
| 103,2-120,0 | 4 | 840 | 94,00 | 447,00 |
| Итого | 30 | 5190 | 418,95 | 2349,99 |
|
|
|
Таблица 5. Группировка предприятий по показателям характеризующим группы (в % к итогу.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. |
| 36-52,8 | 10 | 7,8 | 4,36 | 5,66 |
| 52,8-69,6 | 20 | 18,4 | 13,89 | 15,53 |
| 69,6-86,4 | 40 | 39,1 | 38,29 | 40,21 |
| 86,4-103,2 | 17 | 18,5 | 21,02 | 19,58 |
| 103,2-120,0 | 13 | 16,2 | 22,44 | 19,02 |
| Итого | 100 | 100 | 100 | 100 |
Из таблицы 5 видно, что в основном преобладают предприятия со среднегодовой заработной платой в интервале 69,6-86,4 40,0%, на долю которых приходится 39,29% всего фонда заработной платы.
Полученные данные для наглядности можно представить в виде диаграммы рисунок 1. Для решения данной задачи воспользуемся пакетом прикладных программ MS Excel.
Рис 1. Диаграмма распределения предприятий по среднегодовой заработной плате.
При помощи графического метода построим графики полученного ряда распределения.
Для построения полигона и гистограммы необходимо определить срединное значение интервала по формуле:
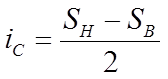
Где: SН — нижняя граница интервала;
SВ — верхняя граница интервала.
Полученные данные разместим в таблице 6.
Таблица 6. Определение срединного значения интервала
| Группы предприятий по среднегодовой заработной плате | Срединное значение интервала, тыс. руб. | Число предприятий в группе |
| 36-52,8 | 44,4 | 3 |
| 52,8-69,6 | 61,2 | 6 |
| 69,6-86,4 | 78,0 | 12 |
| 86,4-103,2 | 94,8 | 5 |
| 103,2-120,0 | 111,6 | 4 |
| Итого | 30 |
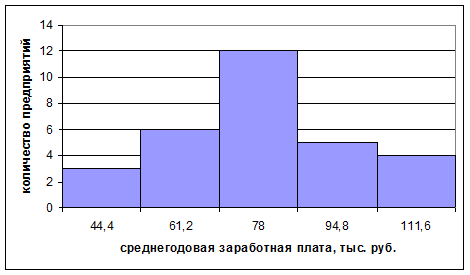
Рис.2. Гистограмма распределения предприятий по среднегодовой заработной плате.
Рис. 3. Полигон распределения предприятий по среднегодовой заработной плате.
Рассчитаем относительный показатель структуры(ОПС) по формуле:
Полученные данные разместим в таблице 7.
Таблица 7. Расчет относительных показателей структуры в % к итогу.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. | ||
| в % к итогу | ||||||
| 36-52,8 | 10 | 7,8 | 4,36 | 5,66 | ||
| 52,8-69,6 | 20 | 18,4 | 13,89 | 15,53 | ||
| 69,6-86,4 | 40 | 39,1 | 38,29 | 40,21 | ||
| 86,4-103,2 | 17 | 18,5 | 21,02 | 19,58 | ||
| 103,2-120,0
| 13 | 16,2 | 22,44 | 19,02 | ||
| Итого | 100 | 100 | 100 | 100 | ||
Рассчитаем относительный показатель координации (ОПК) по формуле:
Полученные данные разместим в таблице 8.
Таблица 8. Расчет относительных показателей координации в % к базе.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. |
| 69,6-86,4 | 12 | 2031 | 160,40 | 945,00 |
| в % к базе. | ||||
| 36-52,8 | 25 | 20 | 11 | 14 |
| 52,8-69,6 | 50 | 46 | 36 | 38 |
| 86,4-103,2 | 41 | 47 | 54 | 48 |
| 103,2-120,0 | 33 | 41 | 58 | 47 |
Рассчитаем относительный показатель интенсивности (ОПИ) по формуле:
Полученные данные разместим в таблице 9.
Таблица 9. Расчет относительных показателей интенсивности.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Относительный показатель интенсивности, тыс. руб. |
| 36-52,8 | 3 | 406 | 18,28 | 45,02 |
| 52,8-69,6 | 6 | 956 | 58,19 | 60,86 |
| 69,6-86,4 | 12 | 2031 | 160,40 | 78,97 |
| 86,4-103,2 | 5 | 957 | 88,08 | 92,03 |
| 103,2-120,0 | 4 | 840 | 94,00 | 11,19 |
| Итого | 30 | 5190 | 418,95 | - |
Рассчитаем относительный показатель сравнения (ОПС) по формуле:
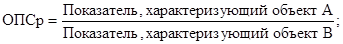
Полученные данные разместим в таблице 10.
Таблица 10. Расчет относительных показателей сравнения.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. |
| 69,6-86,4 | 12 | 2031 | 160,40 | 945,00 |
| во сколько раз меньше базовой. | ||||
| 36-52,8 | 4 | 5 | 8,7 | 7,1 |
| 52,8-69,6 | 2 | 2,1 | 2,7 | 2,5 |
| 86,4-103,2 | 2,4 | 2,1 | 1,8 | 2,0 |
| 103,2-120,0 | 3 | 2,4 | 1,7 | 2,1 |
Рассчитаем среднюю арифметическую простую по формуле:
Полученные данные разместим в таблице 11.
Таблица 11. Расчет средней арифметической.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. | ||
| 36-52,8
| 3 | 135,33 | 6,09 | 44,33 | ||
| 52,8-69,6 | 6 | 159,33 | 9,70 | 60,83 | ||
| 69,6-86,4 | 12 | 169,25 | 13,37 | 78,75 | ||
| 86,4-103,2 | 5 | 191,40 | 17,62 | 92,00 | ||
| 103,2-120,0 | 4 | 210,00 | 23,50 | 111,75 |
Рассчитаем среднюю арифметическую взвешенную по формуле:
где х i – вариант, а mi – частота или статистический вес.
Полученные данные разместим в таблице 12.
Таблица 12. Расчет средней арифметической взвешенной.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Среднесписочная численность работников, чел. | Фонд заработной платы, млн. руб. | Среднегодовая заработная плата 1 работника, тыс. руб. |
| Итого | 30 | 173,00 | 13,97 | 78,33 |
Рассчитаем среднюю гармоническую взвешенную по формуле:
Полученные данные разместим в таблице 13.
Таблица 13. Расчет средней гармонической взвешенной.
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Фонд заработной платы, млн. руб. V | Среднегодовая заработная плата 1 работника X, руб. | V / x Руб. | V V / x Руб. |
| 36-52,8 | 3 | 18280000 | 133000 | 137,44 | - |
| 52,8-69,6 | 6 | 58190000 | 365000 | 159,42 | - |
| 69,6-86,4 | 12 | 160400000 | 945000 | 169,74 | - |
| 86,4-103,2 | 5 | 88080000 | 459990 | 191,48 | - |
| 103,2-120,0 | 4 | 94000000 | 447000 | 210,29 | - |
| Итого | - | 418950000 | - | 868,38 | 482451,8 |
Рассчитаем моду по формуле:
где х о – начальная нижняя граница модального интервала;
h – величина интервала;
f 2 – частота модального интервала;
f 1 – частота интервала, предшествующая модальному;
f 3 – частота интервала следующая за модальным.
Данные для расчета в таблице 3.
Найдем моду:
Делаем вывод: по моде – наиболее часто встречается заработная плата в размере 74,6 тыс. руб.,
Рассчитаем медиану по формуле:
где хо – нижняя граница медианного интервала;
Σf/2 – порядковый номер медианы (N);
S Me -1 – накопленная частота до медианного интервала;
fMe – частота медианного интервала.
Данные для расчета в таблице 3.
найдем N медианы: N = Σfi/2 = 30/2 = 15.
По накопленным частотам определим, что пятнадцатая единица находится в интервале (69,6 - 86,4), ее значение определим по формуле:
Делаем вывод по медиане – половина работников получает среднегодовую заработную плату ниже 78 тыс. руб., а половина – выше.
Определим моду графическим способом по гистограмме (рис. 1).
В прямоугольнике, имеющем наибольшую высоту, проводим две линии, как показано на рис.4, и из точки их пересечения опускаем перпендикуляр на ось абсцисс. Значение х на оси абсцисс в этой точке есть мода (Мо). Согласно рис. 4 Мо» 78 тыс. руб. То есть в большинстве предприятий среднегодовая заработная составляет более 78 тыс. руб.
Для графического определения медианы необходимо построить кумуляту по накопленным частотам. Так как мы пользовались инструментом «Гистограмма», то кумулята уже построена (рис. 5). Из точки на оси ординат, соответствующей половине всех частот, проводим прямую, параллельную оси абсцисс, до пересечения ее с кумулятурой. Опустив из этой точки перпендикуляр на ось абсцисс, находим значение медианы (Ме).
|
|
|
 |
Рис.4. Кумулята (графическое определение медианы)
По рис. 5 Ме»78 тыс. руб. То есть половина исследуемых предприятия выплачивает среднегодовую заработную плату около 78 тыс. руб.
Рассчитаем среднюю заработную плату по формуле средней арифметической взвешенной, так как даны частоты усредняемой величины:
.
Таблица 14. Данные для расчета показателей вариации
| Группы предприятий по среднегодовой заработной плате | Число предприятий в группе | Расчетные показатели | |||
| fi | xi (ср. значение интервала) | хifi | (хi –  )
| (хi – )2fi
| |
| 36-52,8 | 3 | 44,4 | 133,2 | -34,2 | 3500,7 |
| 52,8-69,6 | 6 | 61,2 | 367,2 | -17,4 | 1808,2 |
| 69,6-86,4 | 12 | 78,0 | 936 | -0,6 | 3,8 |
| 86,4-103,2 | 5 | 94,8 | 474 | 16,2 | 1318,7 |
| 103,2-120,0 | 4 | 111,6 | 446,4 | 33,0 | 4366,6 |
| Итого | 30 | х | 2356,8 | -2,8 | 10998,0 |
Тогда средняя заработная плата составляет:
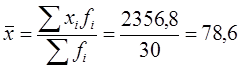
тыс. руб.
Определим размах вариации:
тыс. руб.
Определим дисперсию на основании данных таблицы 14.
тыс. руб.
Определим среднее квадратическое отклонение по формуле:
тыс. руб.
Определим коэффициент вариации:
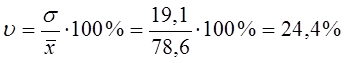
Таким образом, колеблемость средней заработной платы по группам предприятий от своего среднего значения составляет 24,4 %, следовательно, совокупность устойчива (так как ниже верхней границы в 25 %) и средняя величина является типичной и характерной для всей совокупности.
Вычислим среднюю арифметическую по исходным данным. Так как здесь не даны частоты изучаемого явления, то средний валовой доход определим как среднюю арифметическую простую. Для этого используем функцию пакета Excel. В результате расчетов (см. ячейку D35 лист 1 MS Excel. приложение 1) получили значение 78,3 тыс. руб. Эта средняя не намного отличается от средней, полученной ранее (всего на 0,3 тыс. руб.), так как здесь не учитывается число предприятий и определяется просто срединное значение в ряду.
Рассчитаем парную регрессию по формуле:
Необходимые для решения суммы рассчитаны в таблице 15. Подставим их в уравнение и решим систему.
Таблица 15. Расчет показателей для нахождения уравнения регрессии.
| № п/п | Число предприятий в группе xi, | Фонд заработной платы, млн. руб. yi, | x2 | y2 | xy | 
|
| 1 | 3 | 18,28 | 9 | 334,15 | 54,84 | 45,89 |
| 2 | 6 | 58,19 | 36 | 3386,07 | 349,14 | 83,78 |
| 3 | 12 | 160,40 | 144 | 25728,16 | 1924,80 | 159,56 |
| 4 | 5 | 88,08 | 25 | 7758,08 | 440,40 | 71,15 |
| 5 | 4 | 94,00 | 16 | 8836,00 | 376,00 | 58,52 |
| ∑* | 30 | 418,95 | 230 | 175519,10 | 3144,78 | 418,9 |
Из системы уравнений получим a1 = 12,63; а0 = 8.
Получив искомое уравнение регрессии 
можно утверждать, что с увеличение количества предприятий, увеличивается фонд заработной платы.
*Если параметры уравнения найдены верно, то ∑y=∑yх.
Рассчитаем линейный коэффициент корреляции по формуле:
Найдем коэффициент корреляции по данным табл. 15.
Найденный коэффициент корреляции 0 < r = 0,109 < 1; означает, что характер связи между исследуемыми признаками прямой.
По степени тесноты, связи между признаками практически отсутствуют 0 ≤ r ≤ ±0,3.
Рассчитаем смыкание рядов динамики по данным таблицы 16.
Таблица 16. Данные для расчета смыкания рядов динамики.
| Годы | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| Оборот торговли магазина, тыс. руб. (в фактически действующих ценах) | 41,78 | 42,12 | 43,66 | |||
| Оборот торговли магазина, тыс. руб. (в сопоставимых ценах) | 52,40 | 52,60 | 53,40 | 54,10 | ||
| Сомкнутый ряд абсолютных величин (в сопоставимых ценах; тыс. руб.) | 50,13 | 50,54 | 52,40 | 52,60 | 53,40 | 54,10 |
Чтобы проанализировать динамику общего объема торговли магазина за 2003-2008 гг., необходимо сомкнуть (объединить) приведенные выше два ряда в один. А чтобы уровни нового ряда были сопоставимы, необходимо пересчитать данные 2003-2008 гг. в сопоставимые цены. Для этого на основе данных об объеме торговли за 2005 г. в фактических и сопоставимых ценах находим соотношение между ними: 52,40: 43,66 = 1,2. Умножая на полученный коэффициент данные за 2003-2005 гг., приводим их, таким образом, к сопоставимому виду с последующими уровнями. Сомкнутый (сопоставимый) ряд динамики показан в последней строке таблицы 16.
Произведем расчет и анализ динамики дорожно-транспорных происшествий в районе за 2005–2008 гг., по данным табл. 17.
За базу сравнения примем уровень 2005 года.
Таблица 17. Показатели дорожно-транспортных происшествий за 2005-2008гг.
| Показатели | Год | ||||
| 2005 | 2006 | 2007 | 2008 | ||
| Дорожно-транспортные происшествия | 7430 | 7650 | 7680 | 7730 | |
| Абсолютные приросты, ∆y | |||||
| Цепные | Базисные | ||||
| ∆yц1 = y2006−y2005 =7650-7430=220 | ∆yб1 = y2006−y2005 =7650-7430=220 | ||||
| ∆yц2 = y2007−y2006 =7680-7650=30 | ∆yб2 = y2007−y2005 =7680-7430=250 | ||||
| ∆yц3 = y2008−y2007 =7730-7680=50 | ∆yб3 = y2008−y2005 =7730-7430=300 | ||||
| Темпы роста, Тр | |||||
| Цепные | Базисные | ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
| Темпы прироста, Тпр | |||||
| Цепные | Базисные | ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
В таблице 18 приведем всю совокупность показателей ряда динамики, позволяющую посмотреть взаимосвязи между ними.
Таблица 18. Показатели изменения уровней ряда динамики
| Показатели | Год | |||
| 2005 | 2006 | 2007 | 2008 | |
| Дорожно-транспортные происшествия | 7430 | 7650 | 7680 | 7730 |
| 2. Темпы роста базисные: | − | 1,02 | 1,03 | 1,04 |
| 2.1. коэффициенты | ||||
| 2.2. проценты | − | 102 | 103 | 104 |
| 3. Темпы роста цепные: | − | 1,02 | 1,001 | 1,001 |
| 3.1. коэффициенты | ||||
| 3.2. проценты | − | 102 | 100,1 | 100,1 |
| 4. Абсолютные приросты, ед. | − | 220 | 250 | 300 |
| 4.1. базисные (2005 г.) | ||||
| 4.2. цепные (по годам) | − | 220 | 30 | 50 |
| 5. Темпы прироста базисные | − | 0,02 | 0,03 | 0,04 |
| 5.1. коэффициенты | ||||
| 5.2. проценты | − | 2 | 3 | 4 |
| 6. Темпы прироста цепные | − | 0,02 | 0,001 | 0,001 |
| 6.1. коэффициенты | ||||
| 6.2. проценты | − | 2 | 0,1 | 0,1 |
| 7. Абсолютное значение 1 %пр. | − | 110 | 300 | 500 |
Рассчитаем средние показатели в рядах динамики по данным таблицы 19
Таблица 19. Динамика изменения соотношения количества автомобилей и жителей г. (количество автомобилей на 1000 жителей на начало года).
| Моменты времени (год) | 1993 | 1998 | 2003 | 2006 | 2008 |
| Уровни ряда (количество автомобилей на 1000 жителей на начало года). | 480 | 525 | 630 | 698 | 756 |
Таблица 20 Расчетные показатели для определения среднего уровня ряда динамики
| Периоды времени | Количество автомобилей xi | Продолжительность периода, лет ti | у i ·ti |
| 1993-1997 | 480 | 5 | 2400 |
| 1998-2002 | 525 | 5 | 2625 |
| 2003-2005 | 630 | 3 | 1890 |
| 2006-2007 | 698 | 2 | 1396 |
| 2008 | 756 | 1 | 756 |
| Итого | 16 | 9067 |
рассчитаем средний уровень ряда динамики, представленного в таблице 20:
Это означает, что средне количество автомобилей на 1000 жителей за 1993–2008 гг. − 566,7 штук.
Произведем расчет индивидуальных индексов.
Таблица 21. Данные об отчислениях в фонд социального страхования компании «---------------------» за пять лет.
| Годы | 1998 | 1999 | 2000 | 2001 | 2002 |
| Отчисления в ФСС, тыс.руб. | 192,54 | 231,97 | 265,07 | 282,53 | 311,28 |
Исчислим цепные индексы отчислений в ФСС с 1998 к 2002 году, в %:
=106,06%;
=102,85%;
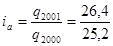=104,76%;
=101,51%.
В результате расчетов получили индивидуальные цепные индексы отчислений в фонд социального страхования компании «-----------------------» за пять лет с 1998 по 2002 годы. Данные представим в таблице 22.
Таблица 22. Цепные индексы отчислений в ФСС компании «--------------------» за пять лет.
| Годы | 1998 | 1999 | 2000 | 2001 | 2002 |
| Отчисления в ФСС, тыс.руб. | - | 1,0606 | 1,0285 | 1,0476 | 1,0151 |
рассчитаем базисные индексы, в %. За базу примем значение 1998 года.
=106,06%;
=110,82%;
=114,28%;
=116,01%.
В результате расчетов получили индивидуальные базисные индексы отчислений в фонд социального страхования компании «-------------».
Оформим их в таблицу 23.
Таблица 23. Базисные индексы отчислений в ФСС компании «-------------------------».
| Годы | 1998 | 1999 | 2000 | 2001 | 2002 |
| Отчисления в ФСС, тыс.руб. | - | 1,0606 | 1,1082 | 1,1428 | 1,1601 |
Произведем расчет общих индексов.
Таблица 24. Данные о работе автозаправочной станции.
| Наименование нефтепродуктов | Ед. изм.,тыс. литров | Базисный | Отчетный | ||
Цена за ед.изм.,  ,
тыс.руб.
| Кол-во
| Цена заед. изм.  ,
тыс. руб.
| Кол-во 
| ||
| А | 15 | 3 | 15,5 | 5 | |
| Б | 45 | 2 | 44 | 3 | |
| В | 8 | 7 | 9 | 8 | |
Рассчитаем агрегатный индекс цен в зависимости от выбранных соизмерителей 
:
=2,150 или 215,0 %.
По данному ассортименту товаров цены повысились в среднем на 115 %. по сравнению с базисным периодом.
=1060-493=567 тыс. руб.
Полученная величина прироста говорит о том, что повышение цен на данный ассортимент товара в среднем на 115 %. Обусловило увеличение объема товарооборота в текущем периоде на 567 тыс.руб.
Рассчитаем соизмеритель – количества реализации продукции в базисном, 
.
=1,886 или 188,6 %
По ассортименту в целом повышение цены составило в среднем 88,6 %
Определим величину прироста товарооборота:
=366-194=172 тыс.руб.
Полученная величина прироста показывает, что повышение цен в среднем на 88,6%, обусловливает увеличение объема товарооборота на 172 тыс. руб.
Произведем расчет средних индексов.
Таблица 25. Данные для расчета средних индексов.
| Наименование нефтепродуктов | Стоимость продукции в базисном году, тыс.руб., 
| Индексы физического
объема продукции
в отчетном году, 
|
| А Б В | 45 90 56 | 6,500 1,120 2,833 |
| Итого: | 191 |
Для данного расчета используем формулу:
=2,8897=288,97%
Физический объем продукции по трем наименованиям увеличился на 188,97%.
|
|
|
