 |
Методы изучения комбинаторных объектов и чисел
|
|
|
|
1. Теоретико-множественный подход.
Примером использования такого подхода является принцип включений и исключений. Согласно нему, число 
объектов, не удовлетворяющих ни одному из свойств набора 
, определяется равенством
N 0 = N – 
+ 
+ … +
+ (– 1) k 
+ … + (–1) n N (1, 2, …, n). (1)
Число 
объектов, удовлетворяющих точно k свойствам из набора , равно
Nk = 
+ …+(– 1) s – k 
+
+…+ (–1) n – k 
× N (1, 2, …, n). (2)
Задача 1. В отделе НИИ каждый сотрудник владеет хотя бы одним иностранным языком. Известно, что английским языком владеют 6 человек, немецким – 6, французским – 7, английским и немецким – 4, немецким и французским – 3, английским и французским – 2, все три языка знает 1 человек. Определить, сколько всего человек в отделе, сколько человек владеют только английским, только немецким, только французским, и сколько человек знает только 1 иностранный язык.
Решение. Согласно условиям задачи N 0 = 0, т.к. в отделе нет сотрудников, не владеющих иностранными языками. Следовательно, по формуле (1) получаем:
N = 
– 
+ N (1, 2, 3) (3)
N = (6 + 6 + 7) – (4 + 3 + 2) + 1 = 11 человек всего в отделе.
Для вычисления остальных показателей также воспользуемся формулой (1). Найдем, например N(только А) – число человек, не владеющих никаким другим языком, кроме английского. Для этого формулу (1) надо применить только к множеству людей, владеющих английским языком. В этом случае n = 2. Тогда N = N (A), N (1) и N (2) – число людей, владеющих, помимо английского, еще немецким и французским, соответственно, N (1, 2) – число людей, владеющих помимо английского еще одновременно немецким и французским. Отсюда
N (только A) = 6 – (4 + 2) + 1 = 1.
Аналогично
N (только Н) = 6 – (4 + 3) + 1 = 0.
N (только Ф) = 7 – (2 + 3) + 1 = 3.
Вычислим теперь N 1 – число людей, владеющих только 1 языком. Воспользуемся формулой (2) при k = 1.
|
|
|
N 1 = N (1) + N (2) + N (3) + (–1)2–1× 
× [ N (1,2) + N (2,3) + N (1,3)] +
+ (–1)3–1× 
× N (1,2,3) = 6 + 6 + 7 – 2×(4 + 3 + 2) + 3×1 = 4.
Такой же результат получим, если сложим N (только A) + N (только Н) + N (только Ф).
2. Алгебраические методы.
Приведем основные свойства числа сочетаний.
1) 
= 
2) = 
+ 
3) 
4) 
– бином Ньютона.
5) 
6) 
3. Метод производящих функций.
Последовательности { un }, фигурирующей в какой-либо задаче, например, комбинаторной, удобно поставить в соответствие формальный степенной ряд
,
который называется производящей функцией данной последовательности.
Задача 2.Найти производящую функцию, формулу общего члена последовательности и 
, зная рекуррентное соотношение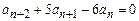 
и начальные члены 
, 
.
Решение.Найдем производящую функцию последовательности 
.
Коэффициенты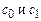 
определим как коэффициенты произведения производящих функций из соотношений:
, 
.
Следовательно, 
.
Формулу общего члена последовательности можно получить, разложив производящую функцию на простые дроби и приведя подобные при одинаковых степенях. Однако проще воспользоваться теоремой об общем виде решения линейного рекуррентного соотношения. Выпишем характеристический многочлен соотношения 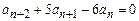и найдём его корни.
Уравнение 
, согласно теореме Виета имеет два простых корня 
, т.е. 
. Тогда общее решение линейного рекуррентного соотношения имеет вид
.
Коэффициенты 
определяются из начальных условий, т.е. из системы линейных уравнений 
. Решив данную систему, получим 
. Следовательно, 
, а 
.
Контрольные вопросы и задания
1. Определить наибольший коэффициент разложения 
, если сумма всех его коэффициентов равна 4096.
2. Найти наибольший член разложения 
.
3. Найти коэффициент при 
в разложении
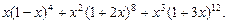
4. Определить число членов разложения 
.
5. Найти коэффициент при в разложении 
.
6. Найти коэффициент при 
в разложении 
.
7. Найти коэффициент при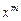 
в разложении
|
|
|
.
8. Найти коэффициент при 
и 
в разложении 
.
9. В каком из выражений 
или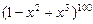 
будет наибольший коэффициент при .
10. Доказать, что: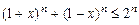 
.
11. Вычислить суммы:
a) 
;
b) 
;
c) 
;
d) 
;
e) 
;
f) 
;
g) 
;
h) 
;
i) 
;
j) 
;
k) 
l) 
.
12. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38, с ветчиной – 42, и с сыром и с колбасой – 28, и с колбасой и с ветчиной – 31, и с сыром и с ветчиной – 26. Все 3 вида бутербродов взяли 25 человек, а несколько человек захватили с собой пирожки. Сколько человек взяли с собой пирожки? Только бутерброды с ветчиной? Только два вида бутербродов?
13. Сколькими способами можно посадить за круглый стол 7 мужчин и 7 женщин так, чтобы никакие две женщины не сидели рядом?
14. Девушка написала 5 писем и подписала 5 конвертов. Спеша на свидание, она разложила письма по конвертам, не сверив имя адресата с адресом. Сколько имеется вариантов, когда ни одно письмо не дойдёт до своего адресата?
15. Найти общее решение рекуррентного соотношения:
a) 
;
b) 
;
c)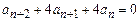 
;
d) 
;
e) 
;
f) 
;
g) 
;
h) 
.
16. Найти производящую функции, формулу общего члена последовательности и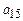 
, зная рекуррентное соотношение и начальные члены:
a) 
, 
, 
;
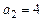b) 
, 
, 
;
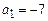c) 
, 
, 
, 
;
d) 
, 
, 
.
17. Найти производящую функцию и общее решение рекуррентного соотношения: 
, 
, 
, найти 
.
18. Доказать, что члены последовательности Фибоначчи 
удовлетворяют следующим соотношениям:
a) 
;
b) 
;
c)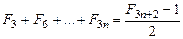 
;
d)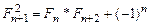 
;
e) 
.
Библиографический список
Основной
1. Новиков, Ф.А. Дискретная математика для программистов [Текст]: учебное пособие для студ. вузов (гриф МО) / Ф. А. Новиков. - 2-е изд. - СПб.: ПИТЕР, 2006. - 364 с.
2. Забуга, А.А. Теоретические основы информатики: учеб. пособие / А.А. Забуга – Новосибирск: Изд-во НГТУ, 2013. – 168 с. (http://www.iprbookshop.ru)
3. Губарев, В.В. Введение в теоретическую информатику: учеб. пособие / В.В. Губарев – Новосибирск: Изд-во НГТУ, 2015. – Ч. 2. – 472 с. ( http://www.knigafund.ru )
Дополнительный
4. Комбинаторный анализ. Задачи и упражнения [Текст]: учебное пособие / Под ред. Рыбникова Н.А. - М.: Наука,1985. - 210 с.
5. Липский, В. Комбинаторика для программистов [Текст] / В. Липский - М.: Мир, 1988. - 213 с.
Электронное издание
МНОЖЕСТВА. ЭЛЕМЕНТЫ
КОМБИНАТОРНОГО АНАЛИЗА
Методические указания
к практическим занятиям
|
|
|
Для студентов, обучающихся по направлениям
09.03.02 – “Информационные системы и технологии”
09.03.03 – “Прикладная информатика”
очной формы обучения
Составители БУГАЕВ Юрий Владимирович,
ШУРУПОВА Ирина Юрьевна,
ЛИТВИНОВ Дмитрий Анатольевич
Подписано в печать..201. Формат 60х84 1/16
Усл. печ. л.. Тираж 50 экз. Заказ С-
ФГБОУ ВПО “Воронежский государственный университет инженерных технологий”
(ФГБОУ ВПО “ВГУИТ”)
Отдел полиграфии ФГБОУ ВПО “ВГУИТ”
Адрес академии и отдела полиграфии:
394036, Воронеж, пр. Революции, 19
|
|
|
