 |
Необходимые определения и обозначения
|
|
|
|
Содержание
Перечень условных обозначений
Введение
1. Необходимые определения и обозначения
2. Используемые результаты
3. Определения, примеры и общие свойства  -перестановочных подгрупп
-перестановочных подгрупп
4. Конечные группы с заданными  -перестановочными подгруппами
-перестановочными подгруппами
Заключение
Список использованных источников
Перечень условных обозначений
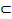 – знак строгого включения множеств;
– знак строгого включения множеств;
 – знак включения множеств;
– знак включения множеств;
 – принадлежность элемента множеству;
– принадлежность элемента множеству;
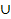 – объединение множеств;
– объединение множеств;
 – пересечение множеств;
– пересечение множеств;
 –
–  является подгруппой группы
является подгруппой группы  ;
;
 –
–  является собственной подгруппой группы
является собственной подгруппой группы  ;
;
 –
–  является максимальной подгруппой группы
является максимальной подгруппой группы  ;
;
 –
–  является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
 –
–  является субнормальной подгруппой группы
является субнормальной подгруппой группы  ;
;
 –
–  является минимальной нормальной подгруппой группы
является минимальной нормальной подгруппой группы  ;
;
Скобки  применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
 – подгруппа, сопряжённая подгрупп
– подгруппа, сопряжённая подгрупп  посредством элемента
посредством элемента  ;
;
 – циклическая группа порядка
– циклическая группа порядка  ;
;
 – симметрическая группа степени
– симметрическая группа степени  ;
;
 – ядро подгруппы
– ядро подгруппы  в группе
в группе  , т.е. пересечение всех подгрупп, сопряжённых с
, т.е. пересечение всех подгрупп, сопряжённых с  в
в  ;
;
 – подгруппа, порожденная всеми подгруппами, сопряженными с подгруппой
– подгруппа, порожденная всеми подгруппами, сопряженными с подгруппой  из
из  элементами
элементами  из
из  , то есть
, то есть  ;
;
 – централизатор множества T в группе G;
– централизатор множества T в группе G;
 – центр группы G;
– центр группы G;
 – нормализатор подгруппы
– нормализатор подгруппы  в группе
в группе  ;
;
 – наибольшая нормальная подгруппа нечетного порядка группы
– наибольшая нормальная подгруппа нечетного порядка группы  ;
;
 – наибольшая нормальная
– наибольшая нормальная  –подгруппа группы
–подгруппа группы  ;
;
 –
–  –холловская подгруппа группы
–холловская подгруппа группы  ;
;
 – силовская
– силовская  –подгруппа группы
–подгруппа группы  ;
;
 – дополнение к силовской
– дополнение к силовской  –подгруппе в группе
–подгруппе в группе  , т.е.
, т.е. 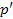 –холловская подгруппа группы
–холловская подгруппа группы  ;
;
 – группа G изоморфна группе
– группа G изоморфна группе  ;
;
|
|
|
Пусть  – группа,
– группа,  и
и  , тогда:
, тогда:
 – правый смежный класс,
– правый смежный класс,
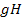 – левый смежный класс;
– левый смежный класс;
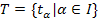 – правая трансверсаль подгруппы
– правая трансверсаль подгруппы 
в группе  ;
;
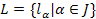 – левая трансверсаль подгруппы
– левая трансверсаль подгруппы 
в группе  ;
;
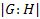 – индекс подгруппы
– индекс подгруппы  в группе
в группе  ;
;
 – порядок группы G;
– порядок группы G;
Пусть  и
и  – подгруппы группы
– подгруппы группы  и
и  , тогда:
, тогда:
 – двойной смежный класс группы
– двойной смежный класс группы  по подгруппам
по подгруппам
 и
и  ;
;
 – факторгруппа группы
– факторгруппа группы  по подгруппе
по подгруппе  ;
;
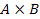 – прямое произведение подгрупп A и B;
– прямое произведение подгрупп A и B;
 – цоколь группы
– цоколь группы  ;
;
 – коммутатор элементов
– коммутатор элементов 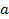 и
и  ;
;
 – коммутант группы G;
– коммутант группы G;
 – множество всех простых чисел;
– множество всех простых чисел;
 – дополнение к
– дополнение к  во множестве
во множестве  , где
, где  – некоторое множество простых чисел;
– некоторое множество простых чисел;
 –
–  -длина группы
-длина группы  .
.
Введение
Напомним, что подгруппа  группы
группы  перестановочна с подгруппой
перестановочна с подгруппой  , если
, если  . Если
. Если  перестановочна со всеми подгруппами группы
перестановочна со всеми подгруппами группы  , то она называется перестановочной [6] или квазинормальной в
, то она называется перестановочной [6] или квазинормальной в  [7].
[7].
Так как для двух перестановочных подгрупп  и
и  произведение
произведение  также является подгруппой в
также является подгруппой в  , то понятие перестановочных подгрупп является одним из наиболее важных обобщений понятия нормальных подгрупп.
, то понятие перестановочных подгрупп является одним из наиболее важных обобщений понятия нормальных подгрупп.
Перестановочные подгруппы имеют много интересных свойств. Как известно, например, что каждая перестановочная подгруппа является восходящей [8] и, если она является перестановочной подгруппой в некоторой конечной порождённой группе  , то
, то  субнормальна в
субнормальна в  [8].
[8].
Но фактически эти два результата были получены как обобщения следующего наблюдения: каждая перестановочная подгруппа конечной группы является субнормальной [7].
Разрабатывая этот результат Ito и Szep доказали, что для каждой перестановочной подгруппы  конечной группы
конечной группы  ,
,  – нильпотентна [9].
– нильпотентна [9].
Немного позже было доказано, что при таких условиях,  [18].
[18].
При некоторых естественных условиях мы встречаемся с ситуацией, когда некоторые подгруппы  и
и  группы
группы  неперестановочны, но существует подгруппа
неперестановочны, но существует подгруппа  такая, что
такая, что 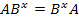 для некоторого
для некоторого 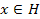 .
.
Основываясь на этом наблюдении мы дадим следующие определения.
|
|
|
Определение 1 Пусть  ,
,  – подгруппы группы
– подгруппы группы  и
и  . Тогда мы говорим, что:
. Тогда мы говорим, что:
(1)  является
является  -перестановочной с
-перестановочной с  , если для некоторого
, если для некоторого  имеем
имеем  .
.
(2)  является наследственно
является наследственно  -перестановочной с
-перестановочной с  , если
, если  для некоторого
для некоторого  .
.
Заметим, что  – перестановочные подгруппы также являются перестановочными подгруппами. Во втором приведённом случае мы имеем дело с
– перестановочные подгруппы также являются перестановочными подгруппами. Во втором приведённом случае мы имеем дело с  -перестановочными подгруппами, которые были исследованы и использованы в [].
-перестановочными подгруппами, которые были исследованы и использованы в [].
Определение 2 Подгруппа  группы
группы  называется (наследственно)
называется (наследственно)  -перестановочной, если она (наследственно) перестановочна со всеми подгруппами группы
-перестановочной, если она (наследственно) перестановочна со всеми подгруппами группы  .
.
Целью данной работы является изложение некоторых известных разделов теории перестановочных подгрупп, изучение и применение некоторых свойств  -перестановочных подгрупп.
-перестановочных подгрупп.
Необходимые определения и обозначения
Бинарной алгебраической операцией на множестве 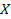 называют отображение декартова квадрата
называют отображение декартова квадрата  во множество
во множество 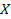 . Если
. Если  – бинарная операция на
– бинарная операция на 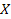 , то каждой упорядоченной паре
, то каждой упорядоченной паре  элементов из
элементов из 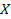 соответствует однозначно определенный элемент
соответствует однозначно определенный элемент  . Бинарную операцию на
. Бинарную операцию на 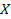 обозначают одним из символов:
обозначают одним из символов:  и т.д. Если, например, вместо
и т.д. Если, например, вместо  условимся писать
условимся писать 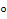 , то вместо
, то вместо  пишем
пишем  .
.
Говорят, что на множестве X определена бинарная операция (умножение), если 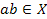 для всех
для всех  .
.
Если  для всех
для всех  , то операция называется ассоциативной.
, то операция называется ассоциативной.
Если  для всех
для всех  , то операция называется коммутативной.
, то операция называется коммутативной.
Элемент  называется единичным, если
называется единичным, если  для всех
для всех 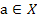 .
.
Обратным к элементу  называется такой элемент
называется такой элемент  , что
, что  .
.
Полугруппой называется непустое множество  с бинарной алгебраической операцией (умножение), удовлетворяющей следующим требованиям:
с бинарной алгебраической операцией (умножение), удовлетворяющей следующим требованиям:
(1) операция определена на  , т.е.
, т.е. 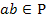 для всех
для всех  и
и  ;
;
(2) операция ассоциативна, т.е.  для любых
для любых  .
.
Группой называется непустое множество  с бинарной алгебраической операцией (умножением), удовлетворяющей следующим требованиям:
с бинарной алгебраической операцией (умножением), удовлетворяющей следующим требованиям:
(1) операция определена на  , т.е.
, т.е.  для всех
для всех  и
и 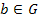 ;
;
(2) операция ассоциативна, т.е.  для любых
для любых  ;
;
(3) в  существует единичный элемент, т.е. такой элемент
существует единичный элемент, т.е. такой элемент  , что
, что  для всех
для всех 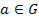 ;
;
(4) каждый элемент обладает обратным, т.е. для любого 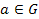 существует такой элемент
существует такой элемент  , что
, что 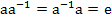 .
.
Группу с коммутативной операцией называют коммутативной или абелевой.
|
|
|
Если G – конечное множество, являющееся группой, то G называют конечной группой, а число  элементов в
элементов в  – порядком группы
– порядком группы  .
.
Также группой называется непустое множество  с бинарной алгебраической операцией (умножением), удовлетворяющей следующим требованиям:
с бинарной алгебраической операцией (умножением), удовлетворяющей следующим требованиям:
(1) операция определена на  ;
;
(2) операция ассоциативна;
(3) уравнения  ,
,  имеют решения для любых элементов
имеют решения для любых элементов  .
.
Подмножество  группы
группы  называется подгруппой, если
называется подгруппой, если  – группа относительно той же операции, которая определена на группе
– группа относительно той же операции, которая определена на группе  . Для подгруппы используется следующее обозначение:
. Для подгруппы используется следующее обозначение:  . Запись
. Запись  читается так:
читается так:  – подгруппа группы
– подгруппа группы  .
.
Также можно дать следующее определение подгруппы конечной группы. Непустое подмножество  конечной группы
конечной группы  называется подгруппой, если
называется подгруппой, если  для всех
для всех 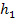 и
и 
Каждая группа  обладает единичной подгруппой
обладает единичной подгруппой  . Сама группа
. Сама группа  также считается подгруппой в
также считается подгруппой в  . Эти подгруппы называют тривиальными подгруппами. Нетривиальная подгруппа группы
. Эти подгруппы называют тривиальными подгруппами. Нетривиальная подгруппа группы  это такая подгруппа
это такая подгруппа  из
из  , которая отлична от
, которая отлична от  и отлична от единичной подгруппы
и отлична от единичной подгруппы  .
.
Собственной называется подгруппа, отличная от группы.
Пусть  – подмножество группы
– подмножество группы  и
и  . Через
. Через

обозначим подмножество всех элементов группы  вида
вида  , где
, где 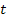 пробегает все элементы множества
пробегает все элементы множества  . Подмножество
. Подмножество  называется подмножеством, сопряженным подмножеству
называется подмножеством, сопряженным подмножеству  посредством элемента
посредством элемента  .
.
Подгруппа  называется подгруппой, сопряженной подгруппе
называется подгруппой, сопряженной подгруппе  посредством элемента
посредством элемента  .
.
Пусть  – непустое подмножество группы
– непустое подмножество группы  . Совокупность всех элементов группы
. Совокупность всех элементов группы  , перестановочных с каждым элементом множества
, перестановочных с каждым элементом множества  , называется централизатором множества
, называется централизатором множества  в группе
в группе  и обозначается через
и обозначается через  . Таким образом,
. Таким образом,

Центром группы  называется совокупность всех элементов группы
называется совокупность всех элементов группы  , перестановочных с каждым элементом группы
, перестановочных с каждым элементом группы  . Центр группы
. Центр группы  обозначается через
обозначается через  . Ясно, что
. Ясно, что  , т.е. центр группы
, т.е. центр группы  совпадает с централизатором подмножества
совпадает с централизатором подмножества  в группе
в группе  . Кроме того,
. Кроме того,
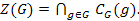
Зафиксируем элемент  в группе
в группе  . Пересечение всех подгрупп группы
. Пересечение всех подгрупп группы  , содержащих элемент
, содержащих элемент  , назовем циклической подгруппой, порожденной элементом
, назовем циклической подгруппой, порожденной элементом  , и обозначим через
, и обозначим через 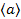 . Таким образом,
. Таким образом,
|
|
|

Для элемента  имеются следующие две возможности.
имеются следующие две возможности.
Все степени элемента  различны, т.е.
различны, т.е.  для целых
для целых  . В этом случае говорят, что элемент
. В этом случае говорят, что элемент  имеет бесконечный порядок.
имеет бесконечный порядок.
Имеются совпадения  при
при 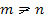 . Если, например,
. Если, например,  , то
, то 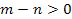 и
и  , т.е. существуют натуральные степени элемента
, т.е. существуют натуральные степени элемента  , равные единичному элементу. Наименьшее натуральное число
, равные единичному элементу. Наименьшее натуральное число  , при котором
, при котором  называют порядком элемента
называют порядком элемента  и пишут
и пишут 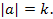
Если группа  совпадает с одной из своих циклических подгрупп, то группу
совпадает с одной из своих циклических подгрупп, то группу  называют циклической группой. В этом случае в группе
называют циклической группой. В этом случае в группе  имеется элемент
имеется элемент  такой, что
такой, что  , все элементы в группе
, все элементы в группе  являются целыми степенями элемента
являются целыми степенями элемента  :
:
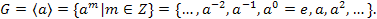
Если элемент  имеет бесконечный порядок, то все эти элементы в группе
имеет бесконечный порядок, то все эти элементы в группе  попарно различны и
попарно различны и  – бесконечная циклическая группа.
– бесконечная циклическая группа.
Если элемент  имеет конечный порядок
имеет конечный порядок  , то
, то  , т.е. циклическая группа
, т.е. циклическая группа  , порожденная элементом
, порожденная элементом  порядка
порядка  , состоит из
, состоит из  элементов. В этом случае
элементов. В этом случае  – конечная циклическая группа порядка
– конечная циклическая группа порядка  .
.
Две группы  и
и  называются изоморфными, если существует биекция
называются изоморфными, если существует биекция  такая, что
такая, что  для всех
для всех  . Факт изоморфизма записывают так:
. Факт изоморфизма записывают так:  .
.
Пусть  – группа,
– группа,  и
и  . Правым смежным классом группы
. Правым смежным классом группы  по подгруппе
по подгруппе  называется множество
называется множество

всех элементов группы  вида
вида  , где
, где  пробегает все элементы подгруппы
пробегает все элементы подгруппы  .
.
Аналогично определяется левый смежный класс

Пусть  – подгруппа группы
– подгруппа группы  . Подмножество
. Подмножество 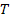 элементов группы
элементов группы  называется правой трансверсалью подгруппы
называется правой трансверсалью подгруппы  в группе
в группе  , если
, если 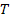 содержит точно один элемент из каждого правого смежного класса группы
содержит точно один элемент из каждого правого смежного класса группы  по подгруппе
по подгруппе  . Итак, если
. Итак, если

– правая трансверсаль подгруппы  в группе
в группе  , то
, то

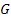 – конечная группа, то число различных правых смежных классов по подгруппе
– конечная группа, то число различных правых смежных классов по подгруппе  также будет конечно, оно называется индексом подгруппы
также будет конечно, оно называется индексом подгруппы  в группе
в группе 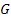 и обозначается через
и обозначается через  . Ясно, что индекс подгруппы
. Ясно, что индекс подгруппы  в конечной группе
в конечной группе  совпадает с числом элементов в правой трансверсали
совпадает с числом элементов в правой трансверсали  подгруппы
подгруппы  , т.е.
, т.е.
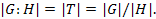
Аналогично определяется левая трансверсаль подгруппы  в группе
в группе  . Если
. Если

– левая трансверсаль подгруппы  в группе
в группе 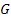 , то
, то

Ясно, что индекс подгруппы  в конечной группе
в конечной группе  совпадает с числом элементов в левой трансверсали
совпадает с числом элементов в левой трансверсали  подгруппы
подгруппы  , т.е.
, т.е.  .
.
Пусть  и
и 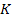 – подгруппы группы
– подгруппы группы  и
и  . Множество
. Множество

называется двойным смежным классом группы  по подгруппам
по подгруппам  и
и  .
.
При  двойной смежный класс
двойной смежный класс

превращается в произведение подгрупп  и
и 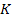 . В общем случае
. В общем случае  не является подгруппой.
не является подгруппой.
Говорят, что подгруппы  и
и 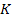 перестановочны, если
перестановочны, если  . Равенство
. Равенство  означает, что для любых
означает, что для любых 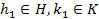 существуют
существуют  такие, что
такие, что  .
.
Если  , то говорят, что группа
, то говорят, что группа  есть произведение своих подгрупп
есть произведение своих подгрупп  и
и  , либо группа
, либо группа  факторизуема подгруппами
факторизуема подгруппами  и
и  . В этом случае каждый элемент
. В этом случае каждый элемент  представим в виде
представим в виде  , где
, где  .
.
|
|
|
Подгруппа  называется нормальной подгруппой группы
называется нормальной подгруппой группы  , если
, если  для всех
для всех  .
.
Запись  читается так:
читается так:  – нормальная подгруппа группы
– нормальная подгруппа группы  Равенство
Равенство 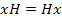 означает, что для любого элемента
означает, что для любого элемента  существует элемент
существует элемент  такой, что
такой, что  .
.
В каждой группе  тривиальные подгруппы (единичная подгруппа
тривиальные подгруппы (единичная подгруппа  и сама группа
и сама группа  ) являются нормальными подгруппами. Если в неединичной группе
) являются нормальными подгруппами. Если в неединичной группе  нет других нормальных подгрупп, то группа
нет других нормальных подгрупп, то группа  называется простой. Единичную группу
называется простой. Единичную группу  считают непростой группой.
считают непростой группой.
Пусть  – нормальная подгруппа группы
– нормальная подгруппа группы  . Обозначим через
. Обозначим через  совокупность всех левых смежных классов группы
совокупность всех левых смежных классов группы  по подгруппе
по подгруппе  , т.е.
, т.е.
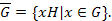
Группа  называется факторгруппой группы
называется факторгруппой группы  по подгруппе
по подгруппе  и обозначается через
и обозначается через  .
.
Пусть  – простое число. p-группой называют конечную группу, порядок которой есть простого степень числа
– простое число. p-группой называют конечную группу, порядок которой есть простого степень числа  . Ясно, что подгруппы и факторгруппы любой
. Ясно, что подгруппы и факторгруппы любой  -группы также являются
-группы также являются  -группами. Конечная группа называется примарной, если она является
-группами. Конечная группа называется примарной, если она является  -группой для некоторого простого
-группой для некоторого простого  .
.
Силовской p-подгруппой конечной группы  называют такую
называют такую  -подгруппу, индекс которой не делится на
-подгруппу, индекс которой не делится на  .
.
Каждая нормальная подгруппа  группы
группы  определяет цепочку
определяет цепочку  . Обобщая эту ситуацию, цепочку
. Обобщая эту ситуацию, цепочку

вложенных друг в друга нормальных подгрупп группы  называют нормальным рядом в
называют нормальным рядом в  .
.
Ряд называется субнормальным, если выполняется более слабое условие: каждый предыдущий его член есть нормальная подгруппа следующего члена, т.е.  для
для 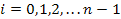
Члены субнормальных рядов называются субнормальными подгруппами (если подгруппа  субнормальна в
субнормальна в 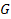 , то пишут (
, то пишут ( ).
).
Ясно, что каждый нормальный ряд является субнормальным.
Пусть 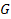 – группа,
– группа,  и
и  – ее подгруппы. Напомним, что произведение
– ее подгруппы. Напомним, что произведение  определяется как множество элементов
определяется как множество элементов  , где
, где 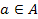 ,
, 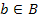 . Если
. Если 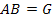 , то говорят, что группа
, то говорят, что группа 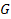 является произведением своих подгрупп
является произведением своих подгрупп  и
и  . В этом случае каждый элемент
. В этом случае каждый элемент  представим в виде
представим в виде  , где
, где 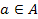 ,
, 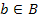 .
.
Произведение  называется прямым, если подгруппы
называется прямым, если подгруппы  и
и  нормальны в
нормальны в 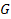 и
и  . Прямое произведение обозначают так:
. Прямое произведение обозначают так:  . Итак, группа
. Итак, группа 
|
|
|


