 |
Описание и обоснование выбора метода решения
|
|
|
|
ВВЕДЕНИЕ
В данный момент существует много программ для решения уравнений, вычисления интегралов и дифференциалов: MathCAD, MATLAB, и т.д. Они имеют высокую точность вычисления, высокую функциональность, но имеют и свои недостатки. Главные из них – сложный непонятный интерфейс, высокая многофункциональность недоступна рядовому пользователю.
Рынок нуждается в более простых аналогах приведенных выше программ. Созданный программный продукт способен решать уравнения с одной переменной методом Ньютона (касательных). Он прост в эксплуатации, имеет интуитивно понятный интерфейс и способен выстраивать график уравнения, что является очень важным для пользователя.
Программа будет полезна всем, как студентам высших учебных заведений, так и школьникам.
ПОСТАНОВКА ЗАДАЧИ
Цель создания программного продукта
Главной целью работы является разработка программы способной решать уравнения с одной переменной методом Ньютона (касательных), что должно являться пособием для студентов высших учебных заведений и для учащихся математических классов среднеобразовательных школ в снижении ненужной нагрузки, связанной с многочисленными массивами вычислений.
Постановка задачи
В данном программном продукте необходимо реализовать решение двух видов уравнений: y(x) =a×ln(b×x), y(x) =ax2+bx+c. Вместо коэффициентов должны использоваться параметры a, b, c, которые принимают значения, вводимые пользователем. Для нахождения корней, обязательным является указание промежутков, на которых определена функция, поэтому пользователь обязательно вводит промежутки функции m, n. Метод Ньютона является итерационным методом, следовательно, должна указываться погрешность вычисления ε. Обязательным является построение графика выбранной функции на заданном промежутке.
|
|
|
МАТЕМЕТИЧЕСКАЯ МОДЕЛЬ
Дисциплина "Численные методы" содержит набор методов и алгоритмов приближенного (численного) решения разнообразных математических задач, для которых точное аналитическое решение либо не существует, либо слишком сложно для использования на практике. При численном решении задач всегда возникает погрешность.
Выделяют абсолютную и относительную погрешность. Пусть р – точное значение искомого ответа, а p – приближённое значение, полученное с помощью численного метода.
Тогда 
– абсолютная погрешность,
– относительная погрешность.
На первом этапе необходимо найти отрезок [a,b], на котором функция имеет ровно один корень. На втором этапе происходит уточнение корня на отрезке с заданной точностью с помощью одного из численных методов.
Метод, реализуемый в РУОП, называется методом Ньютона. Другое название метода – метод касательных.
Начальное условие:
Дано:
уравнение f(x) =0,
где f(x) ÎC'' [m,n], f(m) ×f(n) <0,
f'(x) и f''(x) знакопостоянны на отрезке [m,n];
точность e.
Найти: решение уравнения с заданной точностью.
Пусть корень 
где 
– некоторое приближение к корню,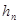 
– необходимая поправка. Разложим f(x) линейно в ряд Тейлора в окрестности xn (что соответствует замене функции в точке на касательную):
f(ξ) =0=f(xi+hi) ≈f(xi) +f'(xi) ×hi.
Отсюда:
.
Закон получения приближений к корню:
(2.1)
Начальное приближение x0 выбирается из условия:
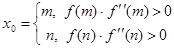. (2.2)
 |
Графическая иллюстрация метода приведена на рисунке 2.1. Начальная точка в этом случае совпадает с n.
Рисунок 2.1. – Метод Ньютона
Идея метода заключается в том, что последовательность приближений к корню строится путем проведения касательных к графику функции и нахождения их точек пересечения с осью ОХ.
|
|
|
Алгоритм метода.
Шаг 1. Найти первое приближение к корню x0 по формуле (2.2).
Шаг 2. Находить следующие приближения к корню по формуле (2.1), пока не выполнится условия окончания:
|xi-xi+1|<e.
Последнее найденное приближение и будет корнем.
ОПИСАНИЕ И ОБОСНОВАНИЕ ВЫБОРА МЕТОДА РЕШЕНИЯ
Для обоснования выбора метода Ньютона для нахождения корней уравнений с одной переменной рассмотрим два другие итерационные метода.
Метод половинного деления
Другое название метода – метод дихотомии.
Дано:
уравнение f(x) =0,
где f(x) ÎC [m,n], f(m) ×f(n) <0;
точность e.
Найти: решение уравнения с заданной точностью.
Другими словами, необходимо найти нуль функции на отрезке с заданной точностью. При этом функция непрерывна и в концах отрезка принимает значения разных знаков.
Алгоритм метода:
 |
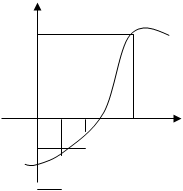Шаг 1. Отрезок делится пополам. Находится точка с: = (b+a) /2 (см. рисунок 3.1).
f(x)
f(n)
0mkn
x
f(m)
Рисунок 3.1. – Метод половинного деления
Шаг 2. Проверяются следующие условия.
1. Если f(c) =0 – корень найден.
2. Если f(a) ×f(c) <0 – корень на [a,c], поэтому b: =c.
3. Если f(c) ×f(b) <0 – корень на [c,b], поэтому a: =c.
Шаг 3. Проверяется условие |a-b|<ε. Если условие выполнено, то считается, что корень найден. В этом случае он принимается равным а (хотя можно принять его равным b или даже (a+b) /2). Иначе переход к шагу 1.
Метод итераций
Дано:
уравнение f(x) =0,
где f(x) ÎC' [m,n], f(m) ×f(n) <0,
f'(x) знакопостоянна на отрезке [a,b];
точность e.
Найти: решение уравнения с заданной точностью.
Идея метода заключается в том, что от уравнения f(x) =0 переходим с помощью равносильных преобразований к уравнению вида x=φ(x).Т. е. задача сводится к нахождению абсциссы ξ точки пересечения двух графиков функции (см. рис.2). В общем случае φ(x) =x-f(x) *C.
 |
Рисунок 3.2. – Корень уравнения
Точка ξ, для которой выполняется ξ= φ(ξ), называется неподвижной точкой процесса итераций. Очевидно, что эта точка является корнем уравнения f(x) =0.
Константа С подбирается таким образом, чтобы функция φ(x) удовлетворяла условиям сходимости метода итераций:
1) 
– является непрерывной и дифференцируемой на [m,n];
2) значения 
;
|
|
|
3) 
для 
.
Если 
, то С нужно выбирать так, чтобы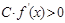 
и 
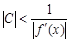для .
Метод состоит в построении последовательности приближений к корню. В качестве начального приближения выбирается любая точка x0Î [a,b]. Для определенности можно брать середину отрезка [a,b]. В качестве формулы получения последующих приближений выступает сама φ(x): 
Алгоритм метода:
Шаг 1. Найти первое приближение к корню x0 как середину отрезка [m,n].
Шаг 2. Находить следующие приближения к корню по формуле, пока не выполнится условия окончания:
|xi - xi+1|<e.
Последнее найденное приближение и будет корнем.
3.3. Обоснование выбора метода
При рассмотрении обоих методов видно, что скорость сходимости метода Ньютона (касательных) выше скорости сходимости метода секущих (хорд) и метода итераций, следовательно, оптимальным для реализации в программе является метод Ньютона.
|
|
|
