 |
Ответ: Суммы нет, ряд расходится.
|
|
|
|
Теорема «О двух милиционерах»
Если 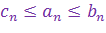 , то
, то 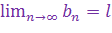 ,
, 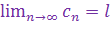
Следовательно, предел  существует и
существует и 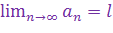
В качестве: 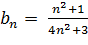
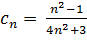
Следовательно: 
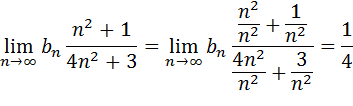
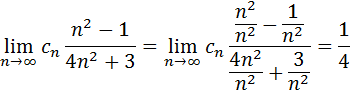
Ответ: 
Задача 3. Вычислить предел 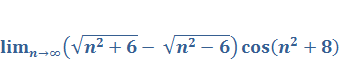
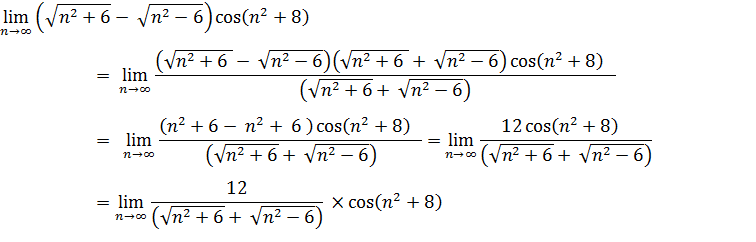
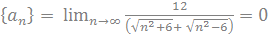 – бесконечно малая последовательность
– бесконечно малая последовательность
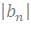 =
= 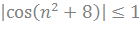 - последовательность ограничена
- последовательность ограничена
Следовательно,  бесконечно малая последовательность, т.к. произведение бесконечно малой последовательно на ограниченную есть бесконечно малая последовательность.
бесконечно малая последовательность, т.к. произведение бесконечно малой последовательно на ограниченную есть бесконечно малая последовательность.
Значит, 
Ответ: 0
Задача 4. Найдите, используя «первый замечательный предел» 

Ответ: 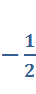
Задача 5. Найти 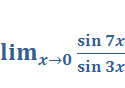 , используя «первый замечательный предел».
, используя «первый замечательный предел».
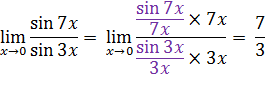
Ответ: 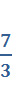
Задача 6. Найдите 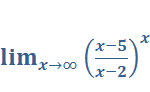 , используя «второй замечательный предел».
, используя «второй замечательный предел».
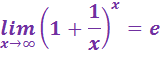
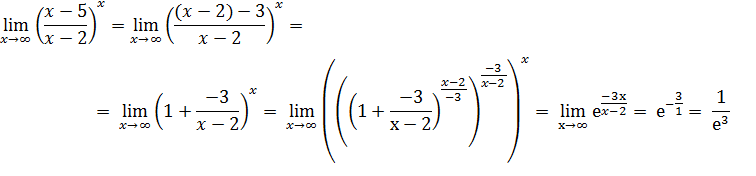
Ответ: 
Задача 7. Вычислить односторонние пределы 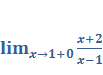

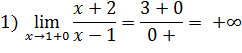
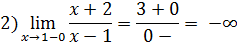
Ответ: 
Раздел 2. Дифференциальное исчисление функций одного аргумента
Задача 1. Вычислите производную  сложной функции
сложной функции 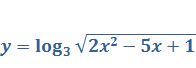
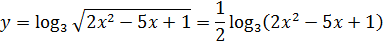
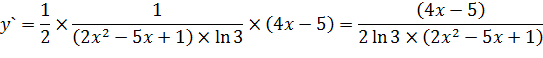
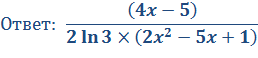
Задача 2. Используя логарифмическое дифференцирование, вычислите производную функции 
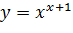
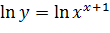
по свойству логарифмов 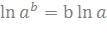
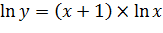
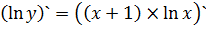

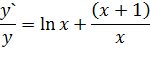

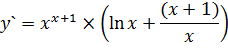
Ответ: 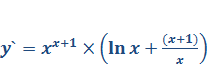
Задача 3. Используя дифференциал, вычислите приближенное значение 

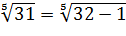
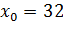
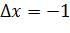
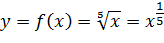

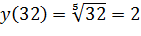

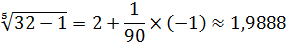

Задача 4. Найти производную от неявно заданной функции 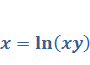
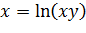


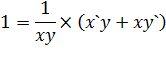


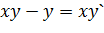
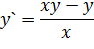

Раздел 3. Интегральное исчисление функций одного аргумента
Задача 6. Найдите определенный интеграл методом замены переменной.

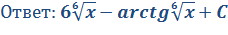
 Задача 9. Выполнив предварительно чертеж, найти площадь плоской фигуры, ограниченной графиками функций
Задача 9. Выполнив предварительно чертеж, найти площадь плоской фигуры, ограниченной графиками функций 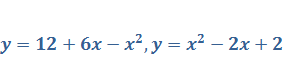
1. Найдем точки пересечения


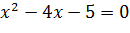
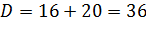
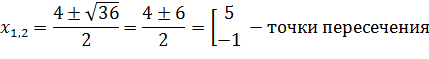
2. Найдем площадь
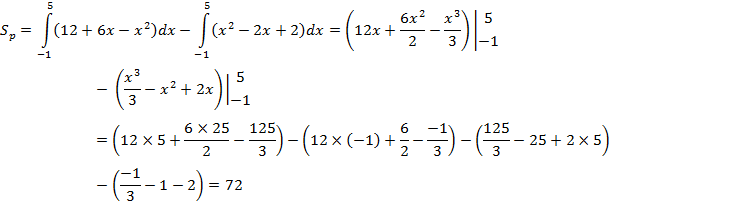
Ответ: 72
Раздел 4. Дифференциальное исчисление функций двух аргументов
Задача 1. Найди предел 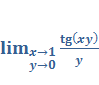
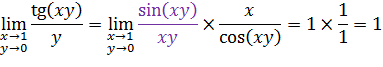
Ответ: 1
Задача 2. Найти частные производные  функции
функции 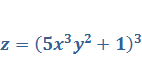
|
|
|
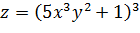
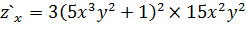
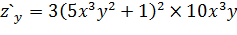
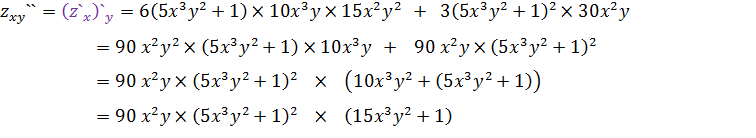
Задача 3. Найти частные производные  функции
функции 
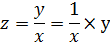
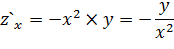
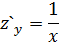

Задача 4. Найти условный экстремум функции  при наличии уравнения связи
при наличии уравнения связи 
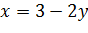

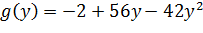

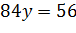
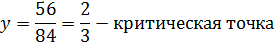
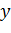
| 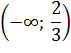
| 
| 
|
| + | - | |

| max |





Раздел 5. Числовые и функциональные ряды.
Задача 1. Пользуясь достаточным признаком расходимости, доказать расходимость ряда 
Решение:
Ряд называется сходящимся, если у него есть сумма.
Суммы у ряда 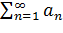 нет, если
нет, если 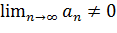
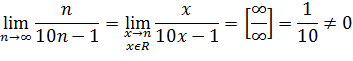
Ответ: Суммы нет, ряд расходится.
Задача 2. Найти радиус сходимости ряда 
Когда есть сумма, у неё есть область сходимости.
R – радиус сходимости
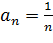 ;
; 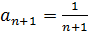
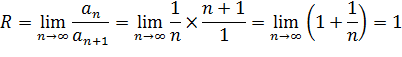
Ответ: R=1
Задача 3. Разложить в ряд Маклорена функцию 
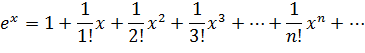
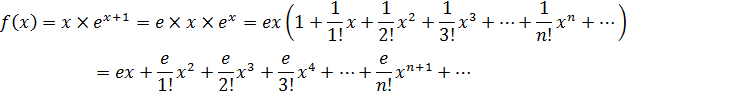
«Текстовые задачи» экзамена по математике
1. Предположим, что вами в муниципалитете получено разрешение на строительство капитального гаража. Согласно утвержденной документации имеются следующие ограничения: гараж должен иметь форму прямоугольного параллелепипеда, периметр основания которого не должен превышать 15 (м), а две его стены должны быть квадратной формы. Найдите такие длину и ширину гаража, чтобы объем внутреннего помещения был максимальным, в чем вы, как хозяин гаража, заинтересованы.
P=15 метров
V=x2y  max
max
| x |
| x |
| y |
P=2(x+y)=15 – уравнение связи
Y=-x+15/2
f’(x)=2x(15/2-x)-x2= -3x2+15x= -3x(x-5)
-3x(x-5)=0
x=0
x=5
y=2,5
Ответ: 5м, 5м, 2,5м
2. Стоянка автотранспорта имеет форму прямоугольника со сторонами 80  и 60
и 60  . По требованию муниципалитета вокруг стоянки было построено новое ограждение и проведено асфальтирование, в результате чего большая сторона стоянки уменьшилась на 1,2
. По требованию муниципалитета вокруг стоянки было построено новое ограждение и проведено асфальтирование, в результате чего большая сторона стоянки уменьшилась на 1,2 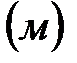 , а ее меньшая на 1,3
, а ее меньшая на 1,3  . Оценить приближенно с помощью дифференциала: на сколько уменьшилась площадь автостоянки. Проверьте эти расчеты на калькуляторе и оцените погрешность при вычислениях.
. Оценить приближенно с помощью дифференциала: на сколько уменьшилась площадь автостоянки. Проверьте эти расчеты на калькуляторе и оцените погрешность при вычислениях.
x0=80 ∆x= -1,2
y0=60 ∆y= -1,3
z=xy
Формула Эйлера
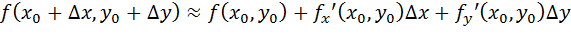

Ответ: 4624 м2
3. Для того чтобы оплатить услуги иностранной фирмы муниципалитету пришлось провести две банковские операции. В первый день перевели на счет фирмы 19 000 долларов по цене 35 рублей за 1 доллар, а на следующий день 19 989 долларов, но за счет падения курса доллара уже по цене 34 рубля 98 копеек за 1 доллар. Оцените приближенно с помощью дифференциала: как изменилась сумма расходов во второй день. Проверьте эти расчеты на калькуляторе и оцените погрешность при вычислениях.
|
|
|
1. 19000$
35руб. = 1$
2. 19989$
34,98руб. = 1$
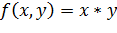
∆x=989$
∆y=-0.02руб.

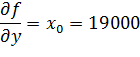
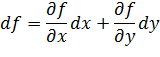
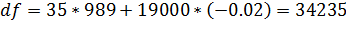
Ответ: 34 235
4. Кооператив открывает линию по производству жестяных консервных банок объемом 0,25 литра для последующей расфасовки в них консервированного горошка. Для кооператива экономически выгодно, чтобы вы рассчитали такие радиус основания x и высоту y консервной банки, чтобы на ее изготовление потребовалось минимум материала. Напомним, что 1 л = 1000 см 3.
V=250см3
V=πR2y=πx2y
πx2y=250

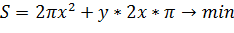
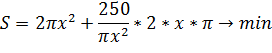
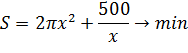

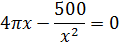
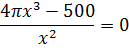
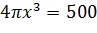
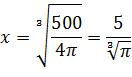
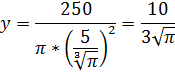
Ответ: 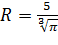

5. Муниципалитет готовит заказ на изготовление баков для сбора мусора для последующего размещения их во дворах жилых домов. Как руководителю ЖКХ вам надо рассчитать размеры бака (высоты h, длины x и ширины y основания) такими, чтобы на изготовление бака пошло бы минимум материала, и тем самым сэкономить деньги муниципалитету. Предполагается, что баки имеют объем V = 32 м 3, обладают формой прямоугольного параллелепипеда и не имеют крышек.
| h |
| x |
| y |
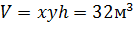

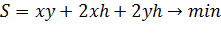
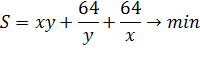

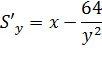

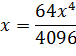
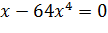
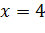
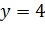
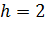
Ответ: 4м, 4м, 2м.
Задачи повышенной сложности
Задача 1. Найти значение а, при котором функция 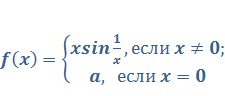 является непрерывной в точке
является непрерывной в точке 
Функция 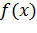 непрерывна в точке
непрерывна в точке 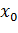 , если
, если 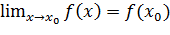
Для заданной в задаче функции:

Поскольку 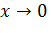 и и 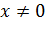
| 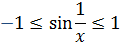
|
Таким образом, получаем произведение бесконечно малой  функции на ограниченную функцию функции на ограниченную функцию 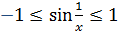
|
Ответ: 
Задача 2

Решение: Если 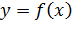 непрерывна и монотонна на [a,b], и
непрерывна и монотонна на [a,b], и  и
и  - разных знаков, то сущность
- разных знаков, то сущность 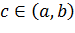 , что
, что 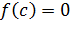
Проверим значение функции 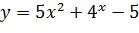 в точках
в точках
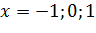
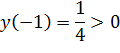
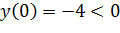
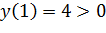
Непрерывна и монотонна на 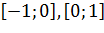 при этом на концах этих отрезков имеет разные знаки, следовательно, существуют точки
при этом на концах этих отрезков имеет разные знаки, следовательно, существуют точки  и
и 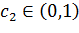
Ответ: Да, имеет.
Задача 3.

Получаем произведение бесконечно малой функции на ограниченную функцию 
|
|
|
|


