 |
Проверка гипотезы по критерию согласия Пирсона
|
|
|
|
По критерию Пирсона сравниваются теоретическая и эмпирическая функции плотности распределения вероятности, а точнее – частота попадания случайной величины в интервал. Интервалы могут быть любыми, равными и неравными, но удобно использовать те интервалы, на которых построена гистограмма. Эмпирические числа попадания n (из гистограммы) сравнивается с теоретическим npj, где pj – вероятность попадания случайной величины X в j -ый интервал:
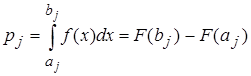, (20)
aj и bj – границы j -го интервала. Карл Пирсон показал, что, если все npj ³ 5, то суммарная квадратическая относительная разность между теоретическим и практическим числом попаданий в интервал равна
(21)
имеет приближенно c2 распределение Пирсона с k – m степенями свободы, где m – число параметров, оцениваемых по выборке, плюс 1. Так как параметров два, то m = 3. Выражение (21) представляет собой статистику Пирсона.
Теоретическое распределение можно считать подобранным верно, если выполняется условие
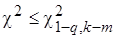. (22)
Построим таблицу результатов, в которую занесем: номера интервалов (1-й столбец), границы интервалов aj и bj (2-й и 3-й столбцы), вероятность попадания в интервал pj (4-й столбец), теоретическое число попаданий и практическое число попаданий npj (6-й столбец). Границы интервалов и практическое число попаданий взяты из гистограммы, теоретическая вероятность попадания в j-й интервал подсчитывается по выражению (20).
Практическая часть.
clear Tabl% очистили таблицу результатов
Tabl(:, 1)=[1:k]';% номера интервалов
Tabl(:, 2)=xm'-delta/2;% левые границы интервалов
Tabl(:, 3)=xm'+delta/2;% правые границы интервалов
Tabl (1,2)=-inf;% теоретическое начало 1-го интервала
Tabl (k, 3)=inf;% теоретический конец последнего интервала
|
|
|
Tabl(:, 4)=nj';% опытные числа попаданий
bor=[Tabl(:, 2); Tabl (end, 3)];% все границы интервалов
pro=cdf (tdistr{bdistr}, bor, param (bdistr, 1), param (bdistr, 2));
Tabl(:, 5)=pro (2:end) – pro (1:end-1);% вероятности попаданиz pj
Tabl(:, 6)=n*Tabl(:, 5);% теоретическое число попаданий npj
disp ('Сводная таблица результатов')
fprintf (' j aj bj')
fprintf (' nj pj npj\n')
fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f\n', Tabl')
Для сигнала гусеничной техники:
Сводная таблица результатов
j aj bj nj pj npj
1 – Inf -0.09544 2 0.00000 0.01837
2 -0.09544 -0.09464 2 0.00000 0.00408
3 -0.09464 -0.09385 0 0.00000 0.00495
4 -0.09385 -0.09306 1 0.00000 0.00599
5 -0.09306 -0.09226 1 0.00000 0.00724
6 -0.09226 -0.09147 0 0.00000 0.00873
7 -0.09147 -0.09067 0 0.00000 0.01052
8 -0.09067 -0.08988 4 0.00000 0.01266
9 -0.08988 -0.08909 0 0.00000 0.01520
10 -0.08909 -0.08829 0 0.00000 0.01824
11 -0.08829 -0.08750 2 0.00000 0.02184
12 -0.08750 -0.08671 2 0.00000 0.02612
13 -0.08671 -0.08591 0 0.00000 0.03118
14 -0.08591 -0.08512 3 0.00000 0.03718
15 -0.08512 -0.08433 1 0.00000 0.04425
Для фонового сигнала:
Сводная таблица результатов
j aj bj nj pj npj
1 – Inf 0.01067 1 0.00000 0.00000
2 0.01067 0.01074 0 0.00000 0.00000
3 0.01074 0.01080 0 0.00000 0.00000
4 0.01080 0.01086 0 0.00000 0.00000
5 0.01086 0.01092 0 0.00000 0.00000
6 0.01092 0.01098 0 0.00000 0.00000
7 0.01098 0.01104 0 0.00000 0.00000
8 0.01104 0.01111 0 0.00000 0.00000
9 0.01111 0.01117 0 0.00000 0.00000
10 0.01117 0.01123 0 0.00000 0.00000
11 0.01123 0.01129 0 0.00000 0.00000
12 0.01129 0.01135 0 0.00000 0.00000
13 0.01135 0.01141 0 0.00000 0.00000
14 0.01141 0.01147 0 0.00000 0.00000
15 0.01147 0.01154 0 0.00000 0.00000
Если распределение подобрано, верно, то числа из 4-го и 6-го столбцов не должны сильно отличаться.
Вывод: Для сигнала гусеничной техники числа из 4-го и 6-го столбцов значительно отличаются, значит, распределение подобрано неверно. А для фонового сигнала эти числа практически совпадают.
Проверим выполнение условия npj ³ 5 и объединим те интервалы, в которых npj < 5. Перестроим таблицу и добавим в нее еще один, 7-й столбец – слагаемое, вычисляемое по выражению (21).
Практическая часть.
qz=0.3;% выбрали уровень значимости
ResTabl=Tabl (1,1:6);% взяли первую строку
for k1=2:k, % берем остальные строки таблицы
if ResTabl (end, 6)<5, % предыдущее npj<5 – будем суммировать
ResTabl (end, 3)=Tabl (k1,3);% новая правая граница интервала
ResTabl (end, 4:6)=ResTabl (end, 4:6)+Tabl (k1,4:6);% суммируем
|
|
|
else% предыдущее npj>=5 – будем дописывать строку
ResTabl=[ResTabl; Tabl (k1,1:6)];% дописываем строку
end
end
if ResTabl (end, 6)<5, % последнее npj<5
ResTabl (end – 1,3)=ResTabl (end, 3);% новая правая граница
ResTabl (end – 1,4:6)=ResTabl (end – 1,4:6)+ResTabl (end, 4:6);
ResTabl=ResTabl (1:end-1,:);% отбросили последнюю строку
end
kn=size (ResTabl, 1);% число объединенных интервалов
ResTabl(:, 1)=[1:kn]';% новые номера интервалов
ResTabl(:, 7)=(ResTabl(:, 4) – ResTabl(:, 6)).^2./ResTabl(:, 6);
disp ('Сгруппированная сводная таблица результатов')
fprintf (' j aj bj')
fprintf (' nj pj npj ')
fprintf([' (nj-npj)^2/npj\n'])
fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f % 12.5f\n', ResTabl')
hi2=sum (ResTabl(:, 7));% сумма элементов последнего столбца
fprintf(['Статистика Пирсона chi2=%10.5f\n'], hi2)
m=[3,2,3,2];% число ограничений
fprintf ('Задаем уровень значимости q=%5.4f\n', qz)
chi2qz=chi2inv (1-qz, kn-m(bdistr));% квантиль
fprintf(['Квантиль chi2-распределения Пирсона '…
'chi2 (1-q)=%10.5f\n'], chi2qz)
if hi2<=chi2qz,
disp ('Распределение подобрано верно, т. к. chi2<=chi2 (1-q)')
else
disp ('Распределение подобрано неверно, т. к. chi2>chi2 (1-q)')
end
Для сигнала гусеничной техники:
Сгруппированная сводная таблица результатов
j aj bj nj pj npj (nj-npj)^2/npj
1 – Inf -0.07004 58 0.00009 5.46033 505.53988
2 -0.07004 -0.06607 32 0.00011 6.16617 108.23348
3 -0.06607 -0.06369 17 0.00011 6.35867 17.80845
4 -0.06369 -0.06210 16 0.00010 5.89961 17.29233
5 -0.06210 -0.06051 16 0.00013 7.65444 9.09908
6 -0.06051 -0.05893 16 0.00017 9.87115 3.80530
7 -0.05893 -0.05813 9 0.00010 5.93889 1.57781
8 -0.05813 -0.05734 16 0.00012 6.71391 12.84370
9 -0.05734 -0.05655 12 0.00013 7.57856 2.57953
10 -0.05655 -0.05575 17 0.00015 8.54160 8.37603
11 -0.05575 -0.05496 15 0.00017 9.61240 3.01967
12 -0.05496 -0.05416 17 0.00019 10.80104 3.55773
13 -0.05416 -0.05337 13 0.00021 12.11825 0.06416
14 -0.05337 -0.05258 26 0.00024 13.57548 11.37115
15 -0.05258 -0.05178 20 0.00026 15.18487 1.52688
Статистика Пирсона chi2=2613.15423
Задаем уровень значимости q=0.3000
Квантиль chi2-распределения Пирсона chi2 (1-q)= 182.25040
Распределение подобрано неверно, т. к. chi2>chi2 (1-q)
Вывод: По критерию Пирсона распределение подобрано неверно, т. к. реальное значение статистики χ2р=2613.15423 намного превышает критическое значение χ2т,f=182.25040, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала не подтверждается на уровне значимости 0.05.
Для фонового сигнала:
Сгруппированная сводная таблица результатов
j aj bj nj pj npj (nj-npj)^2/npj
1 – Inf 0.01690 11 0.00026 7.51515 1.61596
2 0.01690 0.01702 13 0.00031 8.99732 1.78070
3 0.01702 0.01708 14 0.00026 7.55999 5.48594
4 0.01708 0.01714 15 0.00037 10.63561 1.79095
5 0.01714 0.01720 13 0.00052 14.78664 0.21588
6 0.01720 0.01727 24 0.00071 20.31617 0.66797
7 0.01727 0.01733 33 0.00097 27.58544 1.06279
8 0.01733 0.01739 35 0.00130 37.01551 0.10975
9 0.01739 0.01745 54 0.00172 49.08550 0.49205
|
|
|
10 0.01745 0.01751 58 0.00225 64.32627 0.62217
11 0.01751 0.01757 79 0.00291 83.30848 0.22282
12 0.01757 0.01764 102 0.00373 106.62418 0.20055
13 0.01764 0.01770 137 0.00472 134.86147 0.03391
14 0.01770 0.01776 167 0.00590 168.57212 0.01466
15 0.01776 0.01782 185 0.00729 208.23287 2.59213
Статистика Пирсона chi2= 57.37478
Задаем уровень значимости q=0.3000
Квантиль chi2-распределения Пирсона chi2 (1-q)= 66.27446
Распределение подобрано, верно, т. к. chi2<=chi2 (1-q)
Вывод: Для фонового сигнала по критерию Пирсона распределение подобрано верно, т. к. реальное значение статистики χ2р=609411.53699 не превышает критическое значение χ2т,f=520.15366, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала подтверждается.
|
|
|
