 |
Синус, косинус и тангенс острого угла прямоугольного треугольника
|
|
|
|
Тригонометрия.
В переводе с греческого: тригон – треугольник; метрио – измерять. То есть находить размеры сторон и углов треугольника. Изучение тригонометрии начинается с прямоугольного треугольника.
Прямоугольный треугольник (основные понятия)
| - прямой угол – угол гамма  ;
- острые углы – углы  (альфа) и  (бета)
- катеты - стороны, образующие прямой угол (стороны а и b);
- гипотенуза - сторона, лежащая против угла  (сторона с);
- катет, прилежащий к одному из острых углов;
- катет, противолежащий одному из острых углов
для  : катет а – противолежащий; катет b – прилежащий;
для  : катет b – противолежащий; катет a – прилежащий.
|
Соотношение углов: 
; 
;
Соотношение сторон: 
;
Синус и косинус острого угла прямоугольного треугольника
| Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. | 
|
| Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. | 
|
Из определений следует:
| Синус и косину двух разноимённых острых углов равны: | 
|
Числовые значения синуса и косинуса углов от 
можно найти с помощью калькулятора или в специальных таблицах (таблицы Брадиса).
Принятые обозначения в треугольнике
- прописными буквами латинского алфавита для сторон и греческими буквами для углов (обычно для сторон это  ; для углов –  (альфа),  (бета),  (гамма);
Синус и косинус углов: 
|
|
- заглавными буквами латинского алфавита для вершин и углов:
для ΔABC: вершина В и угол ∠В; вершина С и угол ∠С;
для ΔFNP: вершина F и угол ∠F; вершина N и угол ∠N и т.д.;
Синус и косинус углов: 
|  
|
- смежные углы треугольника обозначаются тремя буквами, причём в середине буква нужного угла.
Например, для ΔFPN:
∠NPH или ∠HPN; ∠PHN или ∠NHP.
Синус и косинус углов: 
| 
|
|
|
|
Примеры решения задач
Задача 1. В прямоугольном треугольнике с катетом 
и гипотенузой 
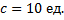
Найти градусную меру острых углов.
Решение: Строим указанный треугольник.
| 1) 
С помощью калькулятора или таблиц Брадиса определяем угол :
для  угол  .
2) Так как  , то 
Ответ:  .
|
Задача 2. В прямоугольном треугольнике ABC угол 
, 
, 
. Найти градусную меру угла А.
Решение: Строим указанный треугольник.
| Для угла А катет АС является прилежащим.
1) Воспользуемся формулой косинуса острого угла:
|
2) С помощью таблиц Брадиса или с помощью калькулятора находим для 
угол 
.
Ответ: 
.
Тангенс и котангенс острого угла прямоугольного треугольника
|
| Тангенсом острого угла называется отношение противолежащего катета к прилежащему
Котангенсом острого угла называется отношение прилежащего катета к противолежащему
|
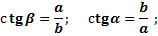
Из определений следует:
| Тангенс и котангенс взаимно обратны: |  ;
|
| Тангенс можно выразить через синус и косинус | 
|
Докажем последнее утверждение
Выразим из формул косинуса и синуса 
катеты 
и 
: 
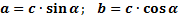
Тогда:
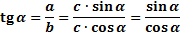
Числовые значения тангенса и котангенса углов от можно найти с помощью калькулятора или в специальных таблицах (таблицы Брадиса), а так же использовать значения синуса и косинуса одного и того же угла.
Пример решения задачи
Задача 3. В прямоугольном треугольнике KND ∠ 
, 
, 
.
Найти градусную меру угла, противолежащего к катету 
.
Решение: Строим указанный треугольник.
| Противолежащим для катета является угол D.
1) Воспользуемся формулой тангенса острого угла D:
2) С помощью калькулятора или таблиц Брадиса определяем угол  :
для  угол  .
Ответ:  .
|
|
|
|
Подготовка к проверочному тесту по теме
Синус, косинус и тангенс острого угла прямоугольного треугольника
Для любого обозначения прямоугольного треугольника нужно уметь:
- безошибочно определять гипотенузу, катеты, прилежащие и противолежащие стороны и углы;
- записывать формулы синуса, косинуса и тангенса острых углов;
- записывать теорему Пифагора;
- вычислять синус, косинус и тангенс острых углов с помощью таблиц Брадиса или калькулятора.
Варианты контрольного теста (самостоятельная работа)
--------------------------------------------------------------------------------------------------------------------------------------------------
Проверочный тест по теме «Тригонометрия прямоугольного треугольника» В.1
Постройте прямоугольный треугольник ADF, где 
Обозначьте на рисунке прямой угол.
Для данного треугольника укажите (запишите):
1) острые углы;
2) гипотенузу;
3) катеты;
4) катет, прилежащий к углу А;
5) катет, противолежащий углу F;
6) катет, прилежащий к углу F;
7) катет, противолежащий углу А;
8) формулу для определения 
| 9) формулу для определения 
10) формулу для определения 
11) формулу для определения 
12) формулу для определения 
13) формулу для определения 
14) теорему Пифагора;
15) градусную меру угла А, если 
16) градусную меру угла F, если 
|
--------------------------------------------------------------------------------------------------------------------------------------------------
Проверочный тест по теме «Тригонометрия прямоугольного треугольника» В.2
Постройте прямоугольный треугольник BKS, где 
Обозначьте на рисунке прямой угол.
Для данного треугольника укажите (запишите):
1) острые углы;
2) гипотенузу;
3) катеты;
4) катет, прилежащий к углу K;
5) катет, противолежащий углу S;
6) катет, прилежащий к углу S;
7) катет, противолежащий углу K;
8) формулу для определения 
| 9) формулу для определения 
10) формулу для определения 
11) формулу для определения 
12) формулу для определения 
13) формулу для определения 
14) теорему Пифагора;
15) градусную меру угла K, если 
16) градусную меру угла S, если 
|
--------------------------------------------------------------------------------------------------------------------------------------------------
|
|
|
