 |
Геометрическая интерпретация К.Ч. Комплексная плоскость.
|
|
|
|
Поле комплексных чисел
К.Ч. называется упорядоченная пара вещественных чисел: 
называются равными 
Введем две операции на множестве 
: 
(I) 
+ 
= 
=(
)
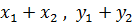(II) 
= 
(
)
Покажем, что ─ поле.
операция сложения (I)
2) ассоциативна:
3) существует нейтральный (нулевой) элемент 
: 
4) существует противоположный элемент 
:
Следовательно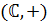 
– абелева группа
операция умножения (II) дистрибутивна относительно сложения
5) 
=(
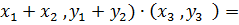
, аналогично проверяется дистрибутивность слева.
Следовательно – кольцо.
Операция умножения (II)
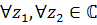
7) ассоциативна: (доказывается аналогично)
8) существует нейтральный элемент по умножению 
Следовательно – ассоциативное, коммутативное кольцо с единицей.
Осталось доказать, что существует обратный для 
Отступление.
Рассмотрим число вида 
, будем его отождествлять с числом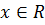 
, тогда сумма двух таких чисел
1) 
будет отождествляться с числом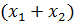 
,
т.е. с числом, которое мы получили бы при обычном сложении вещественных чисел 
,
их произведение
2) 
(
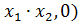
будет отождествляться с числом (
), т.е. с числом, которое мы получили бы при обычном умножении вещественных чисел .
Отсюда следует согласованность в определении сложения и умножения вещественных и комплексных чисел.
Далее будем отождествлять пару 
с вещественным числом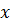 
. В частности будем считать 
.
Т.о. множество вещественных чисел R является подмножеством множества 
Пара 
мнимая единица (была введена Эйлером (1707- 1783), играет особую роль.
или 
Преобразуем произведение: 
Тогда 
алгебраическая форма записи К.Ч. удобна для сложения и умножения К.Ч.
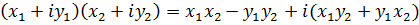
Комплексно сопряженные числа
· Каждому комплексному числу 
соответствует число 
, которое называется комплексно сопряженным числу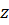 
.
|
|
|
· Любое действительное число равно своему сопряженному: 
Свойства комплексно сопряженных чисел
1) 
2) 
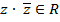
3) 
4) 
= 
⎕ 
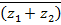5) 
= 
⎕ 
= 
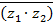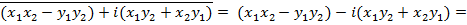
6) 
= 
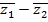
7) 
Два последних пункта доказываются аналогично.
9) Для того чтобы – было полем, осталось доказать, что
, 
обратный элемент 
такой что 
.
Заметим, что при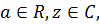 
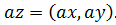Найдем выражение для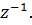 
⎕ Умножим равенство слева на 
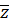
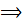
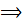
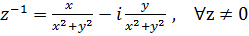
Следовательно, поле.
Будем называть 
вещественной частью; 
мнимой частью;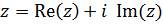 
Если 
, z – чисто мнимое число, если 
, z – вещественное число.
Частное можно получить, домножив числитель и знаменатель на число сопряженное знаменателю: 
:
Геометрическая интерпретация К.Ч. Комплексная плоскость.
Пусть на плоскости выбрана прямоугольная декартова система координат. Поставим в соответствие каждому комплексному числу 
точку 
этой плоскости. Очевидно, что это соответствие взаимно однозначно.
· вещественные числа изображаются точками оси абсцисс;
· на оси ординат располагаются изображения чисто мнимых чисел;
· началу координат соответствует число нуль;
· сопряженные комплексные числа изображаются точками симметричными относительно оси абсцисс.
· плоскость, точками которой изображаются К.Ч. называется к.п.;
· ее ось абсцисс- вещественной осью; ось ординат - мнимой осью.
Так как каждая точка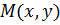 
плоскости связана с ее радиус-вектором 
, т.е. вектором, имеющим начало в точке О и конец в точке 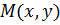, то К.Ч. можно изображать вектором .
Изображение комплексных чисел векторами позволяет дать простое геометрическое истолкование сложения и вычитания комплексных чисел.
При сложении комплексных чисел 
и 
складываются их действительные и мнимые части, а при сложении соответствующих им векторов 
и 
складываются их координаты. Поэтому сумме 
комплексных чисел будет соответствовать вектор 
, равный сумме векторов 
,
Относительно геометрического истолкования вычитания комплексных чисел, заметим, что вычитание векторов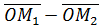 
сводится к сложению: 
в результате получаем вектор 
, соответствующий разности комплексных чисел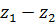 
.
|
|
|
· Геометрический смысл модуля разности комплексных чисел 
состоит в том, что он равен длине вектора | 
= 
, т.е. расстоянию между точками 
.
|
|
|
