 |
Определение и примеры чёткой логики
|
|
|
|
Определение и примеры чётких множеств
Чёткое множество – совокупность различных элементов, мыслимая как единое целое. X = { x }, x Є X
Операции над чёткими множествами:
- пересечение: 
- объединение: 
- разность (дополнение):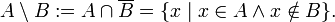 
- декартово произведение: 
Пусть множество цифр E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, тогда подмножество чётных цифр можно определить как: A = {0, 2, 4, 6, 8}.
Пусть множество фамилий E = {Иванов, Петров, Аносов, Кузнецов, Анискин, Афанасьев, Сергеев}, тогда подмножество фамилий, начинающихся на букву “А” можно определить:
A = {Аносов, Анискин, Афанасьев}.
Определение и примеры нечётких множеств
Универсальное множество – множество, содержащие все мыслимые объекты.
Нечёткое множество A – математический объект, представляющий собой множество, принадлежность к которому представляет собой не отношение, а функцию; совокупность универсального множества X и характеристической функции μA(x), которая характеризует степень принадлежности элемента x нечёткому множеству.
Функция μA(x) принимает значения в некотором линейно упорядоченном множестве принадлежностей M. Часто в качестве M выбирается отрезок [0, 1]. Если M = {0, 1}, то нечёткое множество может рассматриваться как обычное, чёткое множество.
Операции над нечёткими множествами:
- пересечение: 
- объединение: 
- сумма: 
- произведение: 
Пусть E = {1,2,3,...,100} и соответствует понятию " возраст ", тогда нечеткое множество " молодой ", может быть определено: m "молодой" (x) = 
. Нечеткое множество " молодой " на универсальном множестве E' ={ Иванов, Петров, Сидоров,...} задается с помощью функции принадлежности m" молодой " (x) на E = {1,2,3,..100} (возраст),называемой по отношению к E' функцией совместимости, при этом: m "молодой" (Сидоров):= m " молодой "(x), где x - возраст Сидорова.
|
|
|
Сходства чётких и нечётких множеств
Чёткие и нечёткие множества имеют одинаковую иерархию: они делятся на подмножества, множества и надмножества. Чёткие и нечёткие множества имеют одинаковые типы операций (Пересечение, объединение, произведение), производимые над ними.
Чёткое множество является частным случаем нечёткого, а понятие нечёткого множества является расширенным понятием, охватывающим и понятие чёткого множества.
Различия чётких и нечётких множеств
В чётком множестве все элементы делятся на 2 типа: относящиеся к нему и не относящиеся. Относительно элементов нечёткого множества можно говорить в какой мере они в него входят, а не просто входят они в него или нет. Операции над нечёткими множествами представляются отлично от операций над чёткими множествами.
Сравнение множеств происходит по разному:
Пусть A и B - 2 чётких множества, определённых на универсальном множестве X.
Множество A содержится во множестве B, если каждый элемент A есть элемент B:
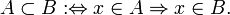
Два чётких множества называются равными, если они являются подмножествами друг друга: 
Пусть A и B нечёткие множества, заданные на универсальном множестве X. A содержится в B, если для любого элемента из X функция его принадлежности множеству A будет принимать значение меньшее либо равное, чем функция принадлежности множеству B:
В случае, если условие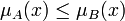 
выполняется не для всех 
, говорят о степени включения нечёткого множества A в B, которое определяется так:
Два нечётких множества называются равными, если они содержатся друг в друге:
2. Сравнительный анализ чёткой и нечёткой логики
Определение и примеры чёткой логики
Чёткая логика – детерминированная логика, допускающая только две оценки: истина и ложь. Она основана на двузначной булевой алгебре и чётких множествах.
|
|
|
Все переменные изменяются по базовому сигналу управления – тактовому импульсу.
С помощью чёткой логики можно строить последовательные схемы:
Для случая 1 входа и выхода существуют 4 операции отношения, для 2 входов и 1 выхода – 16 операций, и т.д.
| x | y | x ↓ y | x ← y | x | x → y | y | x ⊕ y | x | y | x & y | x ≡ y | y | x → y | x | x ← y | x ∨ y | ||
Среди них наиболее важными операциями являются НЕ-И и НЕ-ИЛИ, так как любую комбинаторную схему можно построить только с помощью только вентилей НЕ-И, либо – НЕ-ИЛИ.
В общем случае при логических выводах в искусственном интеллекте выполняется силлогизм, в основе которого лежат операции импликации. Его можно представить следующими формулами:
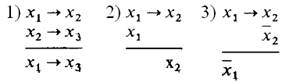
1) Вывод из утверждений “Если птица, то летает” и “Если летит, то направляется на этот остров” заключения “Если птица, то направляется на этот остров”.
2) Вывод из утверждений “Если птица, то летает” и “Это животное – птица” заключения “Это животное летает”.
3) Вывод из утверждений “Если птица, то летает” и “Это животное не летает” заключения “Это животное – не птица”.
|
|
|
