Удаление звена из произвольного места списка, отличного от начала (после звена, указатель на которое задан)

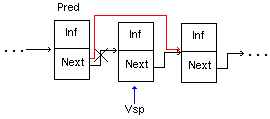
{Процедура удаления звена из списка после звена, на которое ссылается указатель Pred; в x содержится информация из удалённого звена} Procedure Iz_Spiska(Pred: U; Var X: BT); Var Vsp: U; Begin Vsp:= Pred^.Next; {Забираем ссылку на удаляемое звено} {Удаляем звено из списка, перенаправив ссылку на следующее за ним звено} Pred^.Next:= Pred^.Next^.Next; X:= Vsp^.Inf; {Забираем информацию из удаляемого звена} Dispose(Vsp); {Уничтожаем звено} End;

17. Бинарные деревья (основные понятия)

Определение:

 

Бинарное (двоичное) дерево (binary tree) - это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла.

 

Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева.

Узел дерева, не имеющий потомков, называется листом.

Схематичное изображение бинарного дерева:

Бинарное дерево может представлять собой пустое множество, и может выродиться в список. Вырожденное бинарное дерево:

Операции над бинарными деревьями

Бинарное дерево должно реализовывать следующие операции:

1. Инициализация бинарного дерева:
текущий указатель устанавливается неопределенным (или нулевым, nil), а количество узлов нулевым.

2. Помещение в бинарное дерево элемента:
для нового элемента в бинарном дереве создается соответствующий узел, указатели на потомков которого пусты (поиск позиции для такого узла начинается с корня и проходит согласно правилам, определяющим структуру бинарного дерева).

3. Получение значения текущего элемента

4. Поиск заданного элемента:
если искомый элемент находится в дереве, то возвращается указатель на него, в противном случае возвращается nil, сигнализирующий о неуспехе поиска значения

5. Удаление узла из дерева

6. Уничтожение бинарного дерева

 

Рассмотрим эти операции более подробно:

1. Структура для создания корня и узлов дерева имеет вид:

2. type3. T = Integer; { скрываем зависимость от конкретного типа данных }4. 5. TTree = ^TNode;6. TNode = record7. value: T;8. Left, Right: TTree; end;

Здесь поля Left и Right - это указатели на потомков данного узла, а поле value предназначено для хранения информации.

9. Удаление узла бинарного дерева.

Это немного более сложная операция, чем поиск заданного элемента. Сначала необходимо найти элемент, подлежащий удалению. Если этот элемент - лист, он может быть просто удален. Если же он является внутренним узлом (имеет потомков), то просто так удалить его не получится - будут разрушены внутренние связи в дереве.

Поступаем так:

o если удаляемый узел имеет только одного "сына", то его значение можно заменить значением этого "сына"

o если у удаляемого элемента 2 "сына", заменяем его элементом с наименьшим значением среди потомков правого "сына" (или элементом с наибольшим значением среди потомков левого "сына")

 

Для реализации процедуры Remove желательно иметь функцию DeleteMin, которая будет удалять наименьший элемент непустого дерева Root, и возвращать значение удаленного элемента:

function DeleteMin(var Root: TTree): T;var WasRoot: TTree;begin if Root^.Left = nil then begin DeleteMin:= Root^.value; { Результат функции } WasRoot:= Root; { Запоминаем узел для последующего удаления } Root:= Root^.Right; { продвигаемся дальше } Dispose(WasRoot); { удаляем бывший корень } end else { узел Root имеет левого "сына" } DeleteMin:= DeleteMin(Root^.Left); end;

Теперь процедура Remove может быть реализована так:

10. Уничтожение бинарного дерева.

11. Procedure Delete(T: TTree);12. Begin13. If T = nil Then Exit;14. 15. Delete(T^.Right);16. Delete(T^.Left);17. Dispose(T) End;

Обход дерева

Прохождение (или обход) бинарного дерева означает систематическое перечисление всех узлов для выполнения необходимой функциональной обработки. Наиболее известны и практически важны 3 способа прохождения, которые отличаются порядком и направлением обхода бинарного дерева. Можно проходить узлы в прямом порядке (сверху-вниз), в симметричном порядке (слева-направо) и, наконец, в концевом порядке (снизу-вверх).

Рекурсивные алгоритмы прохождения бинарного дерева по каждому из перечисленных способов включают 3 одинаковых процедуры, где нужно пройти корень поддерева, левое поддерево текущего корня и правое поддерево текущего корня. Направление обхода однозначно определяет последовательность выполнения указанных процедур. Последовательность их рекурсивного вызова для каждого способа прохождения перечислена в следующей таблице.

 

Таблица рекурсивных алгоритмов прохождения бинарного дерева-------------------------------------------------------------------------------- Порядок прохождения-------------------------------------------------------------------------------- Прямой | Симметричный | Концевой--------------------------------------------------------------------------------1. Корень поддерева |1. Левое поддерево |1. Левое поддерево2. Левое поддерево |2. Корень поддерева |2. Правое поддерево3. Правое поддерево |3. Правое поддерево |3. Корень поддерева--------------------------------------------------------------------------------

1. Прямой порядок прохождения означает обход в направлении сверху-вниз, когда после посещения очередного разветвления продолжается прохождение вглубь дерева, пока не пройдены все потомки достигнутого узла. По этой причине прямой порядок прохождения часто называют нисходящим, или прохождением в глубину.

Прямой порядок есть наиболее естественный способ перечисления узлов дерева в форме вложенных скобок или уступчатого списка. Если исключить все скобки и запятые, то последовательность узлов в форме вложенных скобок будет соответствовать прямому порядку прохождения дерева.

Уступы в ступенчатом списке, представляющем любую иерархическую структуру, также располагаются в прямом порядке. В генеалогических терминах прямой порядок прохождения дерева отражает династический порядок престолонаследования, когда титул передается старшему потомку.

2. При симметричном порядке дерево проходится слева-направо, порождая лексиграфически упорядоченную последовательность ключей узлов. По этой причине симметричный порядок прохождения часто называют лексиграфическим. Симметричность порядка выражается в том, что если бинарное дерево отразить относительно вертикальной оси, поменяв местами левые и правые узлы, то симметричный порядок прохождения заменится на противоположный лексиграфический.

1. Если применяется концевой порядок прохождения, то получается обход дерева снизу-вверх, когда в момент посещения любого узла все его потомки уже пройдены, а корень дерева проходится последним. Из-за этой особенности обхода, концевой порядок часто называют восходящим, или обратным относительно прямого.
   
   При выборе определенного порядка прохождения требуемая функциональная обработка каждого узла происходит после соответствующего числа заходов в него. При обходе сверху-вниз каждый узел обрабатывается при первичном заходе в него, при симметричном порядке прохождения - во втором, а при обходе снизу-вверх - в третьем.
   
   
   Еще один вариант обхода - по уровням: сначала выводить корень, потом - все узлы первого уровня, за ними - узлы второго уровня, и т.д.
   
   Это реализуется вот такой процедурой:

procedure PrintByLevel(level: integer; var items: array of TTree; count: integer);var i, new_count: integer;begin if count <> 0 then begin writeln('level = ', level); new_count:= 0; for i:= 0 to pred(count) do begin write(items[i]^.value:4); if items[i]^.left <> nil then begin inc(new_count); items[count + new_count - 1]:= items[i]^.left; end; if items[i]^.right <> nil then begin inc(new_count); items[count + new_count - 1]:= items[i]^.right; end; end; writeln; move(items[count], items[0], new_count*sizeof(TTree)); PrintByLevel(level + 1, items, new_count); end;end; http://alfa47.narod.ru/pascale.htm#37http://nikki.am9.ru/programming/languages/pascal/?page=Chapter%202/1.htm#12

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: