 |
Установка нивелира в рабочее положение
|
|
|
|
Нивелирование: цели, задачи, виды
Нивелир-ние-вид геодез измер,в рез кот опр превыш точек и их высоты над уровенн поверхн. Виды: 1)геометрич –превыш опр с пом горизонт луча визир-ния (для этого исп нивелир) с использ спец нивелирн реек.2)Тригонометрич-с пом наклонного луча визир,т.е. с пом теодолита.(при этом измер угол наклона и расст между 2 т).3)Физическое-при кот превыш опр с использ физич приёмов.(физич нивелиры: гидростатич,барометрич и радиолакционные).4)Автоматич-с пом спец техники,кот устанавл на автомобиль.(исп при нивелир дорог). При изучении фигуры Земли высоты точек земной поверхности определяют не над уровнем моря, а относительно поверхности референц-эллипсоида и применяют методы астрономического или астрономо-гравиметрического нивелирования. Нив-ние произв для изуч форм рельефа, опр высот точек при проектир, стр-ве и эксплуатац разл инженерн сооруж. Рез-ты нивелир-ния имеют большое знач для реш научных задач как самой геодезии, так и др наук о Земле.
Абсолютные и относительные высоты
Абсолютная высота - высота любой точки земной поверхности над уровнем океана. Она бывает положительной (местность лежит выше уровня океана) и отрицательной (местность расположена ниже уровня океана). Положительную абсолютную высоту имеет большая часть суши. В России абсолютные высоты отсчитываются от уровня Балтийского моря у Кронштадта. Относительная высота - это превышение одной точки земной поверхности над другой. Она показывает, на сколько одна точка земной поверхности расположена выше или ниже другой. Абсолютные и относительные высоты характеризуют расчлененность рельефа.
Геометрическое нивелирование: цели, задачи
|
|
|
Геометрическое нивелирование производится горизонтальным визирным лучом, который получают чаще всего при помощи приборов, называемых нивелирами. Точность геометрического нивелирования характеризуется средней квадратической погрешностью нивелирования на 1 км двойного хода равной от 0.5 до 10.0 мм в зависимости от типа используемых приборов
Способы геометрического нивелирования
Геометрическое нивелирование выполняется горизонтальным лучом визирования. Перед нивелированием точки на местности закрепляют колышками, костылями, башмаками, на которые устанавливают вертикально нивелирные рейки. Место установки нивелира для работы называют станцией, а расстояние от нивелира до рейки - плечом нивелирования.

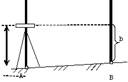
Рис.30. Способы геометрического нивелирования: а - из середины; б – вперед
Различают два способа геометрического нивелирования: из середины и вперед. При нивелировании из середины (рис.30а) нивелир устанавливается примерно на равных расстояниях от реек, поставленных на точки А и В, а превышение вычисляют по формуле:
h = a - b,
где а и b - отсчеты в мм по рейкам, установленным соответственно на задней по ходу движения при нивелировании и передней точках.
Знак превышения h получится положительным, если а больше b, и отрицательным, если а меньше b. Если известна высота НА задней точки А, то высота передней точки В
НВ = НА + h.
При нивелировании вперед нивелир ставят так, чтобы его окуляр находился над точкой А, измеряют высоту прибора i, затем визируя на рейку, отвесно поставленную в точке В, берут отсчет b. В этом случае:
h = i - b.
При нивелировании нескольких точек для вычисления их высот используют горизонт прибора, которым называют высоту горизонтальной линии визирования, т.е. горизонт прибора равен высоте точки, на которой установлена рейка, плюс отсчет по рейке. Из рис. 30 б следует:
|
|
|
ГП = HA + i; НB = ГП - b.
Последовательное нивелирование применяется для измерения превышений между точками А и D, разделенными значительным расстоянием или превышениями.
Нивелирование вперёд
При нивелировании вперед нивелир ставят так, чтобы его окуляр находился над точкой А, измеряют высоту прибора i, затем визируя на рейку, отвесно поставленную в точке В, берут отсчет b. В этом случае:
h = i - b.
При нивелировании нескольких точек для вычисления их высот используют горизонт прибора, которым называют высоту горизонтальной линии визирования, т.е. горизонт прибора равен высоте точки, на которой установлена рейка, плюс отсчет по рейке.

ГП = HA + i; НB = ГП - b.
Последовательное нивелирование применяется для измерения превышений между точками А и D, разделенными значительным расстоянием или превышениями.

а - из середины;
Нивелирование из середины
При нивелировании из середины (рис.30а) нивелир устанавливается примерно на равных расстояниях от реек, поставленных на точки А и В, а превышение вычисляют по формуле:
h = a - b,
где а и b - отсчеты в мм по рейкам, установленным соответственно на задней по ходу движения при нивелировании и передней точках.
Знак превышения h получится положительным, если а больше b, и отрицательным, если а меньше b. Если известна высота НА задней точки А, то высота передней точки В
НВ = НА + h.
Установка нивелира в рабочее положение
Для установки нивелира в рабочее положение его закрепляют на штативе становым винтом и вращением сначала двух, а затем третьего подъемных винтов приводят пузырек круглого уровня на середину. Отклонение пузырька от середины допускается в пределах второй окружности. В этом случае диапазон работы элевационного винта позволит установить пузырек цилиндрического уровня в нульпункт и установить визирную ось зрительной трубы в горизонтальное положение при соблюдении главного условия (для нивелира с цилиндрическим уровнем UU1 WW1). Приближенное наведение на нивелирную рейку выполняют с помощью мушки, расположенной сверху зрительной трубы. Более точное наведение осуществляют вращением наводящего винта зрительной трубы, которую перед отсчетом по рейке предварительно устанавливают по глазу (вращением окуляра) и по предмету (вращением кремальеры) для четкого совместного изображения сетки нитей и делений на нивелирной рейке. Перед отсчетом по средней нити тщательно совмещают концы пузырька цилиндрического уровня в поле зрения трубы, медленно вращая элевационный винт.
|
|
|
|
|
|
12 |


