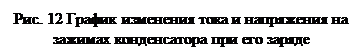Энергия электрического поля. Заряд и разряд конденсатора

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

 

Процесс заряда конденсатора заключается в разделении заря­дов, т. е. создании на одной пластине избытка зарядов одного знака, а на другой пластине — другого знака.

 

Если соединить металлическим проводником пластины заряжен­ного конденсатора, то противоположные по знаку электрические заряды, накопленные на пласти­нах, теперь воссоединяются. На­ступает разряд конденсатора. Элек­трическое поле исчезает.

 

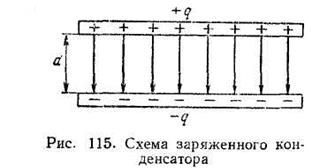
На рис. 9 схематически по­казан плоский заряженный кон­денсатор.

 

 

Пусть расстояние ме­жду пластинами d будет мало и поэтому электрическое поле между пластинами будем считать однородным. Как нам известно, для однородного поля между напряже­нием и напряженностью поля существует следующая зависимость:

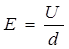
Учитывая, что для плоского конденсатора

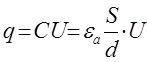или

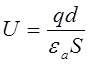
получим

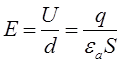
Отсюда следует, что если изменить расстояние между пласти­нами, то величина заряда пластин не изменится и напряженность поля также не изменится.

 

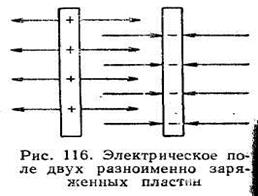
Напряженность электрического поля конденсатора Е можно рассматривать как сумму напряженностей Е₁ и Е₂, обусловленных зарядами двух заряжен­ных пластин:

Е = Е₁ + Е₂,

так как векторы напряженностей разно­именно заряженных пластин в простран­стве между ними имеют одно направ­ление (рис. 10).

 

 

 

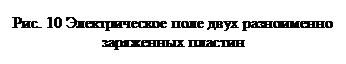Но Е₁ = Е₂, поэтому

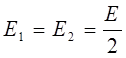
Разноименные заряды пластин взаимно притягиваются друг к другу. Сила взаимодействия зависит от величины заряда каждой из пластин и от величины напряженности поля. Так как при изменении расстояния между пластинами величина заряда пластин и величина напряженности поля остаются постоянными, то величина силы взаимодействия между пластинами тоже остается постоянной. Сила, действующая на вторую пластину со стороны первой пластины,

F = E₁·q,

будет равна силе, действующей на первую пластину со стороны второй пластины,

F = E₂·q,

Таким образом,

F = E₁·q = E₂·q =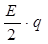

Раздвигая пластины конденсатора от расстояния, равного нулю, до расстояния, равного d, будем совершать работу

A = F·d,

идущую на преодоление силы взаимодействия между пластинами конденсатора.

Работа эта будет равна

A = F · d =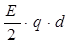

Так как , то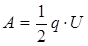

Учитывая, что q = C ·U, получим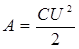

Механическая работа А, совершаемая при раздвижении пла­стин на основании закона сохранения энергии, должна быть равна
количеству энергии W_Э, запасенной в электрическом поле конден­сатора, т. е.     

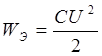
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА

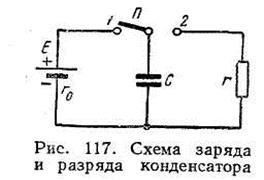
Составим электрическую цепь, изображенную на рис. 11.

 

 

Если переключатель П поставить в положение 1, незаряженный конден­сатор емкостью С оказывается подсоединенным к источнику элек­трической энергии, э. д. с. которого Е и внутреннее сопротивле­ние r₀. Начнется процесс заряда конденсатора. На пластинах кон­денсатора будут накапливаться равные по величине количества электричества: положительного — на одной пластине и отрица­тельного — на другой. Для накопления заряда на пластинах тре­буется определенное время, в течение которого по соединительным проводам будет проходить зарядный ток.

По мере накапливания зарядов на пластинах конденсатора вели­чина зарядного тока будет уменьшаться, а напряжение между пла­стинами конденсатора будет плавно увеличиваться. Когда напряжение конденсатора станет равным э. д. с. источника энергии, зарядный ток прекра­тится. В электрическом поле конденсатора за счет энергии внешнего источника будет запасена энергия .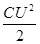

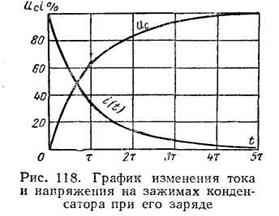
На рис. 12 представлен график изме­нения тока и напряжения на зажимах кон­денсатора при его заряде.

 

Теоретически процесс заряда конденсатора протекает бесконечно долго, но практически его можно считать законченным за время

t = (4…5) τ =(4…5) r · С,

где τ , называемая постоянной времени, представляет собой про­изведение r · С  иизмеряется в секундах: τ = rС,

Если переключатель П схемы на рис. 12 перевести в положе­ние 2, то заряженный конденсатор будет разряжаться через сопротивление r. Напряжение между пластинами конденсатора создаст в цепи ток разряда. Конденсатор разряжается сначала быстро, а затем все медленнее и медленнее. Напряжение между зажимами конденсатора и ток разряда будут уменьшаться от максимального значения до нуля.

Энергия, запасенная в электрическом поле конденсатора, при разряде выделяется в виде тепла в сопротивлении r.

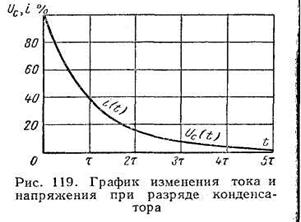
График изменения напряжения на зажимах конденсатора и тока разряда при разряде конденсатора показан на рис. 13.

  Как заряд, так и разряд конденсатора теоретически протекают бесконечно долгое время. Практически разряд прекращается за время

t = (4…5) τ

 

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: