Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Совместная работа студента с преподавателем - 5 мин

Тема № 11. Кибербезопасность.

Цель: Изучить комплекс проблем информационной безопасности предпринимательских структур различных типов и направлений деятельности, построения, функционирования и совершенствования правовых, организационных, технических и технологических процессов, обеспечивающих информационную безопасность и формирующих структуру системы защиты ценной и конфиденциальной информации в сферах охраны интеллектуальной собственности предпринимателей и сохранности, их информационных ресурсов. Осуществить минимизацию потерь, вызванных нарушением целостности или конфиденциальности данных, а также их недоступности для потребителей. Освоить основные понятия криптологии и шифрования.

 

Задачи обучения: Овладение теоретическими, практическими и методическими вопросами обеспечения информационной безопасности и освоение системных комплексных методов защиты предпринимательской информации от различных видов объективных и субъективных угроз в процессе ее возникновения, обработки, использования и хранения. Методы криптографического преобразования данных.

 

Организационная часть - 5 мин

Перекличка студентов и выяснение причин отсутствия студентов, кто не готов к занятию, проверка конспектов.

 

Количество формируемых компетенций: практические навыки и правовые навыки.

Методы обучения и преподавания: информационные технологии обучения.

Методы контроля формируемых на занятии компетенций:

ü тестирование проводится в компьютерной форме (студент должен ответить на «тест», содержа­щий в себе минимальные знания и навыки – основные определения, теоретические вопросы дан­ной темы). Устный опрос (студент обязан приходить на занятия подготовленным по данной теме, по вопро­сам указанным в методических указаниях), решение ситуационных задач (студент должен выполнить индивидуаль­ное задание для получения определенных навыков по решению типовых задач);

ü оценка правовой компетенций проводится в виде письменного опроса.

Самостоятельная работа студентов - 30 мин

Освоение практических навыков: Решение ситуационных задач.

Задания:

Шифр Цезаря

Реализует следующее преобразование открытого текста: каждая его буква заменяется третьей после нее буквой в алфавите, который считается написанным по кругу, т.е. для русского алфавита4)после буквы я следует буква а:

a б в г … ь э ю я
…
г д е ё … я а б в

Если закодировать буквы русского алфавита числами в десятичном представлении:

a б в г д е ё ж з и й к л м н о п р с т у ф х ц ч ш щ ъ ы ь э ю я
                                                                 

то шифр Цезаря можно представить в виде функции

где 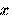— номер буквы открытого текста в алфавите. Здесь число 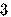указывает величину сдвига алфавита; понятно, что она могла быть выбранной любой:

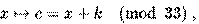
лишь бы только число было известно адресату. Дешифрование им полученного текста производится «сдвигом» в противоположную сторону:

Здесь означает номер буквы шифровки в алфавите. Шифр Цезаря относится к классу шифров замены. Тривиальный шифр замены: буква произвольный (фиксированный) символ «взламывается» частотным анализом достаточно длинного шифрованного сообщения. Известна Частота встречаемости букв в обычном (неспециальном) тексте (без учета пробелов):

a б в г д е,ё ж з и й к л м н о п Р с т
0.075 0.017 0.046 0.016 0.03 0.087 0.009 0.018 0.075 0.012 0.034 0.042 0.031 0.065 0.110 0.028 0.048 0.055 0.065
у ф х ц ч ш щ ъ,ь ы э ю я              
0.025 0.002 0.011 0.005 0.015 0.007 0.004 0.017 0.019 0.003 0.007 0.022              

Следовательно, имеет смысл посчитать количества совпадающих символов в шифровке и ранжировать полученное: наиболее часто встречаемый символ, скорее всего, соответствует букве5) о, следующий по частоте — возможно, букве е и т.д.

На всякий случай, я поставил собственный эксперимент, результаты которого можно посмотреть ☞ ЗДЕСЬ. Статистику для некоторых книг можно найти ☞ ЗДЕСЬ. Кажется, что при переходе от века XIX-го к XX-му частота встречаемости буквы а постепенно становится выше, чем е …

?

Дешифруйте:

NEGJVEGHJUHFVVBCNEBRKFDBFNEHFYTGJVJUFTN.

Открытый текст представляет собой фразу на русском языке. Можно повысить безопасность шифра Цезаря, сделав величину контекстно зависимой, т.е. зависящей от места буквы в открытом тексте.

 

Шифр Виженера

как раз и реализует это. Для шифрования некоторого сообщения, например:

OБ АЛГЕБРАИЧЕСКИХ ПРЕОБРАЗОВАНИЯХ выбираем произвольное сочетание букв, скажем, КРИПТО, которое предполагается секретным для всех, кроме адресата. Буква сообщения сдвигается по алфавиту на величину, равную порядковому номеру в алфавите соответствующей буквы секретного слова:

15 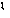0 3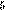
О Б А Л Г Е Б Р А И Ч Е С К И Х П Р Е О Б Р А З О В А Н И Я Х
К Р И П Т О                                                  
11 9 19                                                  
Щ С И Ы Х У                                                  
26 9 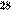22                                                  

Итак, первые 6 букв сообщения зашифрованы. Как поступить с оставшимися? Можно зашифровать их с помощью того же секретного слова:

            1 0 24 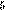18 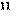9 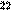16 5 1 0 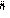15 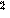0 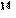9 22  
О Б А Л Г Е Б Р А И Ч Е С К И Х П Р Е О Б Р А З О В А Н И Я Х открытый текст
К Р И П Т О К Р И П Т О К Р И П Т О К Р И П Т О К Р И П Т О К  
            11 9 19 11 9 19 11 9 19 11 9 19 11  
Щ С И Ы Х У Л Б И Ш Й У Ь Ы С Е В Я П Я Й А Т Ц Щ Т И Э Ы Н А шифровка
            12 9 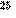43 29 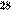18 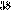35 16 10 19 26 9 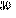28 33  
                                                 

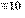
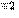
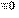
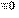
Аналитическое задание этого шифра:

где , а число определяется как номер 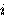-й буквы секретного слова в алфавите. Ту же формулу можно записать в еще более компактном виде

Для дешифрования получателю достаточно применить обратное преобразование:

т.е. ему необходимо знать либо секретное шифрующее слово, либо же дешифрующее слово, образованное как раз из букв, соответствующих числам , т.е. ХПЧРНС:

26 9 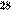22 12 9 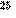43 29 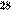18 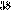35 16 10 19 26 9 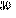28 33
Щ С И Ы Х У Л Б И Ш Й У Ь Ы С Е В Я П Я Й А Т Ц Щ Т И Э Ы Н А
Х П Ч Р Н С Х П Ч Р Н С Х П Ч Р Н С Х П Ч Р Н С Х П Ч Р Н С Х
22 24 14 22 24 14 22 24 14 22 24 14 22 24 14 22
О Б А Л Г Е Б Р А И Ч Е С К И Х П Р Е О Б Р А З О В А Н И Я Х
15 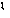0 3 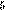1 0 24 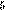18 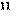9 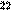16 5 1 0 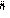15 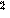0 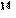9 22

Фактически шифр Цезаря является вырожденным, частным случаем шифра Виженера, когда секретное слово тривиально состоит из одной только буквы г. Другая крайность заключается в использовании достаточно длинной секретной фразы:

            1 0 24 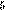18 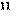9 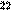16 5 1 0 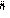15 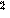0 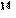9 22  
О Б А Л Г Е Б Р А И Ч Е С К И Х П Р Е О Б Р А З О В А Н И Я Х  
К Р И П Т О Г Р А Ф И Я Д О Л Ж Н А Б Ы Т Ь Э К О Н О М Н О Й секретная фраза
            3 0 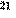9 4 12 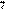14 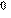1 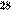19 30 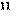15 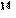15 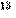14 10  
Щ С И Ы Х У Д Б А Э А Д Х Щ Ф Ь Э Р Ё Й У М Э Т Э П О Ъ Ц Н Я шифровка
            4 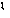0 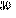0 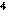22 21 30 6 20 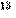30 30 15 23 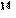32  

А для шифрования длинного сообщения можно взять отрывок из какой-нибудь книги. Понятно, что законный получатель шифровки должен знать и книгу, и место, с которого ему надо осуществить «привязку» отрывка текста к шифровке. И хотя такой подход кажется очень трудоемким, не будем отметать его сходу.

 

Шифр Кардано

Приписывается итальянскому математику, астрологу, медику и мистику Кардано. Шифр можно рассматривать как вариант шифра Виженера, и начальная стадия у них одинакова: первые буквы отрытого текста шифруются с помощью секретного слова. Остроумие идеи Кардано заключается в том, что шифрование оставшейся части текста осуществляется с помощью самого этого текста:

15 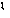0 3 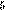1 0 24 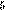18 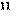9 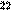16 5 1 0 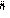15 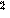0 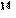9 22  
О Б А Л Г Е Б Р А И Ч Е С К И Х П Р Е О Б Р А З О В А Н И Я Х открытый текст
К Р И П Т О О Б А Л Г Е Б Р А И Ч Е С К И Х П Р Е О Б Р А З О секретное слово & открытый текст
            15 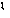0 3 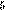1 0 24 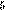18 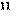9 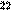16 5 1 0 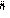15  
Щ С И Ы Х У П С А Ф Ъ Й Т Ы И Ю Ж Х Ц Щ Й Ё П Ш У Р Б Ю И Ж Д шифровка
            16 0 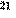27 19 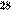9 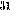7 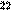23 10 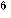16 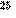20 1 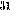9 4  

В самом деле, только зная секретное слово КРИПТО можно восстановить первые 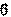букв сообщения, с их помощью можно восстановить следующие 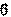букв и т.д.

Под ключом в криптографии понимают сменный элемент шифра, который применяется для шифрования или дешифрования конкретного сообщения. Например, в шифре Цезаря ключом является — величина сдвига алфавита, в шифре Виженера — секретное слово или фраза.

Во всех приведенных выше примерах процесс шифрования оказалось удобным описывать посредством предварительной операции над буквами открытого текста — их представлением в виде чисел. Сама процедура такой замены буква символ (совокупность символов) называется кодированием. С формальной точки зрения кодирование можно рассматривать как частный случай шифрования (см. шифр замены). Однако в современной криптографической литературе эти две операции принято различать по целям их применения: шифрование предназначено для скрытия информации, в то время как кодирование — для удобства ее хранения и передачи. Например, для передачи информации по каналу связи, подверженному воздействию помех (шумов), используются коды, исправляющие ошибки, когда символы сообщения представляются такими цепочками битов, чтобы «порча» любого бита (или фиксированного числа битов) при передаче не помешала получателю однозначно восстановить (декодировать) передаваемый символ.

В дальнейшем мы будем часто использовать кодировку, которую назовем стандартной:

а б В г д е,ё ж з и й к л м н о п р с т у ф х ц ч ш щ ъ ы ь э ю я
                                                               
пробел
                                                               

Итак, шифрование можно представить как некоторую операцию над числами кодировки. И собственно ключ также может быть выражен в виде числа. Оптимальным был бы абсолютно непредсказуемый, случайный выбор последовательности цифр ключа — тогда перехвативший шифровку злоумышленник не сможет предугадать закон формирования его элементов. Если иметь в виду соображения удобств технической реализации, то и числа кодировки и ключ следует представлять не в десятичной, а в двоичной системе; иначе говоря, объектами корреспонденции становятся последовательности из нулей и единиц. При шифровании каждый бит открытого текста преобразуется в бит шифротекста по некоторому правилу с использованием битов ключа.

Шифр Вернама ("одноразового блокнота")

Вернам предложил использовать для шифрования преобразование

где 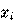представляет бит открытого текста, а — бит ключа; при этом последовательность битов ключа формируется случайным образом. Будем использовать обозначение 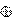для операции побитного сложения по модулю чисел, представленных в двоичной системе счисления (XOR): если и 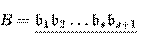два числа, представленных в такой системе, то

Таким образом:

и

                                                            … открытый текст
                                                            … ключ
                                                            … шифровка

Законный адресат (получатель шифровки) должен иметь в своем распоряжении дубликат ключа, т.е. фактически ему должна быть заранее передана последовательность битов, не меньшая (по длине) возможной шифровки. Подобное решение проблемы конфиденциальности переписки на первый взгляд кажется порочным кругом: для соблюдения секретности передаваемого сообщения необходимо предварительно передать корреспонденту по абсолютно надежному каналу ключ той же длины. Но противоречие это только кажущееся: на самом деле секрет «разделяется». Ключ передается корреспонденту с надежным курьером — например, с офицером дипломатической почты. После одноразового использования ключа для шифрования и дешифрования сообщения, ключ уничтожается. В случае перехвата курьера потенциальный противник получит в свое распоряжение лишь бессмысленный набор символов, и тогда ключ просто меняется на другой; опасность же возможного копирования ключа (посредством подкупа курьера) может быть заблокирована техническими средствами… Шифр «одноразового блокнота» считается абсолютно надежным, и, по некоторым данным, именно им до последнего времени обеспечивалась секретность канала «горячей линии» между Кремлем и Белым Домом.

Для шифра Вернама ключ дешифрования совпадает с ключом шифрования; так, для приведенного примера получаем:

                                                            … шифровка
                                                            … ключ
                                                            … открытый текст

Литература:

1. Основы информационной безопасности: учеб. пособие / Ю.Г. Крат, И.Г. Шрамкова. – Хабаровск: Изд-во ДВГУПС, 2008. –112 с.

2. Блинов А. М. Информационная безопасность: Учеб. пособие. Часть 1 / А. М. Блинов.–СПб.: СПБГУЭФ, 2010. – 96 с.

3. Информационная безопасность: Учебник для студентов вузов. — М.: Академический Проект; Гаудеамус, 2-е изд. — 2004. — 544 с.

4. Гатчин Ю. А., Сухостат В. В. Теория информационной безопасности и методология защиты информации. — СПб.: СПбГУ ИТМО, 2010. — 98 с.

5. Макаренко С. И. Информационная безопасность: учебное пособие для студентов вузов. — Ставрополь: СФ МГГУ им. М. А. Шолохова, 2009. — 372 с.

6. Павел Исаев. Некоторые алгоритмы ручного шифрования (рус.) // Компьютер Пресс. — 2003. — Вып. 3.

7. Жельников В. Появление шифров // Кpиптография от папируса до компьютера. — М.: ABF, 1996. — 335 с.

8. Дориченко С. А., Ященко В. В. 1.4 Криптография как искусство. Немного истории. // 25 этюдов о шифрах: Популярно о современной криптографии. — М.: Теис, 1994. стр. 14-18. (Математические основы криптологии).

9. Скляров Д.В.. 6.2 Литература по криптологии // Искусство защиты и взлома информации. — СПб.: БХВ-Петербург, 2004. 288 с. - 3000 экз.

10. Коробейников А.Г., Гатчин Ю. А. 1.2 Из истории криптографии // Математические основы криптологии. — СПб.: СПб ГУ ИТМО, 2004. — стр. 10-13.

11. Носов.В.А. Краткий исторический очерк развития криптографии (рус.) (18 октября 2002). Проверено 10 декабря 2009. Архивировано из первоисточника 26 января 2011.

12. Андрей Винокуров. «Криптография, ее истоки и место в современном обществе» (Цикл статей по криптографии. Введение)

13. Брюс Шнайер - статья «Почему криптография сложнее, чем кажется» (журнал «Компьютера» №34 от 10 сентября 1998 года)

14. Сергей Баричев «Основной вопрос криптографии» (журнал «CIO» №5 от 17 мая 2005 года)

15. Шеннон К. Работы по теории информации и кибернетике. - М.: ИЛ, 1963.

16. В. Ковалевский, "Криптографические методы", Компьютер Пресс 05.93 г.

17. С. Воробьев, "Защита инфор
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...