Среднеквадратичная скорость

Коэффициент

D=1/3<λ><V>

3. Коэффициент вязкости. Импульс молекул, находящихся слева от площадки, связанный с направленным движением слоёв газа, равен m₀v₁; справа- m₀v₂ Результирущий перенос.

 

Для газа < >= < >=

 

4. Коэффициент теплопроводности. Средняя энергия теплового движения молекул, находящихся слева от площадки, равна <E₁>=(i/2)k*T₁ справа<E₂>=(i/2)k*T₂

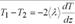
Теплопроводность λ численно равна плотности теплового потока при градиенте температуры равном единице.

Можно показать, что:

 

5. Законы идеал-ого газа: число молекул (атомов), равное числу Авогадро N _A = 6,022 *10²³ моль⁻¹.):

,

,так как масса газа m=m₀*N,

где m₀ – масса одной молекулы, N – число молекул; и по закону Авогадро: концентрация молекул, по определению, – число молекул в единице объёма: ,

а отношение двух констант – универсальной газовой и числа Авогадро – даёт постоянную Больцмана: =1,38*10^-23

Закон Дальтона: давление смеси газов равно сумме парциальных давлений всех входящих в смесь газов (6.10). Парциальное давление – это давление, которое оказывал бы данный газ в отсутствие других газов при тех же условиях.

По закону Паскаля давление в любой точке покоящегося газа или жидкости одинаково по всем направлениям и одинаково передаётся по всему объёму.

 

 

6. Уравнение Менделеева-Клапейрона. Оно является уравнением состояния идеального газа.

Идеальный - достаточно разреженный газ при не слишком низких температурах. Газ является идеальным, если:1) Собственным объёмом молекул можно пренебречь по сравнению с объёмом сосуда. 2) Взаимодействием молекул между собой можно пренебречь. Столкновения молекул между собой и со стенками сосуда – абсолютно упругие.
1) Закон Бойля-Мариотта. При постоянной температуре (изотермический процесс): ,

2) Закон Гей-Люссака. При постоянном давлении (изобарический процесс): ,

3) Закон Шарля. При постоянном объёме (изохорический процесс):

. ,

это уравнение Менделеева-Клапейрона. Оно является уравнением состояния идеального газа.

 

7. Основное уравнение МКТ: где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул ( в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.
Пусть имеется кубический сосуд с ребром длиной и одна частица массой в нём. Обозначим скорость движения , тогда перед столкновением со стенкой сосуда импульс частицы равен , а после — , поэтому стенке передается импульс . Время, через которое частица сталкивается с одной и той же стенкой, равно Отсюда следует:
Так как давление , следовательно Подставив, получим: Преобразовав: . Так как рассматривается кубический сосуд, то Отсюда: Соответственно, и 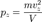. Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z.
Поскольку , то . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны. Отсюда 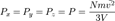или . Пусть — среднее значение кинетической энергии всех молекул, тогда: , откуда, используя то, что (количество вещества), а , имеем

 

 

9. Опыт Штерна

Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт явился одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям. Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего атомы начинали испаряться и летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью v, соответствующей подаваемому на концы нити напряжению. Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее. Стенки цилиндров специально охлаждались, что способствовало «оседанию» попадающих на них атомов. В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щёли малого цилиндра. Затем всю систему начинали вращать с некой достаточно большой угловой скоростью ω. При этом полоса налёта смещалась в сторону, противоположенную направлению вращения, и теряла чёткость. Измерив смещение s наиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул: , где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра. Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее   10.

10) Распределение Максвела. Наиболее вероятная скорость наиболее вероятная скорость, — вероятность обладания
которой любой молекулой системы максимальна, и которая соответствует максимальному значению . Чтобы найти её, необходимо вычислить , приравнять её нулю и решить относительно :

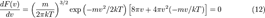
Средняя скорость

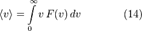
Подставляя и интегрируя, мы получим

Среднеквадратичная скорость

Подставляя и интегрируя, мы получим

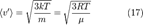
Распределение по энергии

Наконец, используя соотношения и , мы получаем распределение по кинетической энергии:

 

11. Барометрическая формула

 

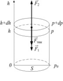Рассмотрим вертикальный столб газа с площадью основания (рис.6.12). Давление на высоте обозначим ; на высоте 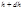давление равно (очевидно, ). На слой толщиной и массой , находящийся в равновесии, действуют силы:

1) – сила тяжести, её величину можно выразить через плотность газа и объём слоя : ;

2) – сила давления на высоте , направлена сверху вниз;

3) – сила давления на высоте 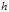, направлена снизу вверх. Слой находится в равновесии, то есть силы, действующие на него, уравновешивают друг друга:

,

Тогда .

Далее, после сокращения: .

Газ – идеальный; запишем уравнение Менделеева-Клапейрона: , тогда из .

Последнее уравнение проинтегрируем по высоте, учтя, что 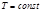и :

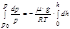
дальше

Поскольку то

Это – барометрическая формула, показывающая, как давление уменьшается с высотой в поле силы тяжести.

 

 

12. Распределение Больцмана.

Для идеального газа , , а произведение – потенциальная энергия молекулы в поле силы тяжести, то

. Полученное для молекул в однородном поле силы тяжести распределение Больцмана (6.55) универсально: годится для частиц, находящихся в любом потенциальном поле. Из (6.55) найдём отношение концентраций и частиц в двух точках 1 и 2:

.

Величина показывает, во сколько раз отличаются концентрации частиц в двух точках потенциального поля, если их потенциальные энергии отличаются на . Знак «минус» в (6.56) означает, что концентрация больше в тех точках, где потенциальная энергия меньше: всякая система с большей вероятностью будет находится в состоянии с наименьшей потенциальной энергией.

Последняя формула – это распределение частиц по координатам, потому что потенциальная энергия зависит от координат частицы: .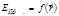

13. Число степеней свободы. Определение. Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы в пространстве.

а) Так, положение в пространстве материальной точки полностью определяется заданием трёх её координат (например, декартовых x, y, z или сферических, т.е. число степеней свободы i=3).

б) Система из 2-х жёстко связанных материальных точек (отрезок, их соединяющий, фиксирован). Координаты этих 2-х точек связаны соотношением ,, при этом достаточно задать 5 координат, а шестую можно найти из приведённого соотношения, т.е. i=5. Если точки не связаны между собой жёстко, то число степеней свободы i=6. Изменение даёт ещё одну степень свободы, которая называется колебательной.

Положение системы, состоящей из 2-х жёстко связанных материальных точек (или, например, стержня) можно задать следующим образом: задать 3 координаты центра инерции системы С и 2 угла и , которыми определяется направление в пространстве оси системы

Первые три степени свободы называется поступательными, а две другие – вращательными. Вращательные степени свободы соответствуют вращению вокруг 2-х взаимно перпендикулярных осей (всего i =5). в) Положение абсолютно твёрдого тела можно определить, задав 3 координаты центра инерции (поступательные степени свободы) и 3 угла (вращательные степени свободы). Т.е.i=6

 

14. Понятие внутренней энергии идеального газа

Определение. Внутренней энергией какого-либо тела называется энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Для идеального газа внутренняя энергия состоит из суммы энергий поступательного, вращательного и колебательного движений молекул.

Вся внутренняя энергия идеального газа определяется кинетической энергией беспорядочного движения его молекул.
Внутреннюю энергию одного моля идеального газа найдём, умножив число Авогадро на среднюю энергию одной молекулы:

Учитывая, что , получим:

внутренняя энергия идеального газа является функцией температурыи пропорциональна ей, а также зависит от числа степеней свободы молекул.

Изменение внутренней энергии идеального газа равно , т.е. определяется температурами начального и конечного состояний газа и не зависит от процесса.

16. Первое начало термодинамики. Все частные случаи. Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики^[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется. Рассмотрим несколько частных случаев: Если , то это означает, что тепло к системе подводится.
Если , аналогично — тепло отводится.
Если , то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

 

17. уравнением Майера
Для любого идеального газа справедливо соотношение Майера: , где — универсальная газовая постоянная, — молярная теплоёмкость при постоянном давлении, — молярная теплоёмкость при постоянном объёме. Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарному процессу в идеальном газе: ,

18. Адиаба́тный проце́сс — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством где — давление газа, — малое приращение объёма.

19. Тепловые и холодильные машины. Второй закон термодинамики. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).

 

20. Обратимые и необратимые процессы

Процесс наз. обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежут. состояний, что и в прямом процессе, но проходимую в обратном порядке. При этом в исходное состояние возвращается не только система, но и среда. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно. При этом предполагается, что равновесие существует между отдельными частями рассматриваемой системы и на границе с окружающей средой. Обратимый процесс - идеализир. случай, достижимый лишь при бесконечно медленном изменении термодинамич. параметров. Скорость установления равновесия должна быть больше, чем скорость рассматриваемого процесса. Если невозможно найти способ вернуть и систему, и тела в окружающей среде в исходное состояние, процесс изменения состояния системы наз. необратимым.

 

21. Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении. Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

 

 

22. неравенством Клаузиуса Энтропия замкнутой системы не убывает: причём для обратимых процессов и для необратимых.

Соотношение называется неравенством Клаузиуса и представляет собой одну из формулировок второго начала термодинамики: энтропия замкнутой системы остаётся постоянной, если в ней происходят только обратимые процессы, и возрастает в случае необратимых процессов.

вывод:

23. Энтропия. Термодинамич состояния системы. Изменение энтропии термодинамической системы при обратимом процессе это отношение общего количества тепла к величине абсолютной температуры (то есть тепло, переданное системе, при постоянной температуре): .

24.Второе начало термодинамики, определяющее направление тепловых процессов в изолированных системах: При любых происходящих в изолированной системе тепловых процессах система стремится к равновесному состоянию, при этом энтропия системы возрастает и достигает максимального значения в тепловом равновесии.Или: В изолированной системе энтропия не убывает

24.Второе начало термодинамики, определяющее направление тепловых процессов в изолированных системах: При любых происходящих в изолированной системе тепловых процессах система стремится к равновесному состоянию, при этом энтропия системы возрастает и достигает максимального значения в тепловом равновесии.Или: В изолированной системе энтропия не убывает

Поделиться:

Воспользуйтесь поиском по сайту: