Мнемонические правила для запоминания тригонометрических формул

 

(Из опыта работы)

 

При изучении темы «Тригонометрия» учащиеся сталкиваются с проблемой запоминания большого количества тригонометрических формул. Твердо знать эти формулы совершенно необходимо для дальнейшего изучения курса алгебры. Как лучше запомнить тригонометрические формулы с наименьшей нагрузкой на механическую память?

 

1. Знаки тригонометрических функций

Важно помнить, что

· все тригонометрические функции в I четверти принимают положительные значения (знак «+»);

· у синуса знаки расположены горизонтально,

· у косинуса – вертикально, а

· у тангенса и котангенса – крест-накрест.

Учащиеся прекрасно запоминают, что у тангенса и котангенса знаки располагаются крест-накрест, но забывают, у какой функции (синуса или косинуса), знаки расположены горизонтально, а у какой – вертикально. В этом случае поможет следующее правило: произносить слова «синус» и «косинус» нужно нараспев, выделяя ударную гласную и фиксируя при этом, в каком направлении вытягивается рот. При произнесении слова «синус» ударная гласная «и» вытягивает рот в направлении «↔», значит, у синуса знаки расположены горизонтально. Аналогично, при произнесении слова «косинус», ударная гласная «о» вытягивает рот в направлении «↕», значит, у косинуса знаки расположены вертикально.

 

2. Значения тригонометрических функций некоторых углов

Часто возникает путаница при использовании значений тригонометрических функций для углов 30°, 45° и 60°. Это происходит из-за существования некоторой симметрии в значениях функций данных углов. Значения тригонометрических функций для углов 30°, 45° и 60° следует запоминать следующим образом.

 

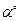
1. Сначала нужно составить таблицу, в первой строке которой следует записать по возрастанию 30°, 45° и 60°, а в первом столбце – функции по порядку: sin α, cos α, tg α и ctg α. Далее нужно запомнить всего одну клетку из всей таблицы, а именно, что , и заполнить ее.

 

 

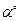
2. Затем приписать к единице знак радикала (карандашом). Получили «корень из одного пополам».

 

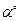
3. Далее в этой же строке заполняем две оставшиеся клетки, в некотором смысле по возрастанию: «корень из двух пополам» и «корень из трех пополам».

 

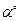
4. Вторую строку таблицы заполняем в обратном порядке. Таким образом, две строки таблицы полностью заполнены.

 

5. Учитывая формулу и выполняя соответствующее деление, заполняем третью строку таблицы; четвертую строку заполняем, как третью, но в обратном порядке.

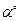
Получаем таблицу значений тригонометрических функций для углов 30°, 45° и 60°.

 

Понимая, как устроена таблица, учащиеся с легкостью запоминают ее.

 

3. Формулы приведения

Для запоминания этих формул необходимо знать два коротких правила:

1. Четверть дает знак.

2. Диаметр дает функцию.

Рассмотрим, например, как найти значение выражения . Сначала следует выполнить подготовительный момент: представить данное выражение в виде

1) 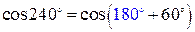, либо в виде

2) .

Предположим, что мы выбрали первый из представленных видов. Тогда, применяя первое правило, получим, что в III четверти косинус отрицательный (ставим знак «минус»). Далее задаем вопрос: «Меняем или не меняем функцию?». 180° попадают на горизонтальный диаметр. Помотав головой вдоль этого диаметра, получаем ответ: «Нет, не меняем». Получим

.

Теперь предположим, что мы выбрали второй из представленных видов. Вопрос со знаком решается аналогично – ставим знак «минус». А задавая вопрос: «Меняем или не меняем функцию?» и помотав головой вдоль соответствующего диаметра, получаем ответ: «Да, меняем», так как 270° попадают на вертикальный диаметр. Получим

.

 

4. Формулы понижения степени

,

.

 

Важно понять структуру этих формул, в частности, такой момент – «степень понижается, а угол становится в два раза больше». Эти формулы очень похожи друг на друга, поэтому для лучшего их запоминания следует применять правило: «Единица минус – дает синус, а единица плюс – дает косину́с».

 

5. Функция косинус

Про функцию косинус следует помнить, что она «четная, семейственная и отличная (от других)». Эти эпитеты позволяют запомнить многие тригонометрические формулы: четность/нечетность тригонометрических функций, формулы сложения, формулы преобразования суммы в произведение, а также формулы преобразования произведения в сумму.

Некоторую «семейственность», свойственную косинусу, можно проследить на примере формул сложения, формул преобразования суммы в произведение, а также формул преобразования произведения в сумму. И в каждом блоке этих формул можно уловить некую «отличительность», свойственную косинусу.

Формулы для ОДАРЕННЫХ

Тригонометрия	Периодичность
– основное тригонометрическое тождество

Формулы приведения

							Четность/нечетность

Значения тригонометрических функций некоторых угловДополнительные углы

, рад
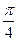
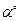
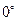
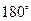
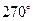
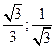
					не опр.		не опр.
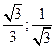
	не опр.					не опр.

Формулы двойного угла

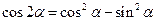
Формулы понижения степени

 

Формулы сложения
– синус суммы	– косинус суммы
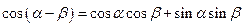– синус разности	– косинус разности
Формулы преобразования суммы в произведение	Формулы преобразования произведения в сумму
– сумма синусов
– разность синусов
– сумма косинусов
– разность косинусов

 

Поделиться:

Воспользуйтесь поиском по сайту: