Метод потенциалов. 2 версия ответа.

Вопрос 24 Алгоpитм pешения тpанспоpтной задачи методом потенциалов.

После построения начального опорного плана ТЗ возникает вопрос: как опреде-лить, будет ли построенный план оптимальным? Чтобы ответить на этот вопрос, необхо-димо знать признак оптимальности. Для этого разработан метод потенциалов, который опирается на теорему о потенциалах.

Каждому поставщику (ограничению по запасам) поставим в соответствие число , а каждому потребителю (ограничения по спросу) – число . Числа и называются потенциалами соответственно i -го поставщика и j -го потребителя.

Следующую теорему о потенциалах примем без доказательства.

 

Теорема 17.2. (теорема о потенциалах).

Если план 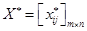транспортной задачи является оптимальным, то ему соот-ветствует система из 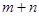чисел , удовлетворяющих условиям для и для .

 

Из теоремы следует, что для оптимального плана ТЗ необходимо выполнение условий:

1) каждой занятой клетке в распределительной таблице соответствует сумма потенциалов, равная тарифу этой клетки, т.е. ;

2) каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа этой клетки, т.е. .

Каждому поставщику поставим в соответствие некоторый потенциал α _i, а каждому потребителю – потенциал β _j (см. таблицу 2.5.5.).

Таблица 2.5.5

Оптимизация плана перевозок методом потенциалов

 

Присвоим любому потенциалу произвольное значение, например α₃=0. Остальные потенциалы легко определяются из условия, что для любой занятой клетки

α _i + β _j= Z _ij

Для каждой свободной клетки вычислим псевдостоимость

P _ij= α _i + β _j

и разность между стоимостью и псевдостоимостью

Δ _ij= Z _ij – P _ij

Запишем псевдостоимость в левых нижних уголках свободных клеток, а разность в кружках. Сравнивая эти разности с результатами, полученными в предыдущем разделе, убеждаемся, что эти разности характеризуют оценки соответствующих циклов.

Для клетки с наибольшей по модулю отрицательной разностью составляется единственный цикл, по которому и производится перестановка.

Перестановки могут осуществляться и сразу по нескольким циклам, но только в том случае, если они охватывают разные клетки.

По циклам, как и ранее, переставляется минимальное количество грузов, стоящее в отрицательных клетках.

Процедура повторяется до тех пор, пока есть отрицательные циклы.

 

Метод потенциалов. 2 версия ответа.

 

Согласно теореме о потенциалах, каждой занятой клетке будет соответствовать уравнение . Так как всех занятых клеток должно быть 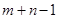, т.е. на единицу меньше, то для определения чисел и , необходимо решить систему из 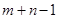урав-нений с 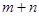неизвестными. Система неопределенная, и, чтобы найти част-ные решения, одному из потенциалов придается произвольной числовое значение, тогда остальные потенциалы определятся однозначно. Для облегчения расчетов одному из по-тенциалов придается обычно значение, равное нулю.

Для исследования плана на оптимальность по каждой свободной клетке прове-ряется условие . Если хотя бы одна свободная не удовлетворяет данному усло-вию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т.е.

.

Если для всех свободных клеток оценки , то опорный план перевозок явля-ется оптимальным. Если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загрузки свободной клетки с отрицательной оценкой план перевозки улучшается. Для наиболее перспективной свободной клетки строится замк-нутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно припи-сываются знаки: свободной клетке – знак «+», следующей по часовой или против часовой стрелки занятой клетке – знак «-», следующей – снова «+» и т.д. Из поставок в клетках цикла с «отрицательными» вершинами выбирается наименьшее количество l груза, ко-торое и перемещается по клеткам этого цикла: прибавляется к поставкам в положи-тельных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушается.

В общем случае цикл представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки строки (столбца). Цикл включает одну свободную клетку, остальные клетки цикла заняты. В цикле всегда четное число клеток. Для свободной клетки всегда можно построить единственный цикл. Если из занятых клеток образуется цикл, то план перевозок не является опорным. Цикл строится лишь для свободных клеток.

 

Сформулируем алгоритм решения ТЗ методом потенциалов:

1) построить опорный план;

2) вычислить потенциалы поставщиков и потребителей и , решив систему уравнений вида ;

3) вычислить оценки для всех свободных клеток по формуле . Если , то полученный план является оптимальным. При этом если все , то по-лученный оптимальный план единственный. В случае, если хотя бы одна оценка , имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции.

Пример 17.1. В пунктах производится однородная продукция в коли-чествах единиц. Готовая продукция поставляется в пункты , потребности которых составляют единиц. Стоимость c_ij перевозки единицы продукции из пункта A_i в пункт B_j заданы матрицей :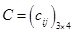

.

Требуется:

1) методом потенциалов найти план перевозок продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям;

2) вычислить суммарные затраты f_min.

 

Решение.

1) Найдем суммарные запасы продукции и суммарные потребности 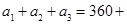150+380=890; b ₁+ b ₂+ b ₃+ b ₄=270+190+340+200=1000. Поскольку ,то есть отсутствует баланс между производимой продукцией и потребнос-тями, то мы имеем задачу открытого типа. Вводим фиктивного поставщика A ₄, который имеет запас продукции в объеме (един.). Все тарифы на доставку продукции фиктивного поставщика равны нулю, т.е. c ₄₁= c ₄₂= c ₄₃= c ₄₄=0

Данные задачи заносим в таблицу 1.

Табл. 1.

Поставщики	Потребители	Запас груза, ai
B 1	B 2	B 3	B 4
A 1
A 2
A 3
A 4
Потребность в грузе, bj

 

Начальный опорный план получим по правилу «минимального элемента».

Загрузку начинаем с клетки, которой соответствует наименьший тариф c_ij ≠0 всей матрицы тарифов. В нашем случае минимальным тарифом является с ₁₄=1, который соот-ветствует клетке (1, 4). В эту клетку вписываем x ₁₄=min (360; 200)=200. Исключаем четвертый столбец. У поставщика A ₁ осталось еще 160 единиц продукции, которые по-местим в клетку (1, 2). Исключаем первую строку. Но потребителю B ₂ необходимо еще 30 ед. продукции, которые берем у поставщика A ₂, и помещаем в клетку (2, 3). Исключаем второй столбец. Оставшиеся у поставщика A ₂ 120 ед. продукции помещаем в клетку (2, 3). Исключаем вторую строку. Необходимые потребителю B ₃ 220 ед. продукции берем у поставщика A ₃ и помещаем в клетку (3, 3). Исключаем третий столбец. В пункте A ₃ оставшиеся 160 ед. продукции помещаем в клетку (3; 1). Исключаем третий столбец. Оставшиеся 110 ед. помещаем в клетку (4; 1).

Полученный нами план является невырожденным, так как выполняется условие базисных клеток: m + n -1=4+4-1=7, и число заполненных клеток тоже 7. А значит, полу-чено опорное решение, которое запишем матрицей

.

 

Методом потенциалов проверим, является ли полученное решение оптимальным. Для этого каждому поставщику и потребителю придается число, называемое потен-циалом. Потенциалы выбираем так, чтобы их сумма для каждой загруженной клетки была равна тарифу перевозки единицы груза, т.е.

u_i+v_j=c_ij,

где u_i – потенциал i -го поставщика;

v_j – потенциал j -го потребителя;

c_ij – тариф заполненной клетки.

В нашем случае получаем следующие уравнения:

Полагая v ₄=0, получаем следующие потенциалы:

u ₁=1 u ₃=3 v ₁= 0 v ₃= 4

u ₂=0 u ₄=0 v ₂= 2 v ₄=0

 

Все полученные данные заносим в таблицу 2.

Далее вычисляем оценки свободных клеток по формуле: .

s ₁₁= c ₁₁-(u ₁+ v ₁) =7-(1+0) =6 ³ 0 s ₂₄= c ₂₄-(u ₂+ v ₄) = 8-(0+0) =8 ³ 0 s ₄₂= c ₄₂-(u ₄+ v ₂) = 0-(0+2) = -2

s ₁₃= c ₁₃-(u ₁+ v ₃) = 6-(1+4) =1 ³ 0 s ₃₂= c ₃₂-(u ₃+ v ₂) = 5-(3+2) = 0 s ₄₃= c ₄₃-(u ₄+ v ₃) = 0-(0+4) = -4

s ₂₁= c ₂₁-(u ₂+ v ₁) = 5-(0+0) =5 ³ 0 s ₃₄= c ₃₄-(u ₃+ v ₄) = 9-(3+0) = 6 ³ 0 s ₄₄= c ₄₄-(u ₄+ v ₄) = 0-(0+0) = 0

Так как s ₄₂<0, и s ₄₃<0 то полученный план не является оптимальным. Наиболее потенциальной клеткой является клетка (4; 3). Поэтому строим для клетки (4; 3) замк-нутый цикл, который в таблице 2 выделяем пунктирной линией:

(4, 3)→(3, 3)→(3, 1)→(4, 1).

Свободной клетке условно приписываем знак «+», тогда следующей клетке по ходу часовой стрелки – знак «-» и т.д., знаки чередуются.

В отрицательных вершинах цикла определяем наименьшую загрузку клетки, т.е.

min (x ₃₃, x ₄₁)=min (220, 110)=110.

Количество продукции, равное 110ед., прибавляем к поставкам в клетках со знаком «+» и вычитаем из поставок в клетках со знаком «-».

Получаем новый план, который заносим в таблицу 3.

Проверяем, является ли полученный план оптимальным. Для этого каждому поставщику и потребителю придаем число – потенциал. Вычисляем потенциалы так же, как это делали выше:

.

Полагая v ₃=0, получаем следующие потенциалы, которые заносим в таблицу 4:

u ₁=5 u ₃=7 v ₁= -4 v ₃= 0

u ₂=4 u ₄=0 v ₂= -2 v ₄= -4

Вычисляем оценки свободных клеток:

s ₁₁=7-(5-4) =6 ³ 0 s ₂₄=8-(4-4) = 8 ³ 0 s ₄₁=0-(0-4) = 4 ³ 0

s ₁₃=6-(5+0) =1 ³ 0 s ₃₂=5-(7-2) = 0 s ₄₂=0-(0-2) =2 ³ 0

s ₂₁=5-(4-4) =5 ³ 0 s ₃₄=9-(7-4) = 6 ³ 0 s ₄₄=0-(0-4) = 4 ³ 0

 

Поскольку все s_ij> 0, то полученный план является оптимальным, который можно представить в виде матрицы

.

 

2) Суммарные затраты f _min при этом будут составлять:

Потребитель B ₃ не дополучил 110 единиц продукции.

Ответ: , f _min=2800 ден.ед.

 

Поделиться:

Воспользуйтесь поиском по сайту: