 |
Измерить тесноту связи между указанными признаками
|
|
|
|
КУРСОВАЯ РАБОТА
По статистике
«Статистические методы выявления взаимосвязей общественных явлений»
Выполнила:
Проверила:
Москва, 2006г.
План.
Содержание:
Введение. 3
Виды и методы взаимосвязи. 4
Виды взаимосвязи.. 4
Методы взаимосвязи.. 5
1. Аналитические группировки. 5
2. Метод параллельных рядов. 6
3. Балансовый метод. 7
4. Корреляционно-регрессионный анализ. 7
Практическая часть.. 16
Аналитическая часть.. 24
Заключение.. 30
Список литературы... 31
Введение.
Все явления и процессы, протекающие в экономике любой страны взаимосвязаны между собой. Cстатистическое изучение этой взаимосвязи имеет особо важное значение в связи с тем, что оно позволяет выявить закономерности развития и осуществить прогнозирование этих явлений и процессов.
Каждый процесс и явление можно рассматривать с двух сторон. С первой стороны они испытывают влияние других явлений и процессов и выступают как результат этого влияния. С другой стороны каждое явление в свою очередь выступает как фактор, оказывающий влияние на другие явления и процессы. Поэтому признаки, которые испытывают влияние, называются результативными; признаки, которые оказывают влияние - факторные.
Результативные признаки обозначаются через Y, факторные через X. Поэтому в общем виде взаимосвязь между результатом и факторами можно записать формулой:
fy =(x1,x2 …)
следовательно Y является функцией от всех X.
Если на результат оказывает влияние первый фактор, то в этом случае изучается корреляция и регрессия, которые носят название парных; если на результат оказывает влияние несколько факторов, то изучается множественная корреляция и множественная регрессия.
|
|
|
Важной задачей статистики является разработка методики статистической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки.
Но, исследуя явления в самых различных областях, статистика сталкивается с зависимостями, как между количественными, так и между качественными показателями, признаками. При этом задача статистики – обнаружить (выявить) такие зависимости и дать их количественную характеристику.
Как правило, анализ социальных явлений, их связей и зависимостей должен начинаться с построения графиков связей. В настоящее время используются графики, характеризующие связь социальных явлений (рис.1).
 |
а)
Б) в)
Рис.1 Графики, характеризующие связь социальных явлений
С помощью графика (рис.1.а) «цепь» изображаются связи между социальными признаками, которые одинаково существенны и значимы.
График (рис.1.б) «звезда» изображают зависимость социальных явлений, которые тяготеют к одному наиболее значимому. Исключение данного признака нарушает взаимосвязи между оставшимися признаками.
На графике (рис.1.в) «сетка» выделяется несколько значимых признаков, которые тесно зависимы друг от друга.
Виды и методы взаимосвязи.
Виды взаимосвязи
Статистика различает следующие виды взаимосвязи:
1. Функциональная и статистическая. Первый вид взаимосвязи имеет место тогда, когда первому значению фактора соответствует одно или несколько четко определенных значений результата. Например, S=Vt. Статистическая взаимосвязь имеет место тогда, если каждому значению фактора соответствует неопределенное множество значений результата. Статистика изучает только статистические связи.
2. Прямая и обратная. Прямая наблюдается в том случае, если движение фактора и результата направлены в одну сторону; обратная связь имеет место, если их движение противоположны.
|
|
|
3. Прямолинейная и криволинейная взаимосвязи. Прямолинейная выражается формулой уравнения прямой у = а + bx; криволинейная выражается уравнением параболы, гиперболы и других кривых y = x2 + bx + c.
В экономической практике не встречаются взаимосвязи, которые полностью можно описать при помощи формальных уравнений. Поэтому при характере взаимосвязи задачи статистики заключаются в следующем:
1) определить вид и характер взаимосвязи;
2) подобрать теоретическую функцию, которая наиболее точно описывает взаимосвязь фактора и результата. Это дает возможность прогнозировать результат показателя на основании прогноза факторов.
Методы взаимосвязи
Статистика изучает взаимосвязи при помощи системы методов, важнейшими среди которых являются:
1. Аналитические группировки, где факторный признак располагается по убыванию или возрастанию, а в соответствии с этим располагается и результативный признак. это дает возможность визуальным путем определить характер и тесноту взаимосвязи. Например, распределение по весу в зависимости от возраста.
| Возраст | Вес |
| 0 | 3,5 |
| 1 | 5,7 |
| 2 | 9,2 |
| 3 | 13,4 |
| 4 | 17,7 |
2. Метод параллельных рядов. Строятся два ряда признаков, которые находятся в определенной взаимосвязи; затем визуально определяют характер и тесноту взаимосвязи. Например, данные о численности занятых в ВВП.
| S занятых | ВВП, млрд.руб |
| 150 | 30 |
| 200 | 32 |
| 170 | 35 |
| 190 | 28 |
| 220 | 37 |
Для характеристики взаимосвязи факторный признак располагают в монотонно убывающем или возрастающем порядке, а показатели результата перемещаются в соответствии с факторным показателем.
| S занятых | ВВП, млрд.руб |
| 150 | 30 |
| 170 | 35 |
| 190 | 28 |
| 200 | 32 |
| 220 | 37 |
3. Балансовый метод широко применяется в экономике. Основной показатель развития ВВП проходит в своем движении 3 стадии: производство, распределение и перераспределение, конечное использование.
Взаимосвязь между отдельными стадиями движения ВВП и отдельными компонентами ВВП осуществляется при помощи балансового метода. Его суть заключается в том, что величина ВВП на всех трех стадиях должна быть одинакова.
|
|
|
Основными методами изучения взаимосвязи социально-экономических явлений служат равные коэффициенты и корреляционно-регрессионный анализ.
4. Корреляционно-регрессионный анализ. Корреляционная связь – связь, проявляющаяся при достаточно большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами.
Изучение корреляционных связей сводится в основном к решению следующих задач:
Ø выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками. Эта задача может быть решена на основе параллельного сопоставления (сравнения) значений х и у у n единиц совокупности; с помощью группировок; построения и анализа специальных корреляционных таблиц; а также построения диаграмм рассеяния;
Ø измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов. Эта часть исследования называется корреляционный анализ;
Ø определение уравнения регрессии – математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных – факторных признаков. Эта часть исследования называется регрессионный анализ.
Задача корреляционного анализа – измерение тесноты связи между варьируемыми признаками и оценка факторов, оказывающих наибольшее влияние.
Задача регрессионного анализа – выбор типа модели (формы связи), устанавливающих степени влияния независимых переменных.
Связь признаков проявляется в их согласованной вариации, при этом одни признаки выступают как факторные, а другие – как результативные. Причинно-следственная связь факторных и результативных признаков характеризуется по степени:
· тесноты;
· направлению;
· аналитическому выражению.
4.1. Регрессионный анализ. Для оценки параметров уравнений регрессии наиболее часто используется метод наименьших квадратов (МНК), суть которого заключается в следующем требовании: искомые теоретические значения результативного признака  должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических (фактических) значений, т.е.
должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических (фактических) значений, т.е.
|
|
|
 . (6.1)
. (6.1)
При изучении связей показателей применяются различного вида уравнения прямолинейной и криволинейной связи. Так, при анализе прямолинейной зависимости применяется уравнение:
 (6.2)
(6.2)
При криволинейной зависимости применяется ряд математических функций:
полулогарифмическая  (6.3)
(6.3)
показательная  (6.4)
(6.4)
степенная 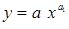 (6.5)
(6.5)
параболическая 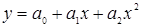 (6.6)
(6.6)
гиперболическая 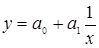 (6.7)
(6.7)
Наиболее часто используемая форма связи между коррелируемыми признаками – линейная, при парной корреляции выражается уравнением (6.2), где а 0 – среднее значение в точке x =0, поэтому экономической интерпретации коэффициента нет; а 1 – коэффициент регрессии, показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
Система нормальных уравнений МНК для линейной парной регрессии имеет следующий вид:
 (6.8)
(6.8)
Отсюда можно выразить коэффициенты регрессии:
 ;
;
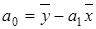 . (6.9)
. (6.9)
Для практического использования регрессионных моделей необходима проверка их адекватности. При численности объектов анализа до 30 единиц возникает необходимость проверить, насколько вычисленные параметры характерны для отображаемого комплекса условий, не являются ли полученные значения параметров результатом действия случайных причин. Значимость коэффициентов регрессии применительно к совокупности n <30 определяется с помощью t-критерия Стьюдента. При этом вычисляются фактические значения t-критерия:
для параметра а 0:  , (6.10)
, (6.10)
для параметра а 1:  . (6.11)
. (6.11)
В формулах (6.10) и (6.11):
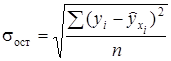 - среднее квадратическое отклонение результативного признака
- среднее квадратическое отклонение результативного признака  от выровненных значений
от выровненных значений  . (6.12)
. (6.12)
|
|
|
 - среднее квадратическое отклонение факторного признака
- среднее квадратическое отклонение факторного признака  от общей средней
от общей средней  . (6.13)
. (6.13)
Полученные по формулам (6.10) и (6.11) фактические значения  и
и  сравниваются с критическим
сравниваются с критическим  , который получают по таблице Стьюдента с учетом принятого уровня значимости
, который получают по таблице Стьюдента с учетом принятого уровня значимости  и числа степеней свободы ν(ν = n- k- 1, где n – число наблюдений, k – число факторов, включенных в уравнение регрессии). Рассчитанные параметры а 0 и а 1 уравнения регрессии признаются типичными, если t фактическое больше t критического.
и числа степеней свободы ν(ν = n- k- 1, где n – число наблюдений, k – число факторов, включенных в уравнение регрессии). Рассчитанные параметры а 0 и а 1 уравнения регрессии признаются типичными, если t фактическое больше t критического.
4.2. Корреляционный анализ позволяет установить тесноту связи между факторами и решить следующие задачи:
· ответить на вопрос: существует ли связь?
· выявить изменение связи в различных ситуациях реальных данных;
· определить наиболее значимые факторы в результативном признаке;
Различают:
· парную корреляцию – это зависимость между результативным и факторным признаком;
· частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;
· множественную – многофакторное влияние в статической модели  .
.
К простейшим показателям тесной связи относятся:
· линейный коэффициент корреляции К.Пирсона;
· коэффициент детерминации;
· коэффициенты корреляции знаков – для оценки тесноты связи качественных признаков (непараметрические методы), Г. Фехнера, К. Спирмэна, М. Кэндэла.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции, который рассчитывается по одной из формул:
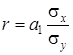 (6.16)
(6.16)
 . (6.17)
. (6.17)
а также
 или
или  .
.
Корреляционный анализ выполняет оценку адекватности регрессионной модели, но путем установления тесноты связи.
Оценка линейного коэффициента корреляции
| Значение r | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | Изменение x не влияет на изменения y |
| 0 < r < 1 | Прямая | С увеличением x увеличивается y |
| -1 > r > 0 | Обратная | С увеличением x уменьшается y и наоборот |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного |
Значимость линейного коэффициента корреляции проверяется на основе t- критерия Стьюдента. Для этого определяется фактическое значение критерия  :
:
 , (6.18)
, (6.18)
Вычисленное по формуле (6.18) значение  сравнивается с критическим
сравнивается с критическим  , который получают по таблице Стьюдента с учетом принятого уровня значимости
, который получают по таблице Стьюдента с учетом принятого уровня значимости  и числа степеней свободы ν.
и числа степеней свободы ν.
Коэффициент корреляции считается статистически значимым, если t расч превышает  (t расч >
(t расч >  ).
).
Универсальным показателем тесноты связи является теоретическое корреляционное отношение:
 , (6.19)
, (6.19)
где  – общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
– общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
 – факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
– факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
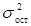 – остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
– остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
По правилу сложения дисперсий:
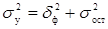 , т.е.
, т.е. 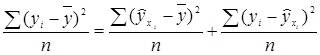 . (6.19)
. (6.19)
Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока)
Значение 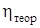
| Характер связи | Значение 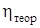
| Характер связи | |
| η = 0 | Отсутствует | 0,5 ≤ η < 0,7 | Заметная | |
| 0 < η < 0,2 | Очень слабая | 0,7 ≤ η < 0,9 | Сильная | |
| 0,2 ≤ η < 0,3 | Слабая | 0,9 ≤ η < 1 | Весьма сильная | |
| 0,3 ≤ η < 0,5 | Умеренная | η = 1 | Функциональная |
Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = | r|.
Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:
 , (6.20)
, (6.20)
где  – парные коэффициенты корреляции между признаками.
– парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен:  .
.
| Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками. |
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:
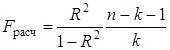 , (6.21)
, (6.21)
где R 2 – коэффициент множественной детерминации (R 2  );
);
k – число факторных признаков, включенных в уравнение регрессии.
Связь считается существенной, если F расч > F табл – табличного значения F- критерия для заданного уровня значимости α и числе степеней свободы ν1 = k,ν2 = n – k – 1.
Частные коэффициенты корреляции характеризуют степень тесноты связи результативного признака и фактора, при элиминировании его взаимосвязи с остальными факторами, включенными в анализ. В случае зависимости у от двух факторных признаков частные коэффициенты корреляции рассчитываются:
 ;
;  , (6.22)
, (6.22)
где r – парные коэффициенты корреляции между указанными в индексе переменными.
В первом случае исключено влияние факторного признака х 2, во втором – х 1.
Для оценки сравнительной силы влияния факторов, по каждому фактору рассчитывают частные коэффициенты эластичности:
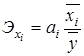 , (6.23)
, (6.23)
где  – среднее значение соответствующего факторного признака;
– среднее значение соответствующего факторного признака;
 – среднее значение результативного признака;
– среднее значение результативного признака;
 – коэффициент регрессии при i -м факторном признаке.
– коэффициент регрессии при i -м факторном признаке.
Данный коэффициент показывает, на сколько процентов следует ожидать изменения результативного показателя при изменении фактора на 1% и неизменном значении других факторов.
Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией i -го признака, входящего в множественное уравнение регрессии, рассчитывается по формуле:
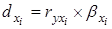 , (6.24)
, (6.24)
где  – парный коэффициент корреляции между результативным и i -м факторным признаком;
– парный коэффициент корреляции между результативным и i -м факторным признаком;
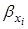 – соответствующий стандартизованный коэффициент уравнения множественной регрессии:
– соответствующий стандартизованный коэффициент уравнения множественной регрессии:
 . (6.25)
. (6.25)
Практическая часть
Выявить зависимость между нераспределенной прибылью и инвестициями в основные фонды, применяя:
А) метод параллельных рядов
Б) метод группировок
В) графический метод
Измерить тесноту связи между указанными признаками
Таблица№1
Для изучения капитальных вложений в производство из собственных средств предприятий в регионе проведена 5%-я механическая выборка, в результате которой получены следующие данные:
| № п/п | Нераспределенная прибыль, млн. руб. | Инвестиции в основные фонды, млн.руб. |
| А | 1 | 2 |
| 1 | 2,2 | 0,06 |
| 2 | 2,0 | 0,04 |
| 3 | 4,3 | 0,44 |
| 4 | 5,0 | 0,6 |
| 5 | 6,0 | 0,90 |
| 6 | 2,3 | 0,12 |
| 7 | 3,6 | 0,20 |
| 8 | 4,2 | 0,36 |
| 9 | 5,8 | 0,80 |
| 10 | 4,7 | 0,60 |
| 11 | 2,5 | 0,18 |
| 12 | 3,8 | 0,40 |
| 13 | 4,5 | 0,53 |
| 14 | 4,8 | 0,65 |
| 15 | 4,4 | 0,42 |
| 16 | 5,4 | 0,70 |
| 17 | 5,2 | 0,50 |
| 18 | 4,1 | 0,35 |
| 19 | 3,3 | 0,20 |
| 20 | 5,6 | 0,70 |
| 21 | 3,9 | 0,40 |
| 22 | 4,8 | 0,73 |
| 23 | 4,5 | 0,62 |
| 24 | 4,7 | 0,70 |
| 25 | 3,4 | 0,30 |
1. Метод параллельных рядов. Произведем ранжирование капитальных вложений в производство по нераспределенной прибыли
Таблица№2
| № п/п | Нераспределенная прибыль, млн. руб. | Инвестиции в основные фонды, млн.руб. |
| А | 1 | 2 |
| 1 | 2 | 0,04 |
| 2 | 2,2 | 0,06 |
| 3 | 2,3 | 0,12 |
| 4 | 2,5 | 0,18 |
| 5 | 3,3 | 0,2 |
| 6 | 3,4 | 0,3 |
| 7 | 3,6 | 0,2 |
| 8 | 3,8 | 0,4 |
| 9 | 3,9 | 0,4 |
| 10 | 4,1 | 0,35 |
| 11 | 4,2 | 0,36 |
| 12 | 4,3 | 0,44 |
| 13 | 4,4 | 0,42 |
| 14 | 4,5 | 0,53 |
| 15 | 4,5 | 0,62 |
| 16 | 4,7 | 0,6 |
| 17 | 4,7 | 0,7 |
| 18 | 4,8 | 0,65 |
| 19 | 4,8 | 0,73 |
| 20 | 5 | 0,6 |
| 21 | 5,2 | 0,5 |
| 22 | 5,4 | 0,7 |
| 23 | 5,6 | 0,7 |
| 24 | 5,8 | 0,8 |
| 25 | 6 | 0,9 |
После проведения ранжирования четко видна взаимосвязь нераспределенной прибыли от инвестиций в основные фонды. При большей прибыли инвестиции в основные фонды больше.
2. Метод группировок. Для образования групп предприятий по нераспределенной прибыли необходимо определить величину интервала по формуле Стерджесса:
I = x max - x min
n , где
х мах - наибольший показатель нераспределенной прибыли в млн. руб.
х min – наименьший показатель нераспределенной прибыли в млн. руб.
распределим предприятия по величине интервала, следовательно, величина интервала составит 0,8
I =(6-2)/5=0,8
Таблица№3.
Распределение предприятий по нераспределенной прибыли за отчетный период.
| № группы | Группы предприятий по нераспределенной прибыли, млн.руб. | Число предприятий | Удельный вес числа предприятий, % |
| А | Б | 1 | 2 |
| I | 2,0-2,8 | 4 | 16 |
| II | 2,8-3,6 | 3 | 12 |
| III | 3,6-4,4 | 6 | 24 |
| IV | 4,4-5,2 | 8 | 32 |
| V | 5,2-6,0 | 4 | 16 |
Итого


