 |
Независимость событий. Теорема умножения вероятностей
|
|
|
|
Основные теоремы теории вероятностей
Теорема сложения вероятностей
Вероятность суммы двух несовместных событий определяется аксиомой А3:
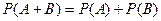 ,
, 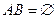 .
.
Выведем формулу вероятностей двух совместных событий.
Теорема 3.1. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения
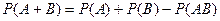 . .
| (3.1) |
Доказательство. Представим события 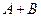 и В в виде суммы двух несовместных событий:
и В в виде суммы двух несовместных событий:  ,
, 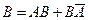 . В справедливости формул можно наглядно убедиться на рис.1.
. В справедливости формул можно наглядно убедиться на рис.1.

Рис. 1
Тогда согласно аксиоме А3, имеем:  и
и 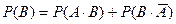 . Отсюда следует
. Отсюда следует 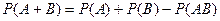 .
.
Формула (3.1) справедлива для любых событий А и В.
Можно получить формулу вероятности суммы трех и большего числа совместных событий. Для трех событий она имеет вид:
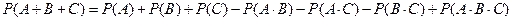 . .
| (3.2) |
Вероятность суммы нескольких совместных событий 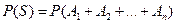 , можно найти, используя равенство
, можно найти, используя равенство 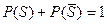 , где
, где 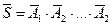 - противоположно событию S. Тогда
- противоположно событию S. Тогда  .
.
Пример 3.1. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?
Решение:
Введем события: А – появление шестерки на первой кости, В – появление шестерки на второй кости. Тогда А+В – появление хотя бы одной шестерки при бросании костей. События А и В совместные. По формуле (3.1) находим
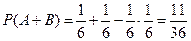 .
.
Иначе: 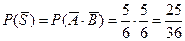 . Следовательно,
. Следовательно,  .
.
Условные вероятности
Пусть А и В – два события, рассматриваемые в данном опыте. Наступление одного события может влиять на возможность наступление другого. Для характеристики зависимости одних событий от других вводится понятие условной вероятности.
Условной вероятностью события В при условии, что произошло событие А, называется отношение вероятности произведения этих событий к вероятности события А, причем  , обозначается символом
, обозначается символом 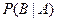 . Таким образом, по определению:
. Таким образом, по определению:
|
|
|
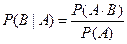 , ,  . .
| (3.3) |
Вероятность Р (В), в отличии от условной, называется безусловной вероятностью.
Аналогично определяется условная вероятность события А при условии В, т.е. 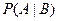 :
:
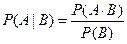 , , 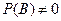 . .
| (3.4) |
Отметим, что условная вероятность, скажем 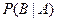 , удовлетворяет аксиомам Колмогорова:
, удовлетворяет аксиомам Колмогорова:
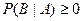 ,
,
 ,
,
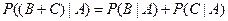 , если
, если  .
.
Поэтому для условной вероятности справедливы все свойства из аксиом.
Пример 3.2. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимают два шара. Какова вероятность того, что 2-й шар окажется белым при условии, что 1-й шар был черным?
Решение:
1-й способ. Пусть А – 1-й шар черный, В – 2-й шар белый. Так как событие А произошло, то в урне осталось 8 шаров, из которых 2 белых. Поэтому 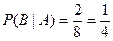 .
.
2-й способ. Найдем 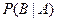 по формуле (3.3). очевидно, что
по формуле (3.3). очевидно, что 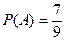 . Находим
. Находим 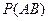 :
: 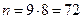 - общее число исходов (появление двух шаров). Событию АВ благоприятствуют
- общее число исходов (появление двух шаров). Событию АВ благоприятствуют  исходов. Поэтому
исходов. Поэтому  . Следовательно,
. Следовательно,
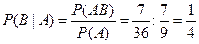 .
.
Независимость событий. Теорема умножения вероятностей
Из определения условной вероятности следует, что
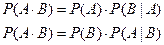 . .
| (3.5) |
т.е. вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
Равенство (3.5) называют правилом или теоремой умножения вероятностей. Это правило обобщается на случай n событий.
 . .
| (3.6) |
Для трех событий А1, А2, А3 получаем:
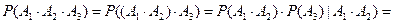
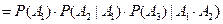 .
.
Правило умножения вероятностей имеет простой вид, если события, образующие произведение, независимы.
Событие А называется независимым от события В,если его условная вероятность равна безусловной, т.е. если выполняется равенство
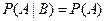 . .
| (3.7) |
Лемма 3.1 (о взаимной независимости событий). Если событие А не зависит от события В, то и событие В не зависит от события А.
Доказательство. Из равенства (3.5), с учетом равенства (3.7), следует
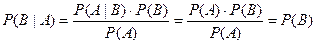 , т.е. , т.е. 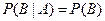 , ,
| (3.8) |
а это означает, что событие В не зависит от события А.
Можно дать следующее определение независимости событий.
|
|
|
Два, события называются независимыми, если появление одного из них не меняет вероятность появления другого.
Для независимых событий правило умножения вероятностей принимает вид:
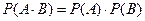 , ,
| (3.9) |
т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Равенство (3.9) часто используют в качестве определения независимости событий: события А и В называются независимыми, если 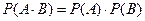 .
.
Можно показать, что если события А и В независимы, то независимы события  и В, А и
и В, А и 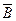 ,
,  и
и 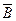 .
.
На практике о независимости тех или иных событий часто судят исходя из интуитивных соображений и анализа условий опыта, считая независимыми события, «между которыми нет причинно-следственных связей».
Понятие независимости может быть распространено на случай n событий.
События А 1, А 2,…, А n называются независимыми (или независимыми в совокупности), если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. В противном случае события А 1, А 2,…, А n называются зависимыми.
Для независимых событий их условные вероятности равны безусловным и формула (3.6) упрощается:
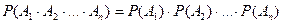 . .
| (3.10) |
Из попарной независимости событий А 1, А 2,…, А n (любые два из них независимы) не следует их независимость в совокупности (обратное верно).
Пример 3.3. Производится выбор флага из 4-х, имеющихся в наличии: красного, голубого, белого и трехцветного (красно-бело-голубого). Исследовать на независимость события: К – выбранный флаг имеет красный цвет, Г –голубой цвет, Б – белый.
Решение:
Возможных исходов выбора 4. Событию К благоприятствуют 2 исхода, т.к. красный имеется у двух флагов. Поэтому 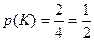 . Аналогично находим, что
. Аналогично находим, что 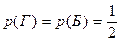 . Событию К∙Г – выбран флаг, имеющий 2 цвета (красный и голубой), - благоприятствует один исход. Поэтому,
. Событию К∙Г – выбран флаг, имеющий 2 цвета (красный и голубой), - благоприятствует один исход. Поэтому, 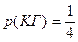 . И так как
. И так как  , т.е.
, т.е.  , то события К и Г независимы. Аналогично убеждаемся в независимости событий К и Б, Б и Г. Значит, события К, Б, Г попарно независимы. Но
, то события К и Г независимы. Аналогично убеждаемся в независимости событий К и Б, Б и Г. Значит, события К, Б, Г попарно независимы. Но 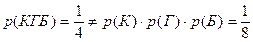 , следовательно события К, Г и Б не являются независимыми в совокупности.
, следовательно события К, Г и Б не являются независимыми в совокупности.
|
|
|


